Интервальное оценивание

Пусть имеется параметрическая ста­тистическая модель ( ), , и по выборке Z_n = = col(Х₁, ...,X_n), соответствующей распределению F(x,θ) наблю­даемой СВ X, требуется оценить неизвестный параметр θ. Вместо точечных оценок, рассмотренных ранее, рассмотрим другой тип оце­нок неизвестного параметра .

Определение 3.8. Интервал 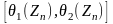со случайными концами, «накрывающий» с вероятностью 1 — а, 0 < а < 1, неиз­вестный параметр θ,

т. е.

,

называется доверительным интервалом (или интервальной оценкой) уровня надежности 1 - а параметра θ.

Определение 3.9. Число называется доверитель­ной вероятностью или уровнем доверия (надежности).

Определение 3.10. Доверительный интервал называется центральным, если выполняются следующие условия:

Часто вместо двусторонних доверительных интервалов рассматри­вают односторонние доверительные интервалы, полагая или .

Определение 3.11. Интервал, границы которого удовлетворя­ют условию:

(или ),

называется соответственно правосторонним (или левосторонним) доверительным интервалом.

Проверка гипотезы о виде закона распределения

Пусть имеется реализация zn выборки Zn порожденной СВ Xс неизвестной функцией распределения F(x).Требуется проверить гипотезу H0, состоящую в том, что СВ X имеет определенный закон распределения F−(x,θ)   (например, нормальный, равномерный и т.д.). Истинный закон распределения F(x)   неизвестен. Для проверки такой гипотезы можно использовать статистический критерий хи-квадрат (критерий Пирсона).

Правило проверки заключается в следующем.

1) Формулируется гипотеза H0, состоящая в том, что СВ X имеет распределение определенного вида F−(x,θ1,...,θs)   с s   неизвестными параметрами θ1,...,θs   (например, m и σ2   для нормального распределения, a и b   — для равномерного и т.д.).

2) По реализации zn   выборки Zn методом максимального правдоподобия находятся оценки θˆ1,...,θˆs неизвестных параметров θ1,...,θs.

3) Действительная ось ℝ1   разбивается на l+1   непересекающийся полуинтервал (разряд) Δ0,...,Δl следующим образом. Действительная ось ℝ1=(−∞,∞)   разделяется точками α0,...,αl+1, образуя таким образом l+1 непересекающийся полуинтервал Δk=[αk,αk+1), k=0,l−−−, при этом −∞=α0<α1<... ...<αl<αl+1=+∞. Обычно выбирают α1≤x(1), αl≤x(n)так, как это сделано при построении гистограммы в .Подсчитывается число nk   элементов выборки, попавших в каждый k -й разряд Δk, k=1,l−1, за исключением Δ0   и Δl. Полагается n0=nl=0

4) Вычисляются гипотетические вероятности pk   попадания СВ X в полуинтервалы Δk, k=0,l. Если у распределения F−(x,θ1,...,θs)   имеется плотность f−(x,θ1,...,θs), то вероятности pk могут быть вычислены следующим образом:

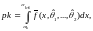
где α0=−∞, αl+1=+∞, или приближенно по формуле

pk≅f−(xk,θˆ1,...,θˆs)(αk+1−αk),  k=1,l−1,

где xk≜(αk+1+αk)/2   — середина разряда Δk.

5) Вычисляется реализация статистики критерия хи-квадрат по формуле

6) Известно, что при соблюдении некоторых естественных условий регулярности и достаточно большом объеме n   выборки Zn   распределение F(z|H0)   статистики Z=ϕ(Zn)   хорошо аппроксимируется распределением χ2(l−s)   с l−s степенями свободы, где s   — количество неизвестных параметров предполагаемого закона распределения F−(x,θ1,...,θs), а l+1   — количество разрядов, вероятность попадания в которые ненулевая. Тогда критическая область 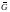принимает вид: =(x1−α(l−s),+∞), где x1−α(l−s)   — квантиль уровня 1−α распределения χ2(l−s), α   — заданный уровень значимости (обычно α=0,05 ).

7) В соответствии с критерием хи-квадрат гипотеза H0   принимается (т.е. реализация выборки zn   согласуется с гипотезой H0 ) на уровне надежности 1−α, если ϕ(zn)∈G=[0,x1−α(l−s)]. Если же ϕ(zn)∈ , то гипотеза H0  отвергается.