4. Выборочные моменты

Пусть имеется выборка Z_n = = col(X₁, ...,Х_п), которая порождена СВ X с функцией распреде­ления F_Х (x).

Определение 4.1. Для выборки Z_n объема п выборочными начальными и центральными моментами порядка r СВ X называются следующие СВ:

Определение 4.2. Выборочным средним и выборочной дис­персией СВ X называются соответственно

Пусть существуют исследуемые моменты ν_г, μ_Т. Тогда справед­ливы следующие свойства.

Свойства выборочных моментов

1) 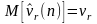для любого 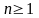и для всех г = 1,2,

2) 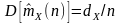, где .

3) .

2. Основные распределения в статистике

1. 1. Распределение хи-квадрат

Определение 2. 1. Пусть U_k, , - набор из n независимых нормально распределенных СВ, ~N(0;1). Тогда СВ

Имеет распределение хи-квадрат с n степенями свободы, что обозначается X_n~χ²(n)

Свойства распределения хи-квадрат χ²(n)

1. СВ X_n имеет следующую плотность распределения:

где - гамма-функция.

2. СВ X_n~χ²(n) имеет моменты:

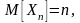
3. Сумма любого числа m независимых СВ X_k, , имеющих распределение хи-квадрат с n_k степенями свободы, имеет распределение хи-квадрат с степенями свободы.

4. Распределение хи-квадрат обладает свойством асимптотиче­ской нормальности:

при

где СВ U имеет распределение N(0;1). Это означает, что при достаточно большом объеме n выборки можно приближенно считать X_n~N(n; 2n). Фактически эта аппроксимация имеет место уже при n > 30.

2.2. Распределение Стьюдента

Определение 2.2. Пусть U и 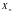— независимые СВ, U ~N(0; 1), ~ χ²(n) . Тогда СВ имеет распреде­ление Стьюдента с n степенями свободы, что обозначают как ~S(n).

Свойства распределения Стьюдента S(n)

1) СВ имеет плотность распределения

2) СВ имеет МО, равное М[Т_n] = 0 для всех n 2, и дисперсию D[ ] = n/(n - 2) при n > 2. При n = 2 дисперсия .

3) Можно показать, что при распределение S (n) асимптотически нормально, т. е. , где СВ U имеет распределение N(0; 1). При n 30 распределение Стьюдента S (n) практически не отличается от N(0; 1).

Точечные оценки.

Параметром распределения СВ X называется любая числовая характеристика этой СВ (мате­матическое ожидание, дисперсия и т.п.) или любая константа, явно входящая в выражение для функции распределения.

В общем случае будем предполагать, что параметр распределе­ния θ может быть векторным, т. е.

В случае параметрической статистической модели ( ) таким параметром распределения может служить неизвестный вектор , характеризующий распределение .

Пусть имеется выборка Z_n = со1(X₁, ... ,Х_п) с реализацией z_n = col(x₁, ...,х_п).

Точечной (выборочной) оценкой неизвест­ного параметра распределения называется произвольная статистика (Z_n), построенная по выборке Z_n и принимающая зна­чения в множестве .

Реализацию (z_n) оценки (Z_n) принимают, как правило, за приближенное значение неизвестного параметра θ.

Несмещенность. Состоятельность

Оценка (Z_n) параметра θ называется несмещенной, если ее МО равно θ, т.е. для любого

Оценка (Z_n) параметра θ называет­ся состоятельной, если она сходится по вероятности к θ, т.е. Р при со для любого .

Оценка (Z_n) параметра θ называется сильно состоятельной, если она сходится почти наверное к θ, т.е. при для любого .

Очевидно, что если оценка сильно состоятельная, то она является также состоятельной.

_{Несмещенная оценка} *(Z_n) скалярного параметра θ называется эффективной, если

Функцией правдоподобия для неизвестного параметра θ∈Θ⊂ℝs   называется: в случае непрерывной наблюдаемой СВ X   — плотность распределения

L(zn,θ1,...,θs)≜fZn(zn,θ1,...,θs)=∏ fX(xk,θ1,...,θs),

где fX(x,θ1,...,θs)   — плотность распределения СВ X, а в случае дискретной наблюдаемой СВ X  — произведение вероятностей

L(zn,θ1,...,θs)≜∏PX(xk,θ1,...,θs),

где PX(xk,θ1,...,θn)   — вероятность события {X=xk}.

Оценкой максимального правдоподобия (МП-оценкой) параметра θ∈Θ  называется статистика θˆ(Zn), максимизирующая для каждой реализации zn функцию правдоподобия, т.е.

θˆ(zn)=argmaxθ∈ΘL(zn,θ).

Способ построения МП-оценки называется методом максимального правдоподобия .

Поскольку функция правдоподобия L(zn,θ)   и её логарифм lnL(zn,θ)   достигают максимума при одних и тех же значениях θ, то часто вместо L(zn,θ)   рассматривают логарифмическую функцию правдоподобия lnL(zn,θ).

В случае дифференцируемости функции lnL(zn,θ)   по θ   МП-оценку можно найти, решая относительно θ1,...,θs   систему уравнений правдоподобия

∂lnL(zn,θ1,...,θs)/∂θ1=0,...,∂lnL(zn,θ1,...,θs)/∂θs=0.