1) п.8. Свойства сложения векторов.
1. Сложение векторов
подчиняется закону ассоциативности,
т.е. ![]() верно
равенство:
верно
равенство:
![]() (1)
(1)
Доказательство.
Воспользуемся правилом треугольника сложения
векторов. Пусть ![]() ,
, ![]() .
Тогда
.
Тогда ![]() .
Отложим вектор
.
Отложим вектор ![]() от
точки С и обозначим его конец буквой D,
так что
от
точки С и обозначим его конец буквой D,
так что ![]() .
.
Тогда
по правилу треугольника ![]() .
С другой стороны, отложим вектор
.
С другой стороны, отложим вектор ![]() и
и ![]() ,
ч.т.д. См. также рис. 9.
,
ч.т.д. См. также рис. 9.
А ![]() В
В
![]()


D С
рис. 9.
2. Существует нулевой элемент относительно сложения векторов, т.е. нулевой вектор:
![]() верны
равенства
верны
равенства ![]() .
.
3.
Для любого вектора ![]() существует
противоположный ему вектор
существует
противоположный ему вектор ![]() ,
такой, что
.
,
такой, что
.
4. Сложение векторов
подчиняется закону коммутативности,
т.е. ![]() верно
равенство:
верно
равенство:
![]() .
.
Последнее свойство сразу же следует из правила параллелограмма сложения векторов.
Таким
образом, мы видим, что множество всех
векторов ![]() относительно операции сложения
является абелевой группой, очевидно,
бесконечной.
относительно операции сложения
является абелевой группой, очевидно,
бесконечной.
Скаляры можно складывать, умножать и делить так же, как обычные числа.
Поскольку
вектор характеризуется не только
числовым значение, но и направлением,
сложение векторов не подчиняется
правилам сложения чисел. Например, пусть
длины векторов a =
3 м, b =
4 м, тогда a + b =
3 м + 4 м = 7 м. Но длина вектора ![]() не
будет равна 7 м (рис. 1).
не
будет равна 7 м (рис. 1).
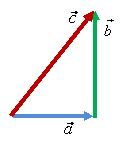
Рис. 1.
Для того, чтобы построить вектор (рис. 2), применяются специальные правила сложения векторов.
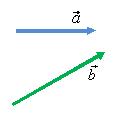
Рис. 2.
А
длину вектора суммы
определяют
по теореме косинусов ![]() ,
где
,
где ![]() –
угол между векторами
–
угол между векторами ![]() и
и ![]() .
.
Правило треугольника
В зарубежной литературе этот метод называют «хвост к голове».
Для
того чтобы сложить два вектора
и
(рис.
3, а) нужно переместить вектор
параллельно
самому себе так, чтобы его начало
совпадало с концом вектора
(рис.
3, б). Тогда их суммой будет вектор ![]() ,
начало которого совпадает с началом
вектора
,
а конец — с концом вектора
(рис.
3, в).
,
начало которого совпадает с началом
вектора
,
а конец — с концом вектора
(рис.
3, в).
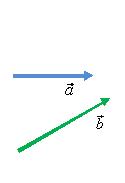
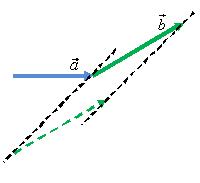
а б в
Рис. 3.
Результат
не поменяется, если перемещать вместо
вектора
вектор
(рис.
4), т.е. ![]() (свойство
коммутативности векторов).
(свойство
коммутативности векторов).
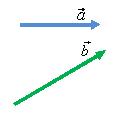


а б в
Рис. 4.
"Правило треугольников" Пример 1
Увеличить Flash
"Правило треугольников" Пример 2
Увеличить Flash
Рис. 5.
При
помощи правила треугольника можно
сложить два параллельных вектора
и
(рис.
6, а) и
и ![]() (рис.
7, а). Суммы этих векторов
и
(рис.
7, а). Суммы этих векторов
и ![]() изображены
на рис. 6, б и 7, б. Причем, модули
векторов
изображены
на рис. 6, б и 7, б. Причем, модули
векторов ![]() и
и ![]() .
.


а б
Рис. 6.
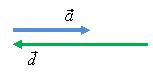

а б
Рис. 7.
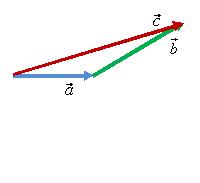
Правило
треугольника можно применять при
сложении трех и более векторов.
Например, ![]() (рис.
8).
(рис.
8).

Рис. 8.
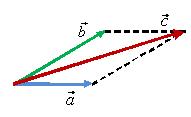
Правило параллелограмма
Для
того чтобы сложить два вектора
и
(рис.
9, а) нужно переместить их параллельно
самим себе так, чтобы начала
векторов
и
находились
в одной точке (рис. 9, б). Затем построить
параллелограмм, сторонами которого
будут эти вектора (рис. 9, в). Тогда
суммой ![]() будет
вектор
,
начало которого совпадает с общим
началом векторов, а конец — с противоположной
вершиной параллелограмма (рис. 9, г).
будет
вектор
,
начало которого совпадает с общим
началом векторов, а конец — с противоположной
вершиной параллелограмма (рис. 9, г).


а б

в г
Рис. 9.
"Правило параллепипеда"
Увеличить Flash
Рис. 10.
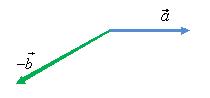
Вычитание векторов
Для
того чтобы найти разность двух
векторов
и
(рис.
11) нужно найти вектор ![]() (см. Умножение
вектора на скаляр)
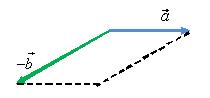
по правилу треугольника (рис. 12) или по
правилу параллелограмма (рис. 13).
(см. Умножение
вектора на скаляр)
по правилу треугольника (рис. 12) или по
правилу параллелограмма (рис. 13).
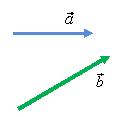
Рис. 11

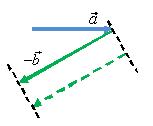
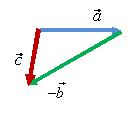
а б в
Рис. 12.
а б

б в
2) п.9. Умножение вектора на число.
Определение.
Произведением вектора
на
действительное число ![]() называется
вектор
,
удовлетворяющий следующим двум условиям:
называется
вектор
,
удовлетворяющий следующим двум условиям:
1) ![]() ;
;
2) ![]() ,
если
,
если ![]() и
и ![]() ,
если
,
если ![]() ;
;
и
обозначается ![]() .
.
Теорема. (Свойства умножения вектора на число.)
1. Свойство ассоциативности: ![]() верно
верно
равенство ![]() .
.
2. Свойство дистрибутивности умножения относительно
сложения чисел: верно равенство
![]() .
.
3. Свойство дистрибутивности умножения относительно
сложения векторов: ![]() верно
равенство
верно
равенство
![]() .
.
4.
верно равенство ![]() .
.
Доказательство. Свойство 4 вытекает из определения умножения вектора на число. Докажем свойство 1.
Умножение
вектора ![]() на
число
можно
интерпретировать как
гомотетию
на
число
можно
интерпретировать как
гомотетию ![]() какой-нибудь плоскости Р,
в которой лежит данный вектор, с центром
гомотетии в начале вектора и коэффициентом
.
какой-нибудь плоскости Р,
в которой лежит данный вектор, с центром
гомотетии в начале вектора и коэффициентом
.
Такая
гомотетия плоскости Р
оставляет точку А на месте, ![]() ,
а конец вектора – точку В переводит
(отображает) в точку С,
,
а конец вектора – точку В переводит
(отображает) в точку С, ![]() ,
причем
,
причем ![]()
и точка С лежит на луче АВ, если и на
противоположном луче, если . См. рис. 10 и 11.
А В С
![]()
![]()
![]()
рис. 10.
С А В
![]()
рис.11.
Теперь свойство 1
следует из того что композиция гомотетий
(т.е. последовательное их выполнение)
есть гомотетия, причем ![]() и
и ![]() верно
равенство:
верно
равенство: ![]() .
.
Пусть ![]() .
.
D А В С
![]()
![]()
![]()
![]() |
|
![]()
![]()
рис. 12.
Тогда ![]() ,
, ![]() и
и ![]() ,
т.е.
,
т.е. ![]() .
.
Таким
образом, ![]() и
,
и
,
следовательно, , ч.т.д.
Доказательство свойства 2
оставляем читателю в качестве
самостоятельного упражнения. Заметим,
что если оба числа
и ![]() имеют
одинаковый знак, то свойство 2
очевидно. Осталось рассмотреть случай
разных знаков чисел
и
.
имеют
одинаковый знак, то свойство 2
очевидно. Осталось рассмотреть случай
разных знаков чисел
и
.
И, наконец, свойство 3 очевидно из следующего
рисунка, построенного для случая :
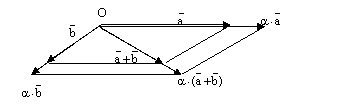
рис. 13.
Заметим, что такая картинка возникает, если мы применим к плоскости, в которой лежат оба вектора, отложенные от одной точки О, преобразование гомотетии с центром гомотетии в точке О икоэффициентом .
Теорема доказана.
Теорема. Множество всех векторов как направленных отрезков впространстве точек S является векторным пространством над полем действительных чисел.
Доказательство следует из свойств сложения векторов и их умножения на действительные числа.
Определение. Векторное пространство над полем действительных чиселназывается вещественным векторным пространством.
Пусть
L произвольная прямая в пространстве S.
Тогда ясно, что ![]() ,
т.е. множество векторов коллинеарных прямой L
является подмножеством всех векторов
.
,
т.е. множество векторов коллинеарных прямой L
является подмножеством всех векторов
.
Далее, сумма любых двух векторов коллинеарных прямой L также является вектором коллинеарным прямой L:
![]() .
В этом случае говорят, что
множество векторов
.
В этом случае говорят, что
множество векторов ![]() замкнуто
относительно сложения векторов.
Аналогично,
замкнуто
относительно сложения векторов.
Аналогично, ![]() ,
т.е. множество
замкнуто
относительнооперации умножения
вектора на действительное число. Отсюда
сразу же следует, что для векторов из
множества
справедливы
все свойствасложения и
умножения на действительные числа, т.е.
справедливы все аксиомы
вещественного векторного пространства.
,
т.е. множество
замкнуто
относительнооперации умножения
вектора на действительное число. Отсюда
сразу же следует, что для векторов из
множества
справедливы
все свойствасложения и
умножения на действительные числа, т.е.
справедливы все аксиомы
вещественного векторного пространства.
Таким образом, множество также является вещественным векторным пространством.
Говорят, что векторное пространство является векторным подпространством векторного пространства .
Аналогично
и для множества ![]() всех векторов лежащих
на некоторойплоскости Р
или на параллельной ей плоскости.
Множества
также
является векторным пространством и
векторным подпространствомвекторного пространства
.
всех векторов лежащих
на некоторойплоскости Р
или на параллельной ей плоскости.
Множества
также
является векторным пространством и
векторным подпространствомвекторного пространства
.
Если
прямая L лежит в плоскости Р
или параллельна ей, то ![]() и
–
подпространство векторного пространства
и
одновременно векторного пространства
.
и
–
подпространство векторного пространства
и
одновременно векторного пространства
.
Векторное пространство мы будем называть пространствомвекторов на прямой L, а –пространством векторов на плоскости Р.
3) Признак коллинеарности векторов.
Для
коллинеарности вектора ![]() ненулевому
вектору
ненулевому
вектору ![]() необходимо
и достаточно, чтобы существовало такое
число λ, что
необходимо
и достаточно, чтобы существовало такое
число λ, что ![]()
Эта теорема доказывается аналогично, как в планиметрии.
§ 6. Коллинеарные векторы.
Два ненулевых вектора, направления которых совпадают или противоположны, называются коллинеарными.
Так, например, на рис. 20 векторы BC> и AD> коллинеарны, а векторы AB> и AC> неколлинеарны.
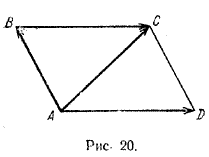
Если векторы а и b коллинеарны, то говорят также, что вектор а коллинеарен векторуb, а вектор b коллинеарен вектору а.
Нулевой вектор считается коллинеарным любому вектору.
Теорема (признак коллинеарности). Для того чтобы вектор а был коллинеарен ненулевому вектору b, необходимо и достаточно, чтобы существовало число k, удовлетворяющее условию
a = kb. (1)
Достаточность. Если при некотором k равенство (1) выполняется, то векторы b и аколлинеарны по определению умножения вектора на число и определению коллинеарных векторов.
Необходимость. Пусть
вектор а коллинеарен
ненулевому вектору b.
Возможны следующие три случая:
а ![]() b, а
b, а ![]() b, а = 0.
b, а = 0.
Если а
b,
то a = ![]() • b,
т. е. равенство (1) выполняется при k =
• b,
т. е. равенство (1) выполняется при k =
Если а b , то a = — • b, т. е. равенство (1) выполняется при k = —
Если а = 0, то а = 0 • b , т. е. равенство (1) выполняется при k= 0.
Задача. Доказать, что векторы AВ> + СВ> + 2 ВА> и 1/3 AС> коллинеарны.
Используя свойства операций над векторами, получим
AВ> + СВ> + 2 ВА> = (AВ> + ВА>) + (СВ> + ВА>) = 0 + ВА> = ВА> = — АС>.
Таким образом,
AВ> + СВ> + 2 ВА> = —3 (1/3 AС>) .
По признаку коллинеарности векторов данные в условии векторы коллинеарны.
4)Вычитание векторов
Чтобы из вектора а вычесть вектор b надо к вектору а прибавить вектор, противоположный вектору b. Полученный в результате этой операции вектор с и будет являться разностью векторов а и b. Таким образом,
с = а − b = а + (− b).
5) Векторы называются компланарными, если имеются равные им вектора, параллельные одной плоскости.
Любые два вектора компланарны. Любые три вектора, среди которых есть два коллинеарных, компланарны.
|
Рисунок 9.2.1 |
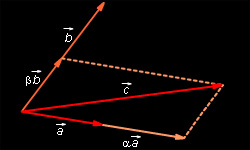
На
рисунке 9.2.1 векторы ![]()
![]() и
и ![]() компланарны,
так как, если отложить от точки C вектор
компланарны,
так как, если отложить от точки C вектор ![]() то
все три вектора
и
то
все три вектора
и ![]() окажутся
лежащими в одной плоскости. Векторы
окажутся
лежащими в одной плоскости. Векторы ![]()
![]() и
не
компланарны, так как вектор
не
лежит в плоскости ACD.
и
не
компланарны, так как вектор
не
лежит в плоскости ACD.
Три вектора называются некомпланарными, если концы равных им векторов, отложенных от одной точки, не лежат в одной плоскости с их общим началом
Теорема о разложении по базису в пространстве.
Любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффициенты разложения определяются единственным образом.
Эта теорема доказывается аналогично теореме 9.4, и поэтому мы не будем на ней подробно останавливаться.
|
Рисунок 9.2.2 |
Отложим
от произвольной точки векторы
и ![]() Спроектируем
конец вектора
Спроектируем
конец вектора ![]() на
прямые, задаваемые векторами
и
на
прямые, задаваемые векторами
и ![]() в
направлении, параллельном другому
вектору (рис. 9.2.2). Обозначим вектора
с началами в точке O и
с концами в полученных точках
соответственно
в
направлении, параллельном другому
вектору (рис. 9.2.2). Обозначим вектора
с началами в точке O и
с концами в полученных точках
соответственно ![]() и
и ![]() Так
как эти вектора лежат на тех же прямых,
что и
,
и
то
по теореме 9.3 существуют
такие числа α и β, что
Так
как эти вектора лежат на тех же прямых,
что и
,
и
то
по теореме 9.3 существуют
такие числа α и β, что ![]()
![]() При
этом по правилу
параллелограмма
При
этом по правилу
параллелограмма ![]() Значит,
Значит, ![]()
Докажем
теперь, что такая пара чисел единственна.
Предположим, что нашлось два разложения
вектора
по
векторам
и
то
есть нашлись две пары чисел ![]()
![]() и
и ![]()
![]() таких,
что
таких,
что ![]()
![]() и
справедливы разложения:
и
справедливы разложения: ![]() и
и ![]() Вычитая
из первого равенства второе,
получаем
Вычитая
из первого равенства второе,
получаем ![]() Отсюда,
ввиду того что
Отсюда,
ввиду того что ![]() следует,
что
следует,
что 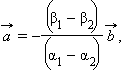 то
есть
то
есть ![]() что
по условию не так. Полученное противоречие
означает, что неравенство
невозможно,
а значит
что
по условию не так. Полученное противоречие
означает, что неравенство
невозможно,
а значит ![]() Аналогично
доказывается, что
Аналогично
доказывается, что ![]() Теорема
доказана.
Теорема
доказана.
Координа́ты ве́ктора ― коэффициенты единственно возможной линейной комбинации базисных векторов в выбранной системе координат, равной данному вектору.
6 )не нашел(