1. Числовые характеристики 2-х мерной св, корреляционный момент, коэффициент корреляции.

Математическое ожидание

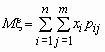
Пусть (x , h ) - двумерная случайная величина, тогда M(x , h )=(M(x ), M(h )), т.е. математическое ожидание случайного вектора - это вектор из математических ожиданий компонент вектора. то математические ожидания компонент вычисляются по формулам: 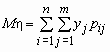Эти формулы можно записать в сокращенном виде.

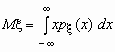
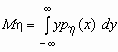
Если (x , h ) - двумерная случайная величина, то

Dx = M(x - Mx )2 = Mx 2 - M(x )2, Dh = M(h - Mh )2 = Mh 2 - M(h )2.

Выборочный корреляционный момент величин X и Y

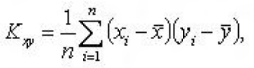
- выборочные средние величин X и Y соответственно.

Выборочный коэффициент корреляции

где - выборочные дисперсии величин X и Y.

Равномерное распределение вероятностей непрерывных СВ.

Опр.: Говорят, что НСВ Х имеет равномерное распределение на [a; b], если f(x) определяется формулой:

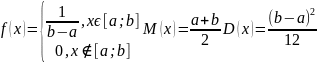График имеет вид:

f(x)

M(х) t

a e Критерий согласия Колмогорова или Критерий согласия Колмогорова-Смирнова — статистический критерий, использующийся для определения того, подчиняются ли два эмпирических распределения одному закону, либо того, подчиняется ли полученное распределение предполагаемой модели.

Билет №8 1. Математическое ожидание СВ и его свойства Определение. Математическое ожидание дискретной случайной величины называется сумма произведений всех возможных ее значений на их вероятности.M(X)=x₁*p₁+x₂*p₂+…+x_np_n=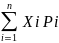

Для непрерыных СВ математическое ожидание определяется по формуле:

M(X)=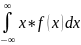

Математическое ожидание есть величина не случайная, тоесть какое-то постоянное число, имеет следующий вероятностный смысл.

1)M(C)=C, где С=const

2)M(Cx)=C∙M(x) док-во аналогично

3)M(x∙y)=M(x)∙M(y), где x и y – независимые СВ

Док-во:

x	x1	x2		y	y1	y­2
p	p1	p2		q	q1	q2

XY	X1Y1	X1Y2	X­2Y1	X2Y2
P	p1q1	p1q2	p2q1	p2q2

M(xy)=x₁y₁∙p₁q₁+ x₁y₂∙p₁q₂+ x₂y₁∙p₂q₁+ x₂y₂∙p₂q₂=(x₁p₁+x₂p₂)(y₁q₁+y₂q₂)=M(x)∙M(y)

Следствие: M(x∙y∙z)=M(x)M(y)M(z), т.к. M((x∙y)∙z)

4)M(x+y)=M(x)+M(y) 2. Закон больших чисел. Теорема Чебышева В теореме Чебышева утверждается, что если рассматривается достаточно большое число независимых случайных величин, то почти достоверным можно считать событие, состоящее в том, что отклонение среднего арифметического случайных величин от среднего арифметического их математических ожиданий будет по абсолютной величине сколь угодно малым. Если X_lt X_it ...,Х_n, -попарно независимые случайные величины, причем диспер­сии их равномерно ограничены (не превышают постоян­ного числа С), то, как бы мало ни было положительное число , вероятность неравенства

Для любой СВ х и любого ξ>0 справедливо неравенство Чебышева :

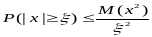3. Статическое распределение выборки. Эмпирическая функция распределения. Эмпирической функцией распределения (функцией рас­пределения выборки) называют функцию /F*(х), опреде­ляющую для каждого значения х относительную частоту события X < х.Итак, по определению,

F*(х) = n_x/n_,

где п_х — число вариант, меньших x; п — объем выборки.

Статистическим распределением выборки называют пе­речень вариант и соответствующих им частот или относи­тельных частот. Статистическое распределение можно за­дать также в виде последовательности интервалов и соответ­ствующих им частот (в качестве частоты, соответствующей интервалу, принимают сумму частот, попавших в этот интервал).

Билет № 9.