
- •Интервальный вариационный ряд и его гистограмма. Выборочная функция плотности. Выборочное среднее и его свойства. Выборочная дисперсия, выборочное среднеквадратическое отклонение и их свойства.
- •Дисперсия нсв и ее свойства. Среднеквадратическое отклонение. Нормированная (стандартная) нсв.
- •Функция распределения нсв и ее свойства. Связь функции распределения с функцией плотности.
- •Математическое ожидание, дисперсия и среднеквадратическое отклонение нсв с равномерным распределением на отрезке .
- •Дисперсия дсв. Выражение дисперсии через математическое ожидание. Отклонение дсв. Среднеквадратическое отклонение.
- •Математическое ожидание дсв и его свойства:
- •Формулы Байеса.
Билет 1.
Размещение и перестановки. Число размещений и перестановок.
а)Пусть
им. Мн-во из n-эл-ов.
Размещением из n-эл-ов
по k
эл-ов назыв. люб.комбинацию k
эл-ов исход. мн-ва отлич.о т др. либо
эл-тами либо их пороядком. Число размещений
из n-эл-ов
по k-эл-ов
обознач. ![]() (
A
из n
по k).
Для подсчета A
из n
по k,
будем подсчитвыать кол-во размещений
из n
эл-ов по одному 1,2,3,… очевидно
(
A
из n
по k).
Для подсчета A
из n
по k,
будем подсчитвыать кол-во размещений
из n
эл-ов по одному 1,2,3,… очевидно ![]() .
Для подсчета
.
Для подсчета ![]() будем строить пары присоединяя к первому
выбронному эл-нту люб. из оставшихся.
Тогда с первым эл-ом на первом месте
можно получить (n-1),столько
же пар можно получить скажем первые
эл-ты и тогда
будем строить пары присоединяя к первому
выбронному эл-нту люб. из оставшихся.
Тогда с первым эл-ом на первом месте
можно получить (n-1),столько
же пар можно получить скажем первые
эл-ты и тогда ![]() .
Для подсчета
.
Для подсчета ![]() будем образовывать тройки из каждой
ранее построенной пары. С каждой пары
можно образовать присоединения один
состав. эл-ов.
будем образовывать тройки из каждой
ранее построенной пары. С каждой пары
можно образовать присоединения один
состав. эл-ов. ![]() (число пар =n(n-1)
слагаемых) тогда продолжая аналогично,
получим
(число пар =n(n-1)
слагаемых) тогда продолжая аналогично,
получим ![]() .
.
![]() Правую часть получ.формулу умножив и
разделив на все послед. убыв. Множители
до ед.
Правую часть получ.формулу умножив и
разделив на все послед. убыв. Множители
до ед. ![]() .
.
![]()
б)
Пусть им.мн-во содерж. n
эл-ов.Перестановкой из n
эл-ов назыв. люб.комбинацию всех этих
эл-ов отлич. от других только порядком
расположений. Число перестановок из n
эл-ов ![]() очевидно
очевидно
![]() Т.О.
Т.О. ![]() .
.
![]()
Билет 2.
Формула полной вероятности.
Пусть
случ. событие B,происходит
вместе с одним из полной системой
несовмест. событий ![]() т.е.
т.е.
![]() Очевидно,
что события, записаные в качестве
слагаемых несовместны. Поэтому по фор-ле
вероятности суммы несовмест.событий.
Очевидно,
что события, записаные в качестве
слагаемых несовместны. Поэтому по фор-ле
вероятности суммы несовмест.событий.
![]() по
фор-ле вероятности произвед.2-ух событий
получим,
по
фор-ле вероятности произвед.2-ух событий
получим, ![]()
![]()
Билет 3.
Сочетание без повторений. Число сочетаний.
Пусть
им. мн-во из n
элементов сочетание из n
эл-ов по k
эл-ов назыв. люб. комбинацию k
эл-ов отлич. от других хотя бы одним
эл-ом.Число сочетаний ![]() .
Для подсчета числа
.
Для подсчета числа ![]() будем строить размещения из n
эл-ов по k
след. образом.Сначала получ. все возможные
сочетания будем получ. размещения будем
получ.размещение эл-ов.каждое сочет.дает
n
из k
размещений.Тогда число размещений
будем строить размещения из n
эл-ов по k
след. образом.Сначала получ. все возможные
сочетания будем получ. размещения будем
получ.размещение эл-ов.каждое сочет.дает
n
из k
размещений.Тогда число размещений ![]() .
.
![]() .
Т.О.
.
Т.О. ![]()
Билет 4.
Свойства
числа сочетаний ![]() ,
,![]() .
.
1)Запишем
фор-лу число сочетаний из n
по k.
![]() и вычислим
и вычислим ![]()
2)Вычислим
число соч. из n
по k
+ соч. из n
по k+1

Билет 5.
Треугольник Паскаля. Формула бинома Ньютона.
Составим
табл. чисел сочетаний
для n=0,1,2,…
и k=0,1,2,…,n.
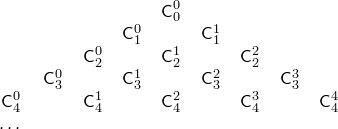
Очевидно,
![]() .Т.О.
боковые стороны этого треугольника
заполнены ед. по 2-ому св-ву, все ост.
числа эти треугольные таблицы равные
сумме двух чисел расположеных над ними.
Эту табл.можно переписать ввиде
.Т.О.
боковые стороны этого треугольника
заполнены ед. по 2-ому св-ву, все ост.
числа эти треугольные таблицы равные
сумме двух чисел расположеных над ними.
Эту табл.можно переписать ввиде
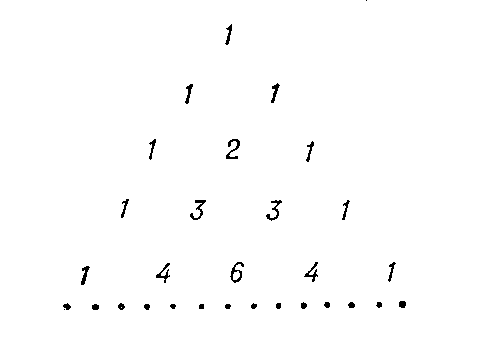
Формула бинома Ньютона. В высшем степени двучлена.
Составить
пирамиду раскрыв скобки по формуле
(a+b)^0=1,
(a+b)^1=a+b,
(a+b)^2=a^2+2ab+b^2
и т.д. до 5-ой степени. Т.О. выполнилась
закономерность:любая степень двучлена
– это сумма число которое служит для
числа из треугольника Паскал, т.е. числа
сочетания. Каждое слагаемое содержит
произведение членов двучлена. Степени
первого члена начинается и так же со
степени дву члена, на ед. убыв. до 0.Степени
второго члена начин. с 0 возр. на ед. до
степени двучлена. Поэтому формула бинома
Ньютона им. вид.![]() .
В более краткой записи
.
В более краткой записи ![]()
Билет 6.
Случайное событие .Сумма и произведение событий. Противоположное событие. Достоверное и невозможное события. Несовместные события.Полная группа событий.
Событие
назыв.случайным, если в одних и тех же
условиях оно может произойти или не
произойти. Создание условий при которых
случайное событие может произойти
назыв.эксперементом. Два случайных
события назыв.несовмест., если они вместе
произойти не могут.Система событий
назыв.полной если в любом эксперименте
одно из них обязательно происходит.Если
в полной системе событии каждая пара
событий не совмест.,такую систему назыв.
полной системой несовмест.событий.Мн-во
событий являющихся полной системы
несовместной событий, назыв. мн-во
исход.эксперимента,если эти события
нельзя выразить через более простые.
Событие A
назыв.благоприятствующим,событию B(AcB)
если при появ.событ.A,событие
B
обязат.происходит. Исход. опытом назыв.
равновозможным,если не одному из них
не по каким причинам нельзя отдать
предпочтения.Классич.определение теории
вероятности:Вероятностью случ.события
назыв.отношения числа исходов
благоприятствующих этому событию чисел
всех возможных исходов.![]() ,где
n-число
всех разновозможных исходов,k-число
исх.благоприят. A.Понятие
вероятности характеризует появ.случ.события
при большом числе экспериментов,она
указывает примерно ту долю исходов
прикоторых наступит случ. событие.
Случайное событие C=A+B
назыв.суммой
случ.событий A
и
B,
если оно происходит,когда происходит
хотябы одно из событий A
или
B.
C=A*B
назыв.произведений
событий A
и
B,если
оно происходило тогда, когда происходят
одновременно оба события Aи
B.
U-событие
назыв.достоверным, если оно происходит
при любом исходе эксперимента.Для
достоверного событие число разновозможных
и благоприятствующих совпадает
k=n,поэтому
P(U)=1.
V-событие
назыв.невозможным,если оно не происходит
не при одном исходе эксперимента, этому
событию благоприятствующих событий
нет,значит вероятность P(V)=0.
,где
n-число
всех разновозможных исходов,k-число
исх.благоприят. A.Понятие
вероятности характеризует появ.случ.события
при большом числе экспериментов,она
указывает примерно ту долю исходов
прикоторых наступит случ. событие.
Случайное событие C=A+B
назыв.суммой
случ.событий A
и
B,
если оно происходит,когда происходит
хотябы одно из событий A
или
B.
C=A*B
назыв.произведений
событий A
и
B,если
оно происходило тогда, когда происходят
одновременно оба события Aи
B.
U-событие
назыв.достоверным, если оно происходит
при любом исходе эксперимента.Для
достоверного событие число разновозможных
и благоприятствующих совпадает
k=n,поэтому
P(U)=1.
V-событие
назыв.невозможным,если оно не происходит
не при одном исходе эксперимента, этому
событию благоприятствующих событий
нет,значит вероятность P(V)=0.
![]() -событие(не
а) назыв.противоположным событие A,если
сумма двух этих событий достоверной,если
A+
=U,A*
=V
.Система
событий
-событие(не
а) назыв.противоположным событие A,если
сумма двух этих событий достоверной,если
A+
=U,A*
=V
.Система
событий ![]() назыв.полным,если
сумма этих событий яв.достоверной.
назыв.полным,если
сумма этих событий яв.достоверной.
![]() .Система
событий
-назыв.полной
системой несовместной событий,если
.Система
событий
-назыв.полной
системой несовместной событий,если ![]()
Билет 7.
Произведение событий.Вероятность произведения двух событий. Независимые события.
Вероятность
события B
при
условии,что событие A
произошло,назыв.условной вероятностью
P(B/A).ТЕОРЕМА.Вероятность
произведения двух событий равна
произведению вероятности одного из них
на вероятность второго при условии что
второе произошло.![]() Док-во:Пусть
в эксперименте равновозможным
n-исходов.Пусть
событию A,
благоприятствует k,событию
AB
благоприят.
L.Тогда
вероятность
Док-во:Пусть
в эксперименте равновозможным
n-исходов.Пусть
событию A,
благоприятствует k,событию
AB
благоприят.
L.Тогда
вероятность ![]() .Пусть
событие A
произошло,это
могло случиться с k-исходными.Вместе
с событием A,событие
Bпроисходит
с l
исходов,тогда
вероятность,что P(B/A)=l/k.Разделим
числитель и знам.полученной дроби на
n.
.Пусть
событие A
произошло,это
могло случиться с k-исходными.Вместе
с событием A,событие
Bпроисходит
с l
исходов,тогда
вероятность,что P(B/A)=l/k.Разделим
числитель и знам.полученной дроби на
n.![]() .Избавились
от знам.получ.
.Избавились
от знам.получ.![]() .
.
Два
события назыв.независимыми,если
вероятность их произведения равна
произведению их вероятности.![]()
C=A*B назыв.произведение событий A и B,если оно проиходило тогда, когда происходят одновременно оба события A и B.
Билет 8.
Сумма событий.Вероятность суммы двух событий.Противоположное событие и его вероятность.
Случайное
событие C=A+B
назыв.суммой
случ.событий A
и
B,
если оно происходит,когда происходит
хотябы одно из событий A
или
B.Вероятность
суммы 2-ух событий равна сумме вероятности
этих событий без вероятности этих
событий без вероятности их произведений.
![]() Док-во:Пусть
в эксперименте n-разновоз.исходами
событию A
благоприят.k,событию
B
l-исходов,событию
AB
m
–исходов.По формуле числа элементов в
объединение 2-ух мн-в событию A+B
благоприятствует k+l+m,тогда
Док-во:Пусть
в эксперименте n-разновоз.исходами
событию A
благоприят.k,событию
B
l-исходов,событию
AB
m
–исходов.По формуле числа элементов в
объединение 2-ух мн-в событию A+B
благоприятствует k+l+m,тогда![]() .
.![]() -событие(не
а) назыв.противоположным событие A,если
сумма двух этих событий достоверной,если
A+
=U,A*
=V
.P(
-событие(не
а) назыв.противоположным событие A,если
сумма двух этих событий достоверной,если
A+
=U,A*
=V
.P(![]()
Билет 9.
Схема Бернулли.Формула Бернулли вероятности k появлений случайного события в n независимых испытаниях.
Пусть
в эксперименте случ.событие A
происходит с вероятностью P(A)=p
и
не происходит с
вероятностью
.P(![]() .Пусть
испытание повторяется ровно n
раз ирезультат каждого испытания
независ.от результатов пред.испытаний.Треб.найти
вероятность того чтоб в n
испытаниях события A
произойдет
ровно m
раз
.Пусть
испытание повторяется ровно n
раз ирезультат каждого испытания
независ.от результатов пред.испытаний.Треб.найти
вероятность того чтоб в n
испытаниях события A
произойдет
ровно m
раз
![]() .Обозначим
.Обозначим
![]() ,событие
,событие
![]() произошло с испытанием I
и с номером I,
произошло с испытанием I
и с номером I,![]() .тогда
события сост. В том что в n
испытаниях
событие A
произойдет ровно m
раз.Можно представить в виде
.тогда
события сост. В том что в n
испытаниях
событие A
произойдет ровно m
раз.Можно представить в виде ![]() (*).Т.к.появ.
события A
в
каждом испытании независ. от остальных,но
вероятность события(*) равна произведению
вероятности входящих в него
событий.
(*).Т.к.появ.
события A
в
каждом испытании независ. от остальных,но
вероятность события(*) равна произведению
вероятности входящих в него
событий.![]() .Событие
сост. в том,что n
испытаний
A
произойдет
n
раз
представ. Собой сумму событий вида(*),
где
.Событие
сост. в том,что n
испытаний
A
произойдет
n
раз
представ. Собой сумму событий вида(*),
где ![]() -это
различные подмнож-ва номеров испытаний
1,2,…,n.Число
таких подмнож-в равно
-это
различные подмнож-ва номеров испытаний
1,2,…,n.Число
таких подмнож-в равно ![]() для каждого из таких событий вероятности
равна(**).Событие вида(*)-несовместна,поэтому
вероятность их суммы равна просто суммы
вероятности,значит для получения
вероятности
нужно
сложить слагаемые на
для каждого из таких событий вероятности
равна(**).Событие вида(*)-несовместна,поэтому
вероятность их суммы равна просто суммы
вероятности,значит для получения
вероятности
нужно
сложить слагаемые на ![]() равно
значит
равно
значит ![]() .Если
требуется найти вероятность того что
в n
испытаниях
событие A
произойдет число раз n
в
пределах от Aдо
B
то
получ.вероятности
нужно сложить
.Если
требуется найти вероятность того что
в n
испытаниях
событие A
произойдет число раз n
в
пределах от Aдо
B
то
получ.вероятности
нужно сложить ![]() .
.
Билет 10.
Понятие случайной величины.Дискретная случайная величина.Закон распределения ДСВ.Ряд распределения ДСВ.Полигон распределения.
Случайным назыв.величина которая в результате эксперимента может применять одно из некоторого мн-во случ.значений.Случайное событие назыв.дискретной,если между ее возможными значениями существ.др.знач.,которую принять не может.Законом распределения ДСВ назыв.любое соответ.между возможными значениями и их вероятности.Законом распределения в виде таблицы значение и соответ. Им вероятности назыв.рядом распредлений.Табличное задание закона распред.напомин. табл.заданиеf-ии.функцию часто задают графически,аналогично с помощью графика можно изобразить закон распределения, этот граф назыв. мноугольником или полигоном распределения.Для его построения в системе коорд. по соответст.значение случ. величины и их вероятностями строят точки и соединяют их отрезками.
Билет 11 Функция распределения ДСВ ее свойства.
Функция F(x) называется функцией распределения случайной величины х если она определяется выражением F(x)=P(X<x) т.е функция распределения это вероятность того, что значение случайной величины меньше аргумента этой функции.
F(x) это сумма вероятности того что х принимает значение x+i по всем значениям меньше чем х
F(A)=![]()
Свойство функции распределения
Область определения D(F(x))=(-∞;∞)
Множество значений E(F(x))=[0;1] т.к это вероятность
F(x)=0 при x<=
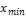
F(x)=1 при x<=

F(x) =c при x
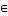 (
( ;
; )
)F(x) неубываю. функция и вероятность того что случ. величина примет от а до b равно b-a
P(a<x<b)=F(b)-F(a)
Функция распределения для двумерной случайной величины F(x,y)=P(X<x,Y<y) изобразим геометрически возможные значения даумернрй случайной величины
y
|
F(x,y)=![]()
Билет
12 Математическое ожидание ДСВ и его
свойства:
![]() .
.
Математическим
ожиданием МХ случайной величины х
называют сумму произведений всех
возможных значений ДСВ на их вероятности
МХ=![]() где
где ![]() =P(X=
)
=P(X=
)
Выясним смысыл математического ожидания. Пусть проводится опыт в котором случайная величина х может принять значение {x1,x2,x3,..,xn} в опыте возможно n равновозможных исходов.
Пусть к1 примет значение х1 исходов, к2 х2 исходов, …, km-xn. k1-k2-…km=n, тогда P1=k1/n, P2=k2/n, Pm=km/n
Вычислим
![]() средняя арифметическая возможное
значение случайной величины по всем
исходам опыта.
=
средняя арифметическая возможное
значение случайной величины по всем
исходам опыта.
=![]() =
=![]() =
x1
=
x1![]() +
x2
+
x2![]() +…+
xm
+…+
xm![]() =x1P(1)+x2P(2)+…xmPm=MX
=x1P(1)+x2P(2)+…xmPm=MX
Т.О МХ это средняя арифметическая всех возможных значений ДСВ по всем исходам эксперимента.
Свойства МХ:
Математическое ожидание постоянной равно МС= С
Док-во: постоянную можно рассматривать как случайную величину принимающую единственное значение С с вероятностью р=1. Тогда МС=С*1=С
Математическое ожидание суммы случайных величин равна сумме их математических ожиданий. M(X+Y)=MX+MY
Док-во:
Пусть возмоное значение случайной
величины Х х1,х2,…,хn
которая она принимает с вероятностью
P1,P2,…Pn
и соответственно для случайной величины
Y
возможны значения y1,y2,…,yn
и q1,q2,…,qn
обозначим Pij=P(X=xi,Y=yj)
тогда ![]() =Pij+Pij+…Pnj=qj(По
формуле полной вероятности)
=Pij+Pij+…Pnj=qj(По
формуле полной вероятности)
Рассмотрим
математ. ожидание М(Х+У)![]() =
=![]() =(С
начала сложим все слагаемые с Xi
а затем все слагаемые Yj)=
=(С
начала сложим все слагаемые с Xi
а затем все слагаемые Yj)=
![]() +
+![]() =
=
(первое
слагаемое перепишем а во втором слагаемом
изменим порядок суммирования – сначала
по индексу i
а потом по индексу j)
=![]() +
+![]() =
(Во внутренних суммах обоих слагаемых
есть общий множитель соответственно
Xi
и Yj
который вынесем за скобки)
=
(Во внутренних суммах обоих слагаемых
есть общий множитель соответственно
Xi
и Yj
который вынесем за скобки)
![]()
Билет
13
Дисперсия ДСВ и ее свойства:
![]() .
.
Для получения представления о разбросе возможных значений ДСВ относительно ее математического ожидания вводят понятие Дисперсии.
Дисперсия
ДСВ называют матем. Ожидание квадрата
ее отклонения DX=M(X-MX)2
. Из определения дисперсии следует
DX=![]() 2Pi
2Pi
Свойства дисперсии:
Дисперсия постоянной равно 0 DC=0
Док=во: По определению Дисперсия Постоянной это математическое ожидание постоянной
DC=M(C-MC)2 M(C-C)2 M0=0
Постоянный множитель можно вынести за знак дисперсии предварительно возведя ее в квадрат
D(CX)=C2 DX
Док-во: по определению D(CX)=M(CX-M(CX))2 =M(CX-CMX)2=M(C(X-MX))2=M(C2(X-MX)2)=C2M(X-MX)2=C2DX
Дисперсия
суммы и разности 2 независимых случ.
величин равна сумме дисперсии этих
величин. D(X![]() Y)=D(X)+D(Y)
Y)=D(X)+D(Y)
Док-во:
по определению D(X
Y)=
M((X
Y)-
M(X
Y))2
(Во внешние скобки перегруппируем 4
слагаем.)=M((X-MX)![]() Y-MY))2
=(возведем в квадрат)=M((X-MX)2
2(X-MX)(Y-MY)+(Y-MY)2)=
Y-MY))2
=(возведем в квадрат)=M((X-MX)2
2(X-MX)(Y-MY)+(Y-MY)2)=
(По
теореме об математических ожиданиях
суммы и разности)=M(X-MX)2![]() M(2(X-MX)(Y-MY))+N(Y-MY)2=(Первые
и последние слагаемые это дисперсии а
во втором слагаемом есть постоянный
множитель и произведения независимых
случайных величин)=DX
2M(X
MX)(Y
MY)+DY(Математическое
ожидание отклонения равна 0)=DX+DY
M(2(X-MX)(Y-MY))+N(Y-MY)2=(Первые
и последние слагаемые это дисперсии а
во втором слагаемом есть постоянный
множитель и произведения независимых
случайных величин)=DX
2M(X
MX)(Y
MY)+DY(Математическое
ожидание отклонения равна 0)=DX+DY
Билет 14 Нормированная (стандартная) ДСВ, ее математическое ожидание, дисперсия и среднеквадратическое отклонение.
Нормированной или стандартной называется случайная величина Z=X-MX/σx
Рассмотрим
Матем.ожид. MZ=M(X-MX/σx)=![]() M(X-MX)=
M(X-MX)=![]() *0=0.
*0=0.
Найдем
дисперсию
DZ=D(X-MX/σx)=![]() D(X-MX)=
(DX+D(MX))=
(DX+0)=
D(X-MX)=
(DX+D(MX))=
(DX+0)=![]()
![]() =1
=1
Т.О. Математическое ожидание нормированной ДСВ равна 0 и дисперсия равна 1
Билет 15. Биномиальное распределение ДСВ, его математическое ожидание, дисперсия и среднеквадратическое отклонение.
Случайная
величина х принимающая щначения 0,1,2,…т,
с вероятностями P(x=m)=![]() pmqn-m
где p>0,q>0,
называется ДСВ с биномиальным
распределением
pmqn-m
где p>0,q>0,
называется ДСВ с биномиальным
распределением
Составим ряд распределения
x |
0 |
1 |
2 |
… |
m |
… |
n |
p |
qn |
npqn-1 |
|
|
pmqn-m |
|
pn |
Запишем функцию распределения
F(X)=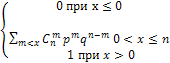
Для
получения математического ожидания и
дисперсии запишем формулу бинома ньютона
(a+b)n=![]() Найдем 1 и 2 производные от обеих частей
равенства 1 по переменной a
Найдем 1 и 2 производные от обеих частей
равенства 1 по переменной a
1а:
n(a+b)n-1=
![]() (2)
(2)
2a:
n(n-1)(a+b)n-1=![]() (3)
(3)
В
равенство 2 положим a=p
,b=q
и учтем , что p+q=1
n=
![]() |*p
обе части равенства умножим на p;
np=
|*p
обе части равенства умножим на p;
np=
![]() выражение с права это математическое
ожидание т.е. MX=np
выражение с права это математическое
ожидание т.е. MX=np
Для получения дисперсии подставим в равенство 3 a=p, b=q, p+q=1
n(n-1)=![]() умножим обе части на p2
умножим обе части на p2
n(n-1)p2=![]() с права раскроем скобки и отдельно
посуммирем слагаемые с множителем m2
и с множителем m
n(n-1)=
с права раскроем скобки и отдельно
посуммирем слагаемые с множителем m2
и с множителем m
n(n-1)=![]() -
-
с
права последняя сумма это математическое
ожидание а 1 это математическое ожидание
квадрата т.е. n(n-1)p2=MX2-MX
или n(n-1)p2=
MX2-np
Отсюда MX2=
n(n-1)p2+np
тогда DX=
MX2-
(MX)2=
n(n-1)p2+np-n2p2=
n2p2-np2+np-
n2p2=np(1-p)=npq
Т.О. DX=npq
тогда среднеквадратическое отклонение
![]() =
=![]()
Билет 16 Геометрическое распределение ДСВ, его математическое ожидание, дисперсия и среднеквадратическое отклонение.
Геометрическое распределение
Определение. Случайная величина х принимающая значение 0,1,2,… n… с вероятностью P(x=m)=pqm где p>0 p+q=1 q>0
Называется ДСВ с геометрическим распределением.
Составим ряд распределения
x |
0 |
1 |
2 |
… |
m |
… |
|
p |
P |
Pq |
pq2 |
|
pqm |
|
|
Значением функции распределения
F(X)=![]()
Полученное
выражение действительно задает функцию
распределения если сумма всех элементов
2 строки ряда распределения равна 1.
Чтобы проверить это заметим что эти
числа представляют собой бесконечную
убывающую геометрическую прогрессию.
Сумма всех членов такой прогрессии с
первым членом равное а и знаменателем
q
вычисляется по формуле![]() =
=![]() (1).
Подставим в эту формулу a=p
(1).
Подставим в эту формулу a=p
![]() =
=![]() =
=![]() =1
=1
Для получения математического ожидания и дисперсии вычислим 1 и 2 производные равенства 1 по переменной q предворительно переписав его
=a(1-q)-1 тогда
1a
= ![]() =
=![]() (2)
(2)
2a=![]() =
=![]() (3)
(3)
Подставим в равенство 2 a=p
![]() =
=![]() |q
умножим обе части на q
|q
умножим обе части на q
![]() =
=![]() Сумма с лева математическое ожидание
MX=
=
Сумма с лева математическое ожидание
MX=
=![]() =
=![]() Т.О. MX=
Т.О. MX=
Для
получения дисперсии подставим a=p
в равенство 3 ![]() =
=![]() |q2множим
обе части на q2
|q2множим
обе части на q2
![]() =
=![]() Слева раскроем скобки и отдельно сложим
слагаемые с m2
и с m.
Слева раскроем скобки и отдельно сложим
слагаемые с m2
и с m.
![]() -
-![]() =
MX2-MX=
отсюда MX2
=
=
MX2-MX=
отсюда MX2
=![]() +
+![]() тогда Дисперсия DX=MX2-
(MX)2=
+
-
тогда Дисперсия DX=MX2-
(MX)2=
+
-![]() ) 2
=
) 2
=![]() +
+![]() -
-
![]() =
=![]()
DX=![]()
![]() =
=![]()
Билет
17 Непрерывная
случайная величина. Геометрическое
определение вероятности. НСВ с равномерным
распределением на промежутке
![]() и ее функция распределения
и ее функция распределения
Понятие НСВ геометрический подход.
Случайная величина называется непрерывной если ее возможное значение занимают целиком некоторый числовой промежуток.
Для определения вероятности попадания НСВ в некоторый числовой промежуток использовать классическое определение нельзя т.к. числа равновозможных и благоприятствующих исходов бесконечно. В этом случае пользуются геометрическим определением вероятности:
Пусть точка бросается на отрезок длины L так что все ее положения в нутрии этого отрезка равновозможные. Вероятность того что точка попадет на внутреннюю часть этого отрезка длинной L называют отношением длин внутреннего и исходного отрезка P(x L)=1/L
Для
двумерной случайной величины z=x*y
каждое значение определяется парой xy
т.е. точками на плоскости пусть точка
бросается внутрь некоторой ![]() так что все ее положение в этой фигуре
равновозможны. Вероятность у того что
точка попадет в некоторую часть
так что все ее положение в этой фигуре
равновозможны. Вероятность у того что
точка попадет в некоторую часть ![]() (малая)
этой фигуры называют отношения площадей
внутренней и внешней фигуры P(x,y)
(малая)
этой фигуры называют отношения площадей
внутренней и внешней фигуры P(x,y)![]() )=
)=![]()
НСВ называется равномерно распределенной на промежутке[a,b] если вероятность попадания ее внутрь части этого промежутка зависит только от длины этой части и не зависит от ее положения внутри этого промежутка.
Функция распределения НСВ называют вероятностью того что случайная величина примет значение меньшее аргумента этой функции. F(x)=P(X<x) составим функцию распределения для НСВ с равномерным распределением на промежутке [a,b].
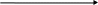 a
x
b
a
x
b
Если
xx<=a
то F(x)=P(X<x)=0
т.к. левее выборочные точки нет ни одного
возможного решения НСВ. Пусть х находится
в промежутке от а<=x<=
b
тогда F(x)=P(X<x)=![]() где х-а длина меньшего отрезка
где х-а длина меньшего отрезка ![]() длина
исходного отрезка тогда все возможные
значения НСВ расположенные левее
выборочной точки поэтому F(x)=1
т.о.
длина
исходного отрезка тогда все возможные
значения НСВ расположенные левее
выборочной точки поэтому F(x)=1
т.о.
F(X)=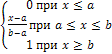
График функции распределения
F(x) 1
|
Билет 18. Функция плотности НСВ и ее свойства. Связь с функцией распределения.
Функцией плотности НСВ . называют производную от ее распределения. F(x)=F’(x)
Эту функцию также называют дифференциальная функция распределения .
Св-ва функции плотности:
1)f(X)>= 0 Т.К. производная неубывающей функции распределения.
2)P(a<=x<=b)=F(b)-F(a)![]() , т.е. вероятность попадания НСВ на
промежуток от [a;b]
равна определенному интегралу от функции
плотности.
, т.е. вероятность попадания НСВ на
промежуток от [a;b]
равна определенному интегралу от функции
плотности.
3)![]() =F(∞)-F(-∞)=1-0=1
т.е. интеграл от функции плотности по
всей числовой оси равен 1, т.е. S
фигуры ограниченной графиком функции
плотности и осью OX
всегда равен 1
=F(∞)-F(-∞)=1-0=1
т.е. интеграл от функции плотности по
всей числовой оси равен 1, т.е. S
фигуры ограниченной графиком функции
плотности и осью OX
всегда равен 1
4)Рассмотрим
![]() =F(x)-F(-∞)=F(x)-0=F(x)
таким образом F(x)=
=F(x)-F(-∞)=F(x)-0=F(x)
таким образом F(x)=
Т.е. функция Распределения это определенный интеграл от функции плотности, поэтому функцию распределения часто называют интегральной функцией распределения, а функцию плотности дифференциальной функцией распределения.
Связь
. F(x)=F’(x)
![]()
Билет 19 Математическое ожидание НСВ и его свойства. Медиана НСВ.
Матем.
ожиданием НСВ
называют MX![]() где f(x)
функция плотности этой функции.
где f(x)
функция плотности этой функции.
Т.к. Матем. Ожидание НСВ получено из математического ожидания ДСВ с помощью предельного перехода то все свойства матем. Ожидания сохраняются. MC=C
M(X![]() Y)=MX+MY,
M(CX)=CMX,
M(XY)=MX*MY
для независимых
Y)=MX+MY,
M(CX)=CMX,
M(XY)=MX*MY
для независимых
Медианой НСВ m называют такое значение случ. величины что вероятность того что случ. величина примет значение меньше медианы равна P(X<m)=1/2
Исходя
из определения медианы фнкция распределения
и функция плотности следует F(m)=1/2
![]()
Если случайная величина определена на всей числовой оси то по определению матем. Ожидание
Билет 20. Нормальное распределение НСВ, математическое ожидание и дисперсия.
1)НСВ
распределена по нормальному закону
если ее функция плотности имеет вид
![]() где а и б параметры нормального
распределения. ПО свойствам функции
плотности ф-я распределения нормальной
НСВ
где а и б параметры нормального
распределения. ПО свойствам функции
плотности ф-я распределения нормальной
НСВ ![]() .
Для выяснения смысла параметров
нормального распределения найдем MX,
DX.
Нормальной НСВ. Для этого воспользумся
двумя известными из мат. Анализа Данными:
если f(x)
нечетно
.
Для выяснения смысла параметров
нормального распределения найдем MX,
DX.
Нормальной НСВ. Для этого воспользумся
двумя известными из мат. Анализа Данными:
если f(x)
нечетно ![]() Интеграл Пуассона
Интеграл Пуассона ![]() Найдем MX=
Найдем MX=

![]() +
+![]()
![]() (первый из интегралов это интеграл
от нечетной функции, а 2-это интеграл
Пуассона) Т.О. MX=а
(первый из интегралов это интеграл
от нечетной функции, а 2-это интеграл
Пуассона) Т.О. MX=а
DX=![]() Можно показать, что дисперсия нормальной
НСВ DX=б^2
таким образом а-мат. Ожидание,
б-среднеквадратическое отклоненеие.
Можно показать, что дисперсия нормальной
НСВ DX=б^2
таким образом а-мат. Ожидание,
б-среднеквадратическое отклоненеие.
Билет 21. Функция плотности нормального распределения, ее свойства и график.
Построим график функции плотности . Для этого рассмотрим ее св-ва:
А)D(f)=(-![]() )
так как это показательная функция.
)
так как это показательная функция.
Б)f(x)>0 по св-ву показательной функции .
В)рассмотрим
![]() т.е. график имеет горизонтальную
асимптоту.
т.е. график имеет горизонтальную
асимптоту.
Г)найти
экстремумы функции f’(x)=![]() при x=a
Левее этой точки производная положительна,
а правее отрицательна, т.е. в этой точке
максимум, его координаты (a;
при x=a
Левее этой точки производная положительна,
а правее отрицательна, т.е. в этой точке
максимум, его координаты (a;![]() )
)
Д) рассмотрим 2 значения аргумента , симметричнее относительно MX . x1=a-Ɣ x2=a+Ɣ Легко убедиться подстановкой этих значений что f(x1)= f(x2) т.е. график функции плотности симметричен относительно прямой x=a
Е)вычислив
2 производную можно убедиться что график
имеет 2 точки перегиба, с абсциссами а=б
и ординатой ![]() по полученным св-ам получим график
по полученным св-ам получим график
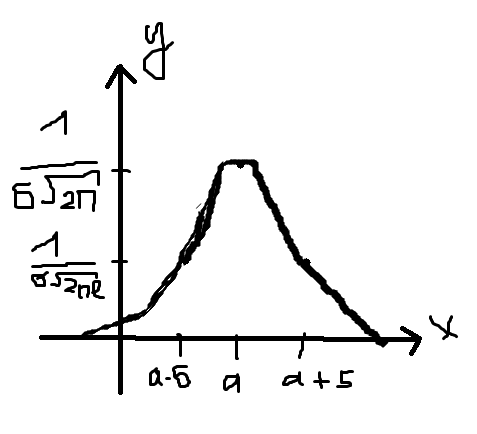
Легко увидеть влияние параметров распределения на график фун-и плотности, при изменении математического ожидания и график смещается горизонтальная . Среднеквадротическое отклонение влият она крутизну. Чем <б тем выше точка максимума и круче график.
Билет 22. Показательное распределение НСВ, его характеристики.
Нсв
называют распределенной по показательному
закону, если ее ф-я плотности имеет вид.
F(x)
![]() где
где ![]() положительное число, параметр
показательного распределения.
положительное число, параметр
показательного распределения.
Для построения графика функции плотности рассмотрим ее св-ва при x>0
1)f(x)>0
так как показательная ф-я 2)рассмотрим
предел ![]() =
=![]() т.е. в точке x=0
ф-я имеет разрыв .
т.е. в точке x=0
ф-я имеет разрыв .
3)рассмотрим
предел ![]() =0 т.е. график имеет горизонтальную
ассимтоту x->∞
ось ox.
=0 т.е. график имеет горизонтальную
ассимтоту x->∞
ось ox.
4)f’(x)=![]()
5)f”(x)=-![]() график имеет выпуклость вниз.
график имеет выпуклость вниз.
Билет 23. Функция плотности показательного распределения, ее свойства и график. Функция распределения и ее график.
Нсв называют распределенной по показательному закону, если ее ф-я плотности имеет вид. F(x) где положительное число, параметр показательного распределения.
Для построения графика функции плотности рассмотрим ее св-ва при x>0
1)f(x)>0
так как показательная ф-я 2)рассмотрим
предел
=![]() т.е. в точке x=0
ф-я имеет разрыв .
т.е. в точке x=0
ф-я имеет разрыв .
3)рассмотрим предел =0 т.е. график имеет горизонтальную ассимтоту x->∞ ось ox.
4)f’(x)=
5)f”(x)=- график имеет выпуклость вниз.
Исходя из полученных св-ств построим график.
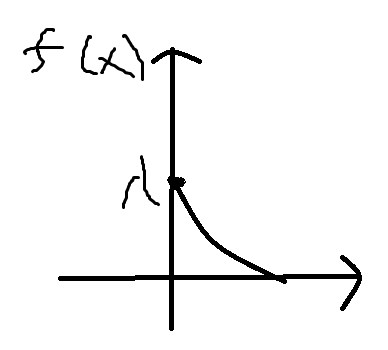
Запишем для НСВ функцию распределения
F(x)=![]() x<=
0 : F(x)=
x<=
0 : F(x)=![]() F(x)=
F(x)=![]() так. Обр. F(x)=
так. Обр. F(x)=![]() График этой функции с учетом известного
графика показательной функции.
График этой функции с учетом известного
графика показательной функции.
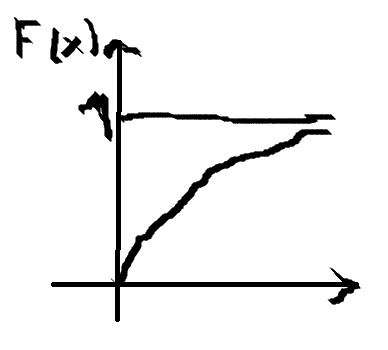
Билет 24. 1. Генеральная и выборочная совокупности. Вариационный ряд, размах выборки, варианта, частота и относительная частота варианты. Дискретный вариационный ряд распределения. Полигон частот и относительных частот. Выборочная функция распределения.
Генеральной совокупность называют набор числовых характеристик всего множества изучаемых объектов. Обычно число N таких объектов очень велико. Выборочночной совокупностью или просто выборкой называют набор числовых характеристик св-ств небольшой части объектов из всего мн-ва. Их кол-во n значительно меньше чем N называют объемом выборки . Обычно при получении выборки все значения ее располагаются в произвольном порядке . Это неудобно для изучения поэтому эту выборку рапнируют (т.е. располагают в порядке возрастания ). Рапнированною выборку называют вариационным рядом . Пусть Xmin и Xmax соответственно минимальное и максимальное значение эл. Выборки называют размахом выборки . В любой выборке могут встречаться одинаковые эл-ты. Поэтому вместо вариационного ряда удобно записать различные эл-ты выборки и соответствующие им кол-во их хождений в вариационный ряд.
x-элементы |
X1 |
X2 |
…. |
Xk |
m- количество |
M1 |
M2 |
…. |
Mk |
В этой таблице Xi варианта , Mi частота. Таблица называется вариационным рядом распределения частот. Очевидно m1+m2…mk=n вместо частот можно рассматривать относительные частоты . (Ṕ- короче это P с хвостиком наверху) Ṕi=mi/n тогда вместо вариационного ряда распределения частот можно составить вариационный ряд распределения относительно частот.
x-элементы |
X1 |
X2 |
…. |
Xk |
Ṕ |
Ṕ1 |
Ṕ2 |
|
Ṕk |
И вариационный ряд распределения частот и ряд относительных частот можно изобразить геометрически. С помощью полигона частот или относительно частот.
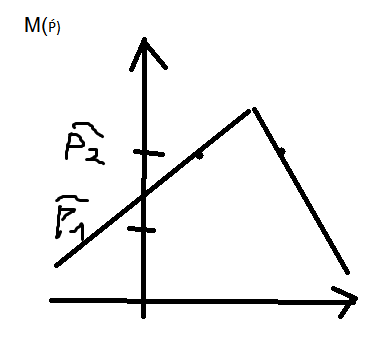
Вариационную фун-ю распределения Ḟ(x ) называют относительной частотой всех вариант выборки меньших аргумента этой фун-и. Ḟ(x)=Ṕ(X<x) в вмде таблицы фун-я распределения имеет вид
X |
(0;x1] |
(x1;x2] |
(x2;x3] |
…. |
(xn;∞) |
F(x) |
0 |
Ṕ1 |
Ṕ1+ Ṕ2 |
…. |
1 |
Т.е. функцию распределения можно записать формулой
Ḟ(x)=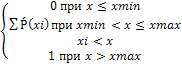
Билет 25
Интервальный вариационный ряд и его гистограмма. Выборочная функция плотности. Выборочное среднее и его свойства. Выборочная дисперсия, выборочное среднеквадратическое отклонение и их свойства.
Обычно при получении выборки все значения ее располагаются в произвольном порядке это неудобно для изучения поэтому эту выборку ранжируют, т.е. располагают в порядке возрастания. Ранжированную выборку называют вариационным рядом.
Если число вариант выборки больше 7-10, то ряды распределения не удобны для изучения, поэтому вместо вариационных рядов составляют интервальные вариационные ряды, разбивая промежуток [xmin,xmax] на 7-10 равных интервалов и суммируя частоты вариант входящих в этот интервал
Гистограмма – ступенчатая фигура, состоящая из прямоугольников, основания которых частичные интервалы, высоты равны отношению частоты к длине частичного интервала.
Выборочной
функцией распределения ![]() (x)
называют относительную частоту всех
вариант выборки меньших аргумента этой
функции.
(x)=
(x)
называют относительную частоту всех
вариант выборки меньших аргумента этой
функции.
(x)=![]() (Х<x)
(Х<x)
В виде таблицы функция распределения имеет вид:
Х |
(0;x1] |
(x1;x2] |
(x2;x3] |
… |
(xn; |
(x) |
0 |
|
|
… |
1 |
Т.е. функцию распределения можно записать формулой:
(x)=
Выборочно средним называют среднеарифметическое всех вариант выборки.
![]() =
= ![]() или
= x1
1+x2
или
= x1
1+x2![]() +…+xk
+…+xk![]()
Выборочная
средняя определяется подобно тому, как
мат. Ожидание для ДСВ, поэтому и свойства
их совпадают, т.е. ![]() =C,
=C,
![]() =
=![]() ,
,
![]() =C
и т.д.
=C
и т.д.
Выборочным отклонением называют разность варианты и выборочного среднего
-Х
Выборочной дисперсией называют выборочное среднее квадрата отклонений,
![]() X=
X=![]()
Свойства выборочной дисперсии такие же как у дисперсии ДСВ, в частности для вычисления выборочной дисперсии
X=![]() -
-
![]()
Выборочным
среднеквадратическим отклонением
называют арифметический квадратный
корень из выборочной диспресии ![]() =
=![]()
Числовые характеристики выборки используют для получения характеристик генеральной совокупности.
Выборочная
дисперсия несколько смещена, относительно
дисперсии генеральной совокупности.
Можно показать, что несмещенная выборочная
дисперсия вычисляется по формуле: ![]() =
= ![]() X
X
Билет 26
Дисперсия нсв и ее свойства. Среднеквадратическое отклонение. Нормированная (стандартная) нсв.
DX=![]()
Свойства дисперсии:
1)DC=0
2)D(X![]()
3)D(CX)=![]() DX
DX
4)DX=M![]() -
-![]()
Среднеквадратическое
отклонение ![]() =
=![]()
Нормированной
или стандартной называется НСВ имеющая
вид: z=![]()
Билет 27
Функция распределения нсв и ее свойства. Связь функции распределения с функцией плотности.
1)Функцией распределения НСВ называют вероятность того что НСВ примет значение меньше аргумента этой функции:
F(x)=P(X<x)
Свойства:
1)Область
определения D(F)=(![]()
Следует из определения.
2) Область значений E(F)=[0;1], т.к. это вероятность.
3)F(x)-
неубывающая и P(a![]()
Доказательство:
Рассмотрим
3 события: А= «Х<a»,
B=
«X<b»,
С=«a![]() »,
события А и С несовместимы и событие
В=А+С, тогда вероятность Р(В)=Р(А+С)=Р(А)+Р(С),
тогда Р(С)=Р(В)-Р(А),тогда
»,
события А и С несовместимы и событие
В=А+С, тогда вероятность Р(В)=Р(А+С)=Р(А)+Р(С),
тогда Р(С)=Р(В)-Р(А),тогда
Р(а![]() Р(X<b)-Р(Х<a)=F(b)-F(a).
Т.к. записанная разность неотрицательна,
то большему значению аргумента
соответствует большее или равное
значение функции, значит она не убывающая.
Р(X<b)-Р(Х<a)=F(b)-F(a).
Т.к. записанная разность неотрицательна,
то большему значению аргумента
соответствует большее или равное
значение функции, значит она не убывающая.
4)F(-![]() ,
F(
,
F(![]()
Доказательство:
Будем
принимать эти значения, F(-![]() =
=![]() ,
F(
=
,
F(
=![]() ,
по свойству 2 функция ограничена, по
свойству 3 она монотонна, из анализа
известно, что для любой монотонной
ограниченной функции, записанные пределы
существуют. Т.к. , F(-
=Р(Х<-
,
то это вероятность невозможного события
и значит она равна 0. Т.к. F(
=Р(Х<
,
это вероятность достоверного события,
то она равна 1.
,
по свойству 2 функция ограничена, по
свойству 3 она монотонна, из анализа
известно, что для любой монотонной
ограниченной функции, записанные пределы
существуют. Т.к. , F(-
=Р(Х<-
,
то это вероятность невозможного события
и значит она равна 0. Т.к. F(
=Р(Х<
,
это вероятность достоверного события,
то она равна 1.
5)Функция распределения непрерывна слева
6)функция распределения может иметь не более чем счетного числа скачков
7)Вероятность любого отдельного значения НСВ либо равна 0, либо величине скачка, F(a)=0 или величине скачака.
Т.о всякая функция распределения это непрерывная слева функция неубывающая определенная на всей числовой оси и принимающая значение от 0 до 1.
Любая функция обладающая этими свойствами может быть рассмотрена как функция распределения некоторого НСВ.
БИЛЕТ 28









 a
b
x
a
b
x