
- •Нелинейные системы управления
- •Типовые нелинейности
- •Исследование переходных процессов в нелинейных системах
- •Исследование переходных процессов в нелинейных системах по фазовым портретам
- •Исследование колебательных процессов по фазовым траекториям
- •Метод точечных преобразований
- •Оценка устойчивости колебаний
- •Устойчивость замкнутых нелинейных систем
- •Синтез нелинейных систем
Оценка устойчивости колебаний
 Im
Im
Re
-1/J(A)
WЛ(jω)
Критерий устойчивости сформулирован Гольдфарбом на основании критерия Найквиста следующими рассуждениями:
Рассматривается
линеаризованная система с комплексной
частотной характеристикой ![]()
Если характеристика
проходит через точку ![]() ,
то характеристическое уравнение имеет
чисто мнимые корни, и в замкнутой системе
существуют незатухающие колебания
(например, консервативное звено).
,
то характеристическое уравнение имеет
чисто мнимые корни, и в замкнутой системе
существуют незатухающие колебания
(например, консервативное звено).
Если увеличение
амплитуды колебаний на ![]()
![]() ,
,
где ![]() - амплитуда, при которой характеристика
проходит через точку
- амплитуда, при которой характеристика
проходит через точку
приводит
к уменьшению модуля комплексной частотной
характеристики, т.е. устойчивости
замкнутой системы и переходу мнимых
корней в левую полуплоскость, то появление
множителя ![]() перед
гармонической составляющей уменьшит
амплитуду колебаний. Система вновь
вернется на границу устойчивости с
незатухающими колебаниями. Если при
увеличении на
перед
гармонической составляющей уменьшит
амплитуду колебаний. Система вновь
вернется на границу устойчивости с
незатухающими колебаниями. Если при
увеличении на ![]() ,
модуль КЧХ увеличится, система станет
неустойчивой, мнимые корни перейдут в
правую полуплоскость, амплитуда колебаний
начнет возрастать и вернется к предыдущему
значению
,
модуль КЧХ увеличится, система станет
неустойчивой, мнимые корни перейдут в
правую полуплоскость, амплитуда колебаний
начнет возрастать и вернется к предыдущему
значению ![]() .
.
В системе, обладающей такими свойствами, будут возникать незатухающие автоколебания.
Если ![]() – устойчивые,
– устойчивые,
Если ![]() – неустойчивые.
– неустойчивые.
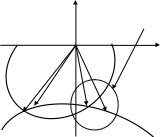 Im
Im
Система устойчива
WЛ(jω) Re
![]()
![]()
![]()
Критерий Гольдфарба
Если увеличение
значения A,
соответствующего некоторому корню
уравнения приводит к выходу кривой
из области ![]() ,
то это решение соответствует устойчивым
автоколебаниям.
,
то это решение соответствует устойчивым
автоколебаниям.
Метод гармонического баланса
Этот метод также используется для приближенной оценки параметров автоколебаний в замкнутой нелинейной системе.
Он основывается на следующих соображениях:
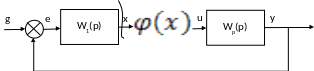
-
Если замкнутую
систему условно разорвать на входе
нелинейного объекта и подать на вход
гармонический сигнал ![]() ,
то в случае, если сигнал, прошедший через
разомкнутую систему, сохранит амплитуду
и фазу (при положительной обратной
связи) или сохранит амплитуду, а фазу
изменит на
,
то в случае, если сигнал, прошедший через
разомкнутую систему, сохранит амплитуду
и фазу (при положительной обратной
связи) или сохранит амплитуду, а фазу
изменит на ![]() (при отрицательной обратной связи), то
в замкнутой системе будут возникать
автоколебания.
(при отрицательной обратной связи), то
в замкнутой системе будут возникать
автоколебания.
![]()
![]()
![]()
![]() ,
,
где ![]() ,
,
![]() - коэффициенты 1-й гармоники ряда Фурье,
- коэффициенты 1-й гармоники ряда Фурье,
- комплексная характеристика нелинейного звена.
![]()
Из условия баланса
![]() :
:
![]()
![]()
![]()
