
- •Синтез систем управления
- •Разомкнутая система с компенсацией возмущения
- •Управление системой с обратной связью
- •Система комбинированного управления
- •Показатели качества регулирования
- •Синтез замкнутых систем управления по ошибке при заданной структуре системы.
- •Синтез системы при произвольной структуре (синтез с корректирующими звеньями)
- •2.Обеспечение устойчивости замкнутой системы.
- •Лекция 14
- •Лекция 15 Синтез замкнутой системы регулирования по корням
Синтез систем управления
Построение законов управления для разомкнутых систем
Структурная схема разомкнутой системы управления содержит объект управления и формирователь управляющего воздействия:
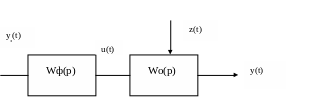
Описание объекта с помощью дифференциального уравнения, записанного в операторной форме, имеет вид:
An(p)*y(t)=Bm(p)*u(t)+Cl(p)*z(t)
Задача системы управления заключается либо в поддержании выходной координаты объекта у на заданном уровне: y(t)=yз , (yз – заданное),
либо в изменении координаты в соответствии с заданным законом: y(t)=yз(t).
yз(t)- y(t)=е(t) – ошибка управления. Если система должна поддерживать управляемую величину на заданном уровне – то эта система называется системой регулирования
Если ошибка управления при любых изменениях yз(t) равна 0,то система называется инвариантной по управлению. Если ошибка равна нулю при любых изменениях возмущения – то система инвариантна по возмущению.
Изменение координаты объекта в соответствии с уравнением объекта определяется зависимостью
![]() ,
,
ошибка управления равна
![]() Для
того, чтобы система была инвариантной,
т.е. ошибка равнялась нулю, управление
нужно формировать в соответствии со
следующим выражением, полученным из
предыдущего при
Для
того, чтобы система была инвариантной,
т.е. ошибка равнялась нулю, управление
нужно формировать в соответствии со
следующим выражением, полученным из
предыдущего при
![]() :
:
![]()
Таким образом, чтобы сформировать управление воздействие из условия инвариантности необходимо иметь математическое описание объектов управления и знать закон изменения задания и возмущения.
Поскольку объектами управления обычно являются инерционные звенья для которых порядок производных у многочлена в левой части больше порядка производной в правой части, то при формировании управляющего воздействия, изменяющего ступенчато, могут возникнуть составляющие управления типа δ – функция.
Пример:
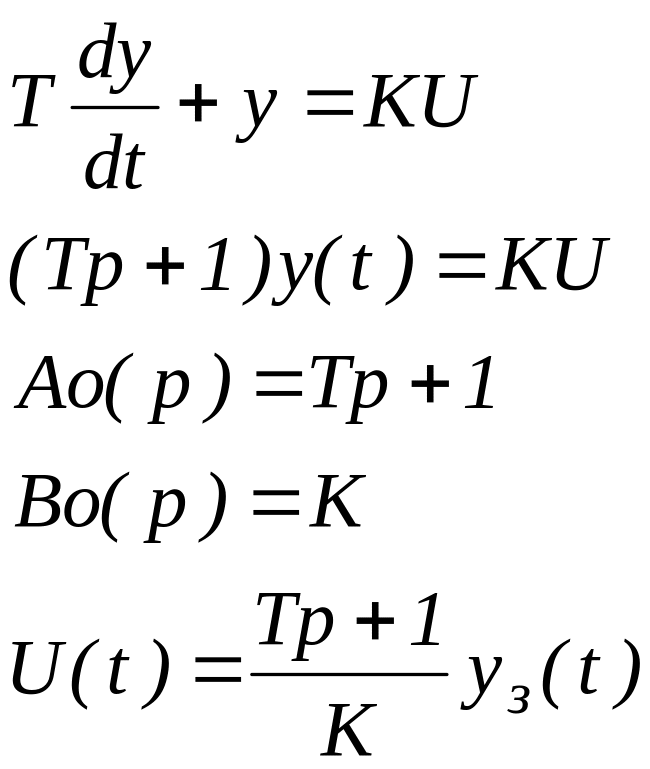
Если yз(t)=1(t)
=>
![]()
Поскольку реально обеспечить управление в виде δ – функции невозможно, инвариантность при таких условиях не обеспечивается.
Если объект не устойчив, то даже небольшие погрешности в оценке задания или возмущения могут привести к очень большим ошибкам.
Пример:
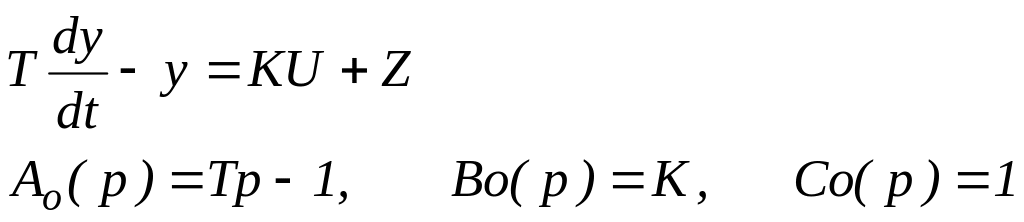
z
– постоянная величина, которую мы знаем
с погрешностью
![]()
Предположим, задание равно нулю и возмущение мы считаем нулевым, следовательно, управление также должно быть нулевым. Но на самом деле возмущение равняется и тогда координата объекта при нулевом управлении будет изменяться по траектории, полученный из решения уравнения:
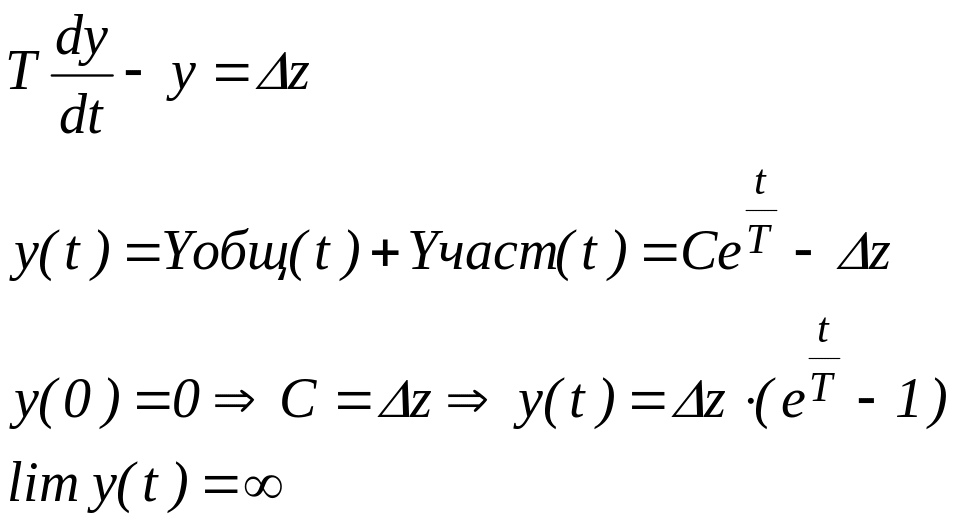
Вывод: Инвариантное уравнение для разомкнутых систем с неустойчивыми объектами невозможно, т.к. даже малые погрешности в оценке задания и возмущения приводят к большим ошибкам, возрастающих в течении времени.
Основными достоинствами разомкнутых систем являются возможность обеспечения инвариантности при определенных условиях и простота системы.
Для того чтобы учесть изменение возмущения во времени необходимо его измерить и формировать управление в соответствии с реально изменяющимся возмущением.
Разомкнутая система с компенсацией возмущения
z*(t)
Wд(р) – передаточная функция датчика, измеряющего возмущение.
Поскольку формирователю управляющего воздействия доступно не само возмущение z(t), а сигнал с выхода датчика, измеряющего возмущение, т.е. z*(t)=Wд(p)z(t), то управляющее воздействие из условия инвариантности должно формироваться в соответствии с выражением
![]() .
.
Чтобы избежать бесконечных изменений управления необходимо ослабить требование функции задания (заменить скочкообразные изменения на более плавные).
Для того, чтобы управлять неустойчивыми объектами их нужно скорректировать путем охвата объекта обратной связью.
