12. Удар абсолютно упругих и неупругих тел.

Ударом (или столкновением) принято называть кратковременное взаимодействие тел, в результате которого их скорости испытывают значительные изменения.

Абсолютно упругий удар – это столкновение двух тел, в результате которого полная механическая энергия тел сохраняется.

(Абсолютно упругий удар — модель соударения, при которой полная кинетическая энергия системы сохраняется.)

Для абсолютно упругого удара выполняется закон сохранения импульса и закон сохранения механической энергии (кинетической энергии). Обозначим скорости шаров массами m1 и m2 до удара через v1 и v2, после удара –v1′ и v2′. В случае прямого центрального удара векторы скоростей шаров лежат на прямой линии, соединяющей их центры. Для взаимодействующих тел имеем:

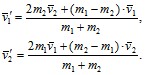
Абсолютно неупругий удар – это столкновение двух тел, в результате которого они объединяются, двигаясь дальше как одно целое.

Если массы шаров m1 и m2, их скорости до удара v1 и v2, то, используя закон сохранения импульса, можем записать:

13. Момент силы и момент импульса.

Момент силы — векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.

1. Момент силы,

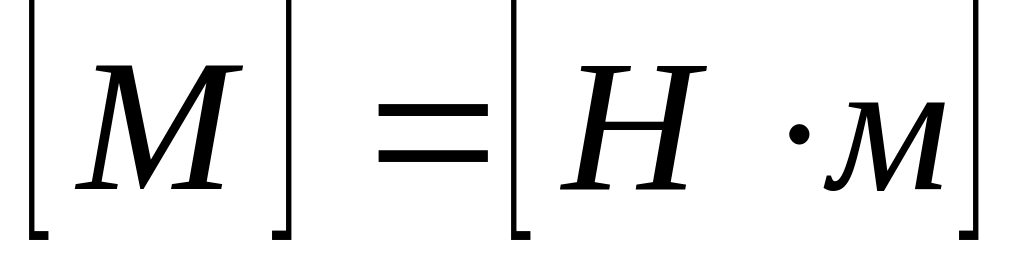
Вектором момента силы относительно полюса называют векторное произведение радиус-вектора и вектора силы: (5)

Н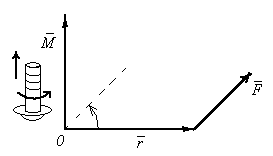 аправление вектора момента силы находится по правилу правого винта (см. рис): перенесем вектор параллельно самому себе так, чтобы совпадали начала векторов и . Если вращать головку винта в направлении от вектора к вектору , то поступательное движение винта укажет направление вектора момента силы .

Модуль вектора момента силы равен:

, (6)

где - угол между радиус-вектором и линией действия силы.

Момент равнодействующей силы относительно полюса О равен геометрической сумме векторов моментов составляющих сил относительно того же полюса:

(7)

или (8)

2. Момент импульса материальной точки,

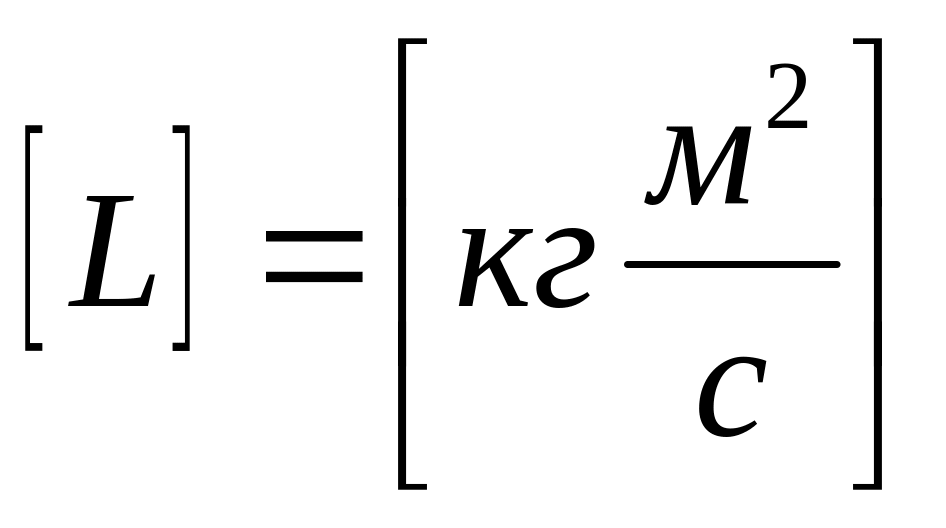
Вектором момента импульса м.т. относительно полюса О называют векторное произведение радиус – вектора и вектора импульса относительно этого же полюса.

Радиус-вектор проводится от полюса О до м. т.

(9)

Направление вектора момента импульса находится по правилу правого винта и совпадает с вектором угловой скорости.

Если учесть, что , тогда момент импульса равен:

или (10)

Момент количества движения твердого тела относительно оси вращения равен произведению момента инерции тела относительно той же оси на угловую скорость.

Модуль вектора момента импульса равен:

, (11)

Вектор момента импульса системы м.т. от-но полюса О равен геометрической сумме векторов моментов импульса, действующих на каждую точку в отдельности от-но того же полюса О:

(12)

или (13)

Моме́нт и́мпульса характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какойскоростью происходит вращение.