10. Кинетическая энергия. Потенциальная энергия материальной точки во внешнем силовом поле. Понятие о градиенте скалярной функции координат.

Физический смысл кинетической энергии: кинетическая энергия тела, движущегося со скоростью υ, показывает, какую работу должна совершить сила, действующая на покоящееся тело, чтобы сообщить ему эту скорость Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела. Кинетическая энергия обозначается буквой E_k.    Тогда равенство (1) можно записать в таком виде: A = E_k2 – E_k1.      (3)

Теорема о кинетической энергии:

работа равнодействующей сил, приложенных к телу, равна изменению кинетической энергии тела.

Так как изменение кинетической энергии равно работе силы (3), кинетическая энергия тела выражается в тех же единицах, что и работа, т. е. в джоулях.

Если начальная скорость движения тела массой т равна нулю и тело увеличивает свою скорость до значения υ, то работа силы равна конечному значению кинетической энергии тела:

Потенциальная энергия тела - это его запасенная энергия. Если тело поднять над землей - у него появится запас энергии. Если его отпустить, запас начнет расходоваться и переходить в кинетическую энергию. Её ещё называют энергией движения

Потенциальная энергия – энергия, обусловленная взаимным расположением тел или частей тела, характеризуется их взаимодействием. При соответствующих условиях возможно изменение потенциальной энергии, за счет чего совершается работа.

Потенциальная энергия находится в поле силы тяжести.

Работа пойдет на увеличение энергии замкнутой системы.

Градиентом скалярной функции называют скорость изменения скалярной функции, взятую в направлении ее наибольшего возрастания. 

Для случая трёхмерного пространства градиентом скалярной функции   координат  ,  ,   называется векторная функция с компонентами

,  ,  .

Или, использовав для единичных векторов по осям прямоугольных декартовых координат  :

Если   — функция   переменных  , то её градиентом называется  -мерный вектор

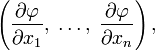
компоненты которого равны частным производным   по всем её аргументам.

11. Закон сохранения энергии в механике. Общефизический закон сохранения энергии.

Закон сохранения энергии в механике: механическая энергия замкнутой консервативной системы не изменяется в процессе ее движения:  Таким образом, в изолированной системе, в которой действуют консервативные силы, механическая энергия сохраняется. В этом состоит закон сохранения механической энергии. Энергия не создается и не уничтожается, а только превращается из одной формы в другую: из кинетической в потенциальную и наоборот.    Учитывая, что в рассматриваемом конкретном случае   и  , можно закон сохранения механической энергии записать так:

или

   Это уравнение позволяет очень просто найти скорость камня v₂ на любой высоте h₂ над землей, если известна начальная скорость v₁ камня на исходной высоте h₁.    Закон сохранения механической энергии легко обобщается на случай любого числа тел и любых консервативных сил взаимодействия между ними. Под E_к нужно понимать сумму кинетических энергий всех тел, а под Е_п - полную потенциальную энергию системы.    Для системы, состоящей из тела массой m и пружины, закон сохранения механической энергии имеет вид

   Полная механическая энергия системы равна сумме ее кинетической и потенциальной энергий. В изолированной системе, в которой действуют только консервативные силы, механическая энергия сохраняется.                                                 

Общефизический закон сохранения энергии: энергия никогда не создаётся и не уничтожается, она может только переходить из одной формы в другую.