8. Механическая система. Центр инерции (масс) механической системы. Теорема о движении центра инерции.

Механическая система – совокупность материальных объектов, которые взаимодействуют друг с другом.

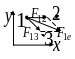- сила воздействия на 1 объект со стороны 2.

Теорема о движении центра масс (инерции): центр масс системы материальных точек движется как материальная точка, в которой сосредоточена масса всей системы и к которой приложены все внешние силы системы.

Теорема имеет закон сохранения. Если главный вектор всех внешних сил системы равен нулю, то есть R_e = 0, то, согласно (15), скорость центра масс остается постоянной, равной его начальной скорости V_C = const = V_0C, причем, если начальная скорость равна нулю, то есть V_0C = 0, то центр масс остается неподвижным.

- сила из вне.

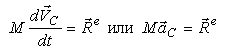
- полный импульс механической системы.

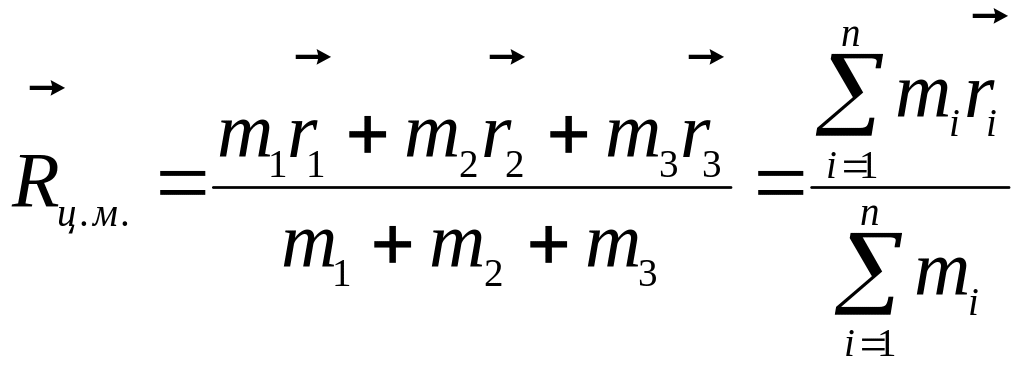
- масса i-той материальной точки.

- радиус-вектор, задающий положение этой материальной точки в пространстве.

- радиус-вектор, задающий положение центра масс.

координаты i-той точечной массы. - орты осей .

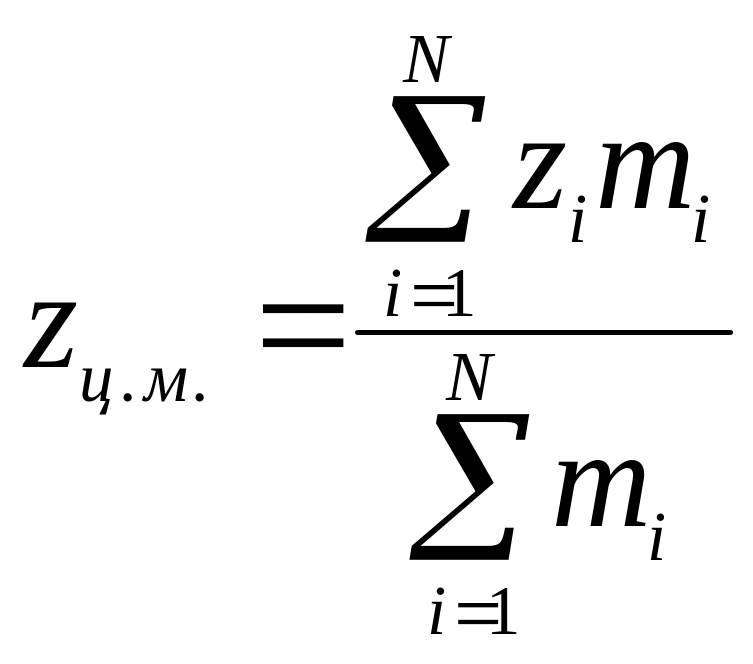
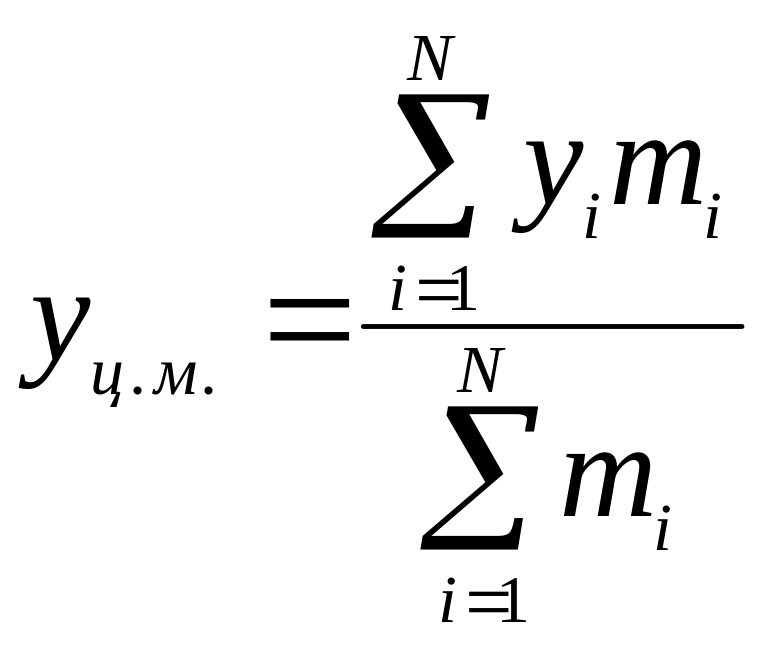
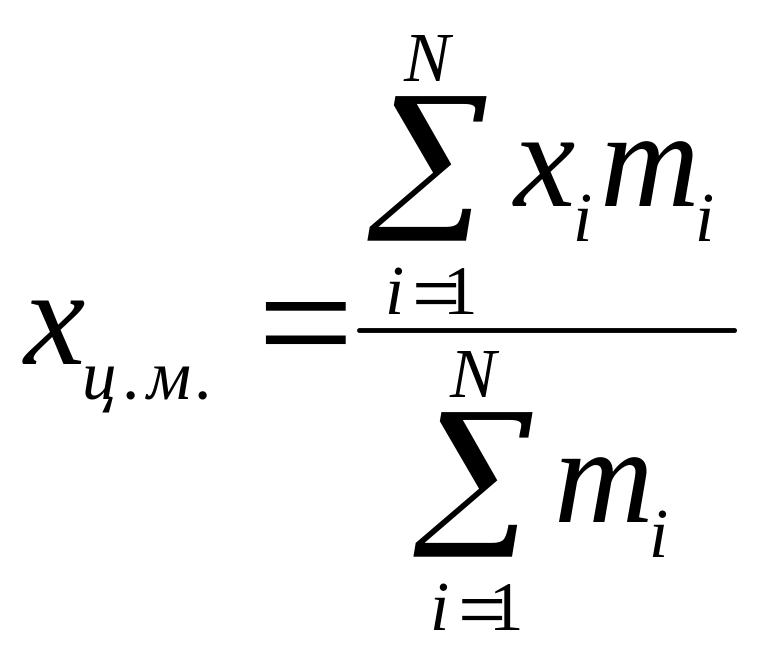
В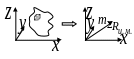 се тело делим на маленькие объемы, и все тело представляем в виде непрерывной совокупности этих кубиков.

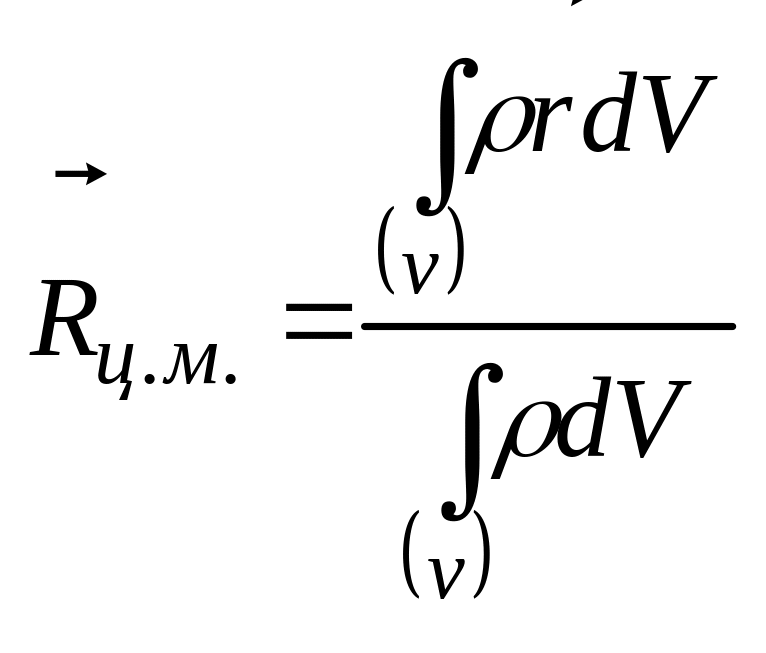
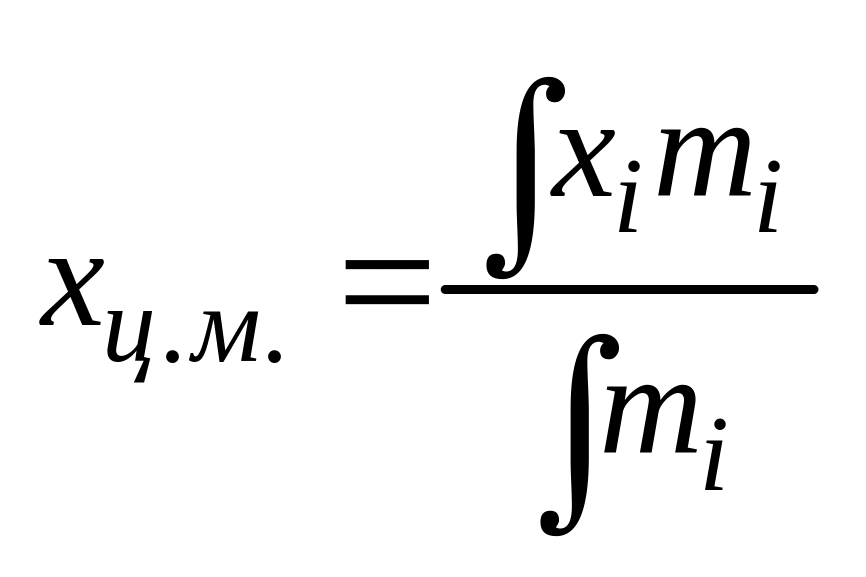
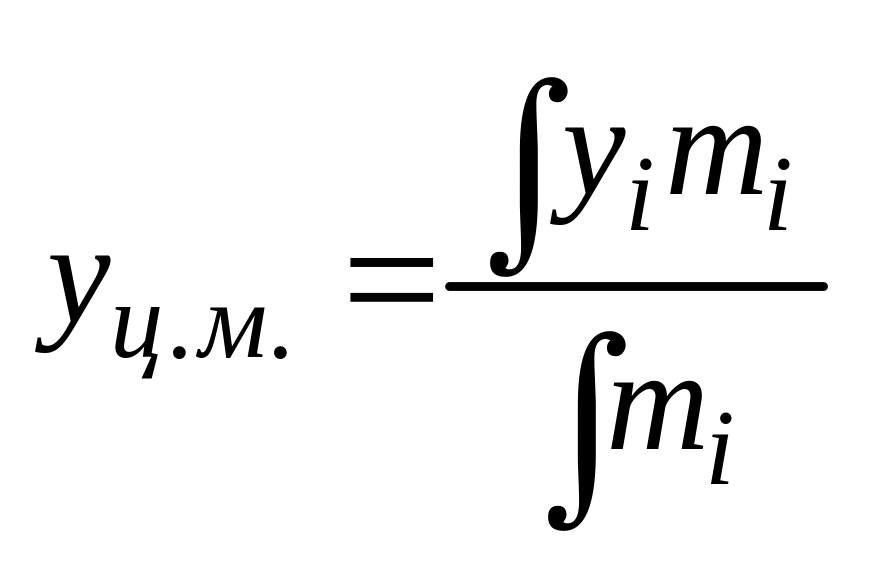
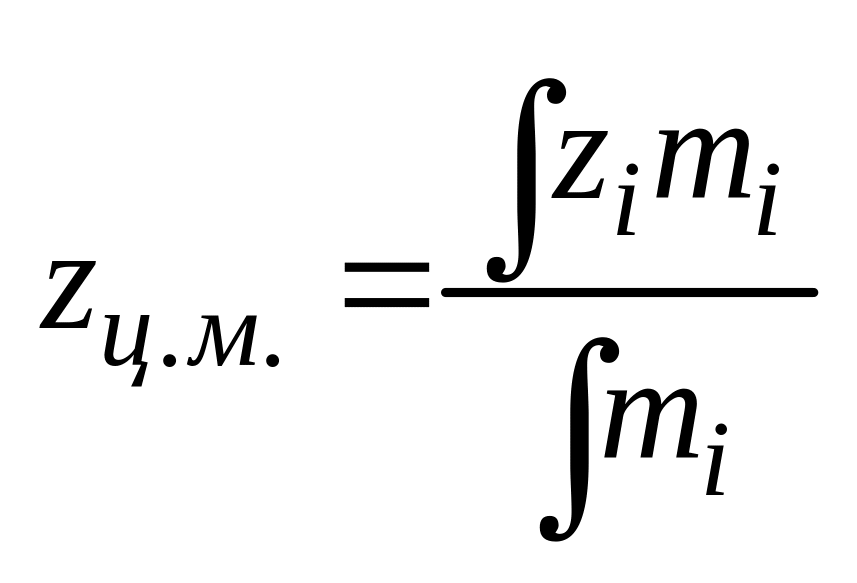
9. Работа силы и её выражение через криволинейный интеграл. Консервативные и неконсервативные силы. Работа силы (сил) над одной точкой

Р абота нескольких сил определяется естественным образом как работа их равнодействующей (их векторной суммы). Поэтому дальше будем говорить об одной силе.

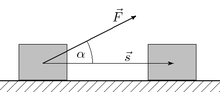
При прямолинейном движении одной материальной точки и постоянном значении приложенной к ней силы работа (этой силы) равна произведению величины проекции вектора силы на направление движения и величины совершённого перемещения:

Здесь точкой обозначено скалярное произведение,   — вектор перемещения; подразумевается, что действующая сила   постоянна в течение всего того времени, за которое вычисляется работа.

Если сила не постоянна, то в этом случае она вычисляется как интеграл:

(подразумевается суммирование по кривой, которая является пределом ломаной, составленной из последовательных перемещений   если вначале считать их конечными, а потом устремить длину каждого к нулю).

Если существует зависимость силы от координат, интеграл определяется следующим образом:

,

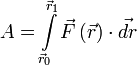где   и   — радиус-векторы начального и конечного положения тела соответственно.

Cледствие: если направление движения тела ортогонально силе, работа (этой силы) равна нулю.

Консервативные и неконсервативные силы

Консервати́вные си́лы (потенциальные силы) — силы, работа которых не зависит от формы траектории (зависит только от начальной и конечной точки приложения сил). Отсюда следует определение: консервативные силы — такие силы, работа которых по любой замкнутой траектории равна 0.

Если в системе действуют только консервативные силы, то механическая энергия системы сохраняется.

Для консервативных сил выполняются следующие тождества:

 — ротор консервативных сил равен 0;

 — работа консервативных сил по произвольному замкнутому контуру равна 0;

 — консервативная сила является градиентом некой скалярной функции  , называемой силовой. Эта функция равна потенциальной энергии   взятой с обратным знаком. Соответственно,   и   связаны соотношением

Таким образом, потенциальная сила всегда направлена против направления возрастания потенциальной энергии.

Примерами консервативных сил являются: сила тяжести, сила упругости. Примерами неконсервативных сил являются сила трения и сила сопротивления среды.