6. Второй закон Ньютона, как уравнение движения. Сила, как производная импульса. Закон сохранения импульса.

Второй закон Ньютона: Изменение количества движения пропорционально приложенной движущей силе и происходит в направлении той прямой, по которой эта сила действует.

В торой закон.

Изменение импульса пропорционально воздействующей на тело силе.

Сила – мера взаимодействия. - импульс (количество движения).

Второй закон Ньютона.

Механическая система – совокупность материальных точек (тел), рассматриваемых как единое целое.

Силы взаимодействия между материальными точками механической системы называются внутренними.

Силы, с которыми на материальные точки системы действуют внешние тела, называются внешними.

М

Закон сохранения импульса тела: импульс тела сохраняется, если импульс равнодействующей всех сил, действующих на это тело, равен нулю. Это возможно в случаях, когда

-на тело не действуют силы вообще или

-равнодействующая всех сил, действующих на тело, равна нулю, или

-промежуток времени, в течение которого мы наблюдаем за состоянием тела, очень мал (стремится к нулю), равнодействующая всех сил, действующих на тело, ограничена по модулю (не бесконечно большая).

еханическая система тел, на которую не действуют внешние силы, называется замкнутой (изолированной).

Импульс – обобщенная мера конкретного движения объекта.

, где - индивидуальная особенность объекта.

- Второй закон Ньютона.

,

Импульс остается неизменным как по величине,

так и по направлению.

Механическая система.

- совокупность из штук объектов.

Рассмотрим механическую систему, состоящую из n тел, масса и скорость которых соответственно равны m₁, m₂, …, m_n и v₁, v₂, …, v_n. Пусть F₁, F₂, …, F_n – равнодействующие внешних сил, а – равнодействующие внутренних сил, действующих на каждое из этих тел. Запишем второй закон Ньютона для каждого из n тел механической системы:

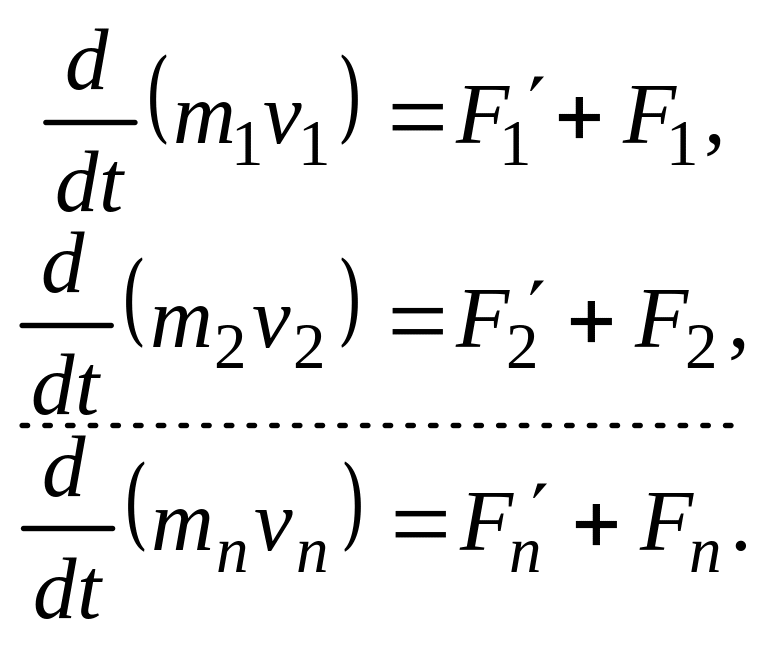Складывая почленно эти уравнения, получаем:

Но так как геометрическая сумма внутренних сил механической системы по третьему закону Ньютона равна нулю, то

или Производная по времени от импульса механической системы равна геометрической сумме внешних сил, действующих на систему.

В случае отсутствия внешних сил (замкнутая система).

7. Третий закон Ньютона.

Третий закон Ньютона: Действие всегда есть равное и противоположное противодействия. Иначе, взаимодействие двух тел друг на друга равны между собой и направлены в противоположные стороны.

При взаимодействии двух тел оба тела получают ускорения, направленные по одной прямой в противоположные стороны. Так как a₁/a₂ = m₂/m₁, то m₁a₁ =m₂a₂, или в векторном виде

m₁а₁ = - m₂a₂.    (1)

Согласно второму закону Ньютона, m₁а₁=F₁ и m₂а₂=F₂. Тогда из формулы (1) следует, что

F₁=-F₂.     (2)

Равенство (2) выражает третий закон Ньютона.

Третий закон.

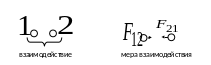
3 закон Ньютона показывает, что силы из-за «взаимного» действия тел друг на друга всегда появляются парами. Если на какое-то тело действует сила, то обязательно есть какое-то другое тело, на которое первое действует такой же по абсолютному значению силой, но направленной в противоположную сторону. Ускорения, которые эти силы сообщают телам, тоже имеют противоположные направления.