
- •Предмет физики. Методы физического исследования. Физические модели. Роль физики в становлении инженера.
- •2. Элементы кинематики материальной точки. Система отсчёта. Радиус-вектор. Скорость и ускорение как производные радиус-вектора по времени. Уравнения движения. Одномерное движение.
- •3. Криволинейное движение. Нормальное и тангенциальное ускорения.
- •4. Элементы кинематики вращательного движения: угловая скорость и угловое ускорение, их связь с линейными скоростями и ускорениями.
- •5. Первый закон Ньютона и понятие инерциальной и неинерциальной системы отсчёта. Масса и импульс. Понятие состояния в классической механике.
- •6. Второй закон Ньютона, как уравнение движения. Сила, как производная импульса. Закон сохранения импульса.
- •7. Третий закон Ньютона.
- •8. Механическая система. Центр инерции (масс) механической системы. Теорема о движении центра инерции.
- •9. Работа силы и её выражение через криволинейный интеграл. Консервативные и неконсервативные силы. Работа силы (сил) над одной точкой
- •10. Кинетическая энергия. Потенциальная энергия материальной точки во внешнем силовом поле. Понятие о градиенте скалярной функции координат.
- •11. Закон сохранения энергии в механике. Общефизический закон сохранения энергии.
- •12. Удар абсолютно упругих и неупругих тел.
- •13. Момент силы и момент импульса.
- •14. Уравнение динамики вращательного движения твёрдого тела.
- •15. Момент инерции материальной точки.
- •16. Момент инерции тела относительно неподвижной оси. Теорема Штейнера.
- •17. Момент импульса механической системы. Закон сохранения момента импульса.
- •18. Кинетическая энергия вращающегося тела.
- •19. Неинерциальные системы отсчёта. Сила инерции. Сила Кориолиса. Основной закон динамики в неинерциальных системах.
- •20. Преобразования Галилея. Механический принцип относительности.
- •21. Постулаты специальной теории относительности.
- •22. Преобразования Лоренца. Относительность длин и промежутков времени. Релятивистский закон сложения скоростей.
- •23. Релятивистский импульс. Основной закон релятивистской динамики материальной точки.
- •24. Взаимосвязь массы и энергии. Соотношение между полной энергией и импульсом частицы. Релятивистское выражение для кинетической энергии.
- •25. Статистический и термодинамический методы исследования.Давление газа с точки зрения мкт
- •26. Уравнение состояния идеального газа
- •27.Средняя кинетическая энергия. Молекулярно кинетическое толкование абсолютной температуры
- •28.Работа газа. Количество теплоты. Теплоемкость
- •30.Число степеней свободы. Закон равномерного распределения энергии по степеням свободы
- •31.Барометрическая формула. Распределение Больцмана
- •32.Принцип детального равновесия. Среднее число столкновений и средняя длина свободного пробега молекул
- •33.Опытные законы диффузии, теплопроводности и внутреннего трения.
- •34.Молекулярно- кинетическая теория явлений переноса в неравновесной системе
- •35. Работа газа при изменении его объема. Внутренняя энергия термодинамической системы.
- •36.Количество теплоты. Первое начало термодинамики. Применение первого начала к изопроцессам
- •37. Теплоемкость. Удельная и молярная теплоемкости. Зависимость теплоемкости идеального газа от вида процесса. Недостаточность классической теории теплоемкости.
- •38.Адиабатный процесс. Уравнение Паусона
- •39. Обратимые и необратимые тепловые процессы. Круговые процессы.
- •40.Цикл Карно и его кпд. Тепловые двигатели и холодильные машины
- •41. Второе начало термодинамики. Приведенная теплота
- •42. Энтропия. Принцип возрастания энтропии. Энтропия идеального газа
- •43. Третье начало термодинамики
- •44. Термодинамическая вероятность. Определение энтропии неравновесной системы через термодинамическую вероятность состояния.
- •45. Силы и потенциальная энергия межмолекулярного взаимодействия. Эффективный диаметр молекул.
- •46.Уравнение Ван-дер-Ваальса. Изотермы Ван-дер-Ваальса и их анализ
- •47. Метастабильные состояния. Критическая тачка. Внутренняя энергия реальных газов
- •48. Понятие фазы, фазового равновесия и превращения. Правила фаз Гиббса
- •49.Фазовый переход первого и второго рода. Диаграммы состояния. Тройная точка.
46.Уравнение Ван-дер-Ваальса. Изотермы Ван-дер-Ваальса и их анализ
Ван-дер-Ваальса уравнение, одно из первых уравнений состояния реального газа, предложенное голландским физиком Я. Д. Ван-дер-Ваальсом (1873):
![]()
Здесь:
р —
давление газа; Т
— его температура;
![]() —
объём одного моля
вещества; R —
универсальная газовая
постоянная;
а и
b — константы,
учитывающие отклонение свойств реального
газа от свойств идеального.
Член
—
объём одного моля
вещества; R —
универсальная газовая
постоянная;
а и
b — константы,
учитывающие отклонение свойств реального
газа от свойств идеального.
Член
![]() ,
имеющий размерность давления, учитывает
притяжение между молекулами газа за
счёт ван-дер-ваальсовых сил (см.
Межмолекулярное
взаимодействие).
Константа b
является поправкой на собственный объём
молекул газа и учитывает отталкивание
молекул на близких расстояниях. Константы
а
и b
обычно определяются из экспериментальных
данных. При больших
можно
пренебречь обеими поправками и В. у.
переходит в уравнение состояния
идеального газа .
,
имеющий размерность давления, учитывает
притяжение между молекулами газа за
счёт ван-дер-ваальсовых сил (см.
Межмолекулярное
взаимодействие).
Константа b
является поправкой на собственный объём
молекул газа и учитывает отталкивание
молекул на близких расстояниях. Константы
а
и b
обычно определяются из экспериментальных
данных. При больших
можно
пренебречь обеими поправками и В. у.
переходит в уравнение состояния
идеального газа .
_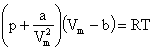 _______________________________________________________________________________________________
_______________________________________________________________________________________________
Для исследования поведения реального газа рассмотрим изотермы Ваи-дер-Ваальса — кривые зависимости р от Vm при заданных Т, определяемые уравнением Ван-дер-Ваальса для моля газа.
Эти кривые (рассматриваются для четырех различных температур) имеют довольно своеобразный характер.
П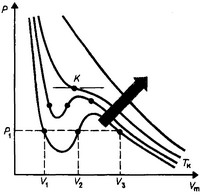
 ри
высоких температурах (Т>Тк)
изотерма реального газа отличается от
изотермы идеального газа только некоторым
искажением ее формы, оставаясь монотонно
спадающей кривой. При некоторой
температуре Тк
на изотерме имеется лишь одна точка
перегиба К - Эта изотерма называется
критической,
соответствующая ей температу- температура
Тк
— критической
температурой.
Критическая изотерма имеет лишь одну
точку перегиба К, называемую критической
точкой; в этой точке
касательная к ней параллельна оси
абсцисс. Соответствующие этой точке
объем Vк
и давление Pк
называются также критическими.
Состояние с критическими параметрами
(Pк
Vк,
Tк)называется
критическим
состоянием. При
низких температурах (Т<ТК) изотермы
имеют волнообразный участок, сначала
монотонно опускаясь вниз, затем монотонно
поднимаясь вверх и снова монотонно
опускаясь.
ри
высоких температурах (Т>Тк)
изотерма реального газа отличается от
изотермы идеального газа только некоторым
искажением ее формы, оставаясь монотонно
спадающей кривой. При некоторой
температуре Тк
на изотерме имеется лишь одна точка
перегиба К - Эта изотерма называется
критической,
соответствующая ей температу- температура
Тк
— критической
температурой.
Критическая изотерма имеет лишь одну
точку перегиба К, называемую критической
точкой; в этой точке
касательная к ней параллельна оси
абсцисс. Соответствующие этой точке
объем Vк
и давление Pк
называются также критическими.
Состояние с критическими параметрами
(Pк
Vк,
Tк)называется
критическим
состоянием. При
низких температурах (Т<ТК) изотермы
имеют волнообразный участок, сначала
монотонно опускаясь вниз, затем монотонно
поднимаясь вверх и снова монотонно
опускаясь.
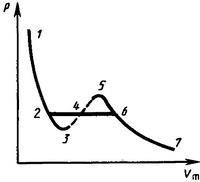
Р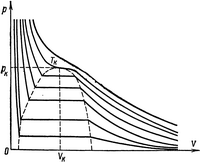 ассматривая
различные участки изотермы при Т<Тк,
видим, что истинная изотерма будет иметь
вид ломаной линии 7—6—2—1.
Часть 7—6
отвечает газообразному состоянию, а
часть 2—1 — жидкому. В состояниях,
соответствующих горизонтальному участку
изотермы 6—2, наблюдается равновесие
жидкой и газообразной фаз вещества.
Вещество в газообразном состоянии при
температуре ниже критической называется
паром, а пар, находящийся в равновесии
со своей жидкостью, называется
насыщенным.
Если
через крайние точки горизонтальных
участков семейства изотерм провести
линию, то получится колоколообразная
кривая, ограничивающая область двухфазных
состояний вещества.
Эта кривая и
критическая изотерма делят диаграмму
р, Vm под изотермой на три области:
ассматривая
различные участки изотермы при Т<Тк,
видим, что истинная изотерма будет иметь
вид ломаной линии 7—6—2—1.
Часть 7—6
отвечает газообразному состоянию, а
часть 2—1 — жидкому. В состояниях,
соответствующих горизонтальному участку
изотермы 6—2, наблюдается равновесие
жидкой и газообразной фаз вещества.
Вещество в газообразном состоянии при
температуре ниже критической называется
паром, а пар, находящийся в равновесии
со своей жидкостью, называется
насыщенным.
Если
через крайние точки горизонтальных
участков семейства изотерм провести
линию, то получится колоколообразная
кривая, ограничивающая область двухфазных
состояний вещества.
Эта кривая и
критическая изотерма делят диаграмму
р, Vm под изотермой на три области:
под колоколообразной кривой располагается область двухфазных состояний (жидкость и насыщенный пар),
слева от нее находится область жидкого состояния,
а справа — область пара.
Пар отличается от остальных газообразных состояний тем, что при изотермическом сжатии претерпевает процесс сжижения. Газ же при температуре выше критической не может быть превращен в жидкость ни при каком давлении.
