43. Третье начало термодинамики

При температуре абсолютного нуля система находится в основном состоянии, которое реализуется одним единственным способом. Следовательно, термодинамическая вероятность  в данном случае равняется 1, а энтропия равняется нулю. Обобщая данное высказывание можно написать следующее выражение, которое является теоремой Нернста или 3 началом термодинамики.

.     (5.11)

При стремлении к нулю абсолютной температуры энтропия термодинамической системы также стремится к нулю

44. Термодинамическая вероятность. Определение энтропии неравновесной системы через термодинамическую вероятность состояния.

Термодинамическая вероятность — число способов, которыми может быть реализовано состояние физической системы. В термодинамике состояние физической системы характеризуется определёнными значениями плотности, давления, температуры и др. измеримых величин. Перечисленные величины определяют состояние системы в целом (её макросостояние). Однако при одной и той же плотности, температуре и т. д. частицы системы могут различными способами распределиться в пространстве и иметь различные импульсы. Каждое данное распределение частиц называется микросостоянием системы. Вероятность термодинамическая (обозначается W) равна числу микросостояний, реализующих данное макросостояние, из чего следует, что . Вероятность термодинамическая связана с одной из основных макроскопических характеристик системы энтропией S соотношением Больцмана: , где  — Больцмана постоянная.

Термодинамическая энтропия S, часто просто именуемая энтропия, в химии и термодинамике является функцией состояния термодинамической системы.

Понятие энтропии было впервые введено в 1865 году Рудольфом Клаузиусом. Он определил изменение энтропии термодинамической системы при обратимом процессе как отношение общего количества тепла к величине абсолютной температуры (то есть тепло, переданное системе, при постоянной температуре):

.

Эта формула применима только для изотермического процесса (происходящего при постоянной температуре) выглядит так:

,

где  — приращение (дифференциал) энтропии некоторой системы, а  — бесконечно малое количество теплоты, полученное этой системой.

Поскольку энтропия является функцией состояния, в левой части равенства стоит её полный дифференциал. Напротив, количество теплоты является функцией процесса, в котором эта теплота была передана, поэтому считать полным дифференциалом нельзя.

Энтропия, таким образом, согласно вышеописанному, определена вплоть до произвольной аддитивной постоянной. Третье начало термодинамики позволяет определить её точнее: предел величины энтропии равновесной системы при стремлении температуры к абсолютному нулю полагают равным нулю.

45. Силы и потенциальная энергия межмолекулярного взаимодействия. Эффективный диаметр молекул.

В нутренняя энергия реального газа складывается из кинетической энергии теплового движения его молекул, которая определяет внутреннюю энергию идеального газа и потенциальную энергию межмолекулярного взаимодействия. Потенциальная энергия реального газа обусловлена только силами притяжения между молекулами. Наличие сил притяжения приводит к возникновению внутреннего давления на газ_

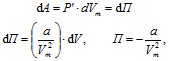
Работа, которая затрачивается на преодоление сил притяжения, действующих между молекулами газа, идет на увеличение потенциальной энергии системы._

г де постоянная интегрирования принята равной нулю. Знак «–» означает, что молекулярные силы, создающие внутреннее давление P′, являются силами притяжения. Учитывая оба слагаемых, получим, что внутренняя энергия моля реального газа_

растет с повышением температуры и увеличением объема.

П ри рассмотрении реальных газов —

газов, свойства которых зависят от взаи­модействия молекул, надо учитывать силы межмолекулярного взаимодействия. Они

проявляются на расстояниях 10^-9 м и быстро убывают при увеличении рассто­яния между молекулами. Такие силы на­зываются короткодействующими.

В XX в., по мере развития представле­ний о строении атома и квантовой механи­ки, было выяснено, что между молекулами вещества одновременно действуют силы притяжения и силы отталкивания. На рис. 88, а приведена качественная зависи­мость сил межмолекулярного взаимодей­ствия от расстояния r между молекулами, где F_o и F_п — соответственно силы оттал­кивания и притяжения, a F — их результи­рующая. Силы отталкивания считаются положительными, а силы взаимного при­тяжения — отрицательными.

Элементарная работа A силы F при увеличении расстояния между молекула­ми на dr совершается за счет уменьше­ния взаимной потенциальной энергии мо­лекул, т. е.

A=Fdr=-dП. (1)

 Эффективный диаметр молекул d - это минимальное расстояние, на которое сближаются при столкновении центры двух молекул. Величина s =p d² называется эффективным сечением молекулы.