
- •Предмет физики. Методы физического исследования. Физические модели. Роль физики в становлении инженера.
- •2. Элементы кинематики материальной точки. Система отсчёта. Радиус-вектор. Скорость и ускорение как производные радиус-вектора по времени. Уравнения движения. Одномерное движение.
- •3. Криволинейное движение. Нормальное и тангенциальное ускорения.
- •4. Элементы кинематики вращательного движения: угловая скорость и угловое ускорение, их связь с линейными скоростями и ускорениями.
- •5. Первый закон Ньютона и понятие инерциальной и неинерциальной системы отсчёта. Масса и импульс. Понятие состояния в классической механике.
- •6. Второй закон Ньютона, как уравнение движения. Сила, как производная импульса. Закон сохранения импульса.
- •7. Третий закон Ньютона.
- •8. Механическая система. Центр инерции (масс) механической системы. Теорема о движении центра инерции.
- •9. Работа силы и её выражение через криволинейный интеграл. Консервативные и неконсервативные силы. Работа силы (сил) над одной точкой
- •10. Кинетическая энергия. Потенциальная энергия материальной точки во внешнем силовом поле. Понятие о градиенте скалярной функции координат.
- •11. Закон сохранения энергии в механике. Общефизический закон сохранения энергии.
- •12. Удар абсолютно упругих и неупругих тел.
- •13. Момент силы и момент импульса.
- •14. Уравнение динамики вращательного движения твёрдого тела.
- •15. Момент инерции материальной точки.
- •16. Момент инерции тела относительно неподвижной оси. Теорема Штейнера.
- •17. Момент импульса механической системы. Закон сохранения момента импульса.
- •18. Кинетическая энергия вращающегося тела.
- •19. Неинерциальные системы отсчёта. Сила инерции. Сила Кориолиса. Основной закон динамики в неинерциальных системах.
- •20. Преобразования Галилея. Механический принцип относительности.
- •21. Постулаты специальной теории относительности.
- •22. Преобразования Лоренца. Относительность длин и промежутков времени. Релятивистский закон сложения скоростей.
- •23. Релятивистский импульс. Основной закон релятивистской динамики материальной точки.
- •24. Взаимосвязь массы и энергии. Соотношение между полной энергией и импульсом частицы. Релятивистское выражение для кинетической энергии.
- •25. Статистический и термодинамический методы исследования.Давление газа с точки зрения мкт
- •26. Уравнение состояния идеального газа
- •27.Средняя кинетическая энергия. Молекулярно кинетическое толкование абсолютной температуры
- •28.Работа газа. Количество теплоты. Теплоемкость
- •30.Число степеней свободы. Закон равномерного распределения энергии по степеням свободы
- •31.Барометрическая формула. Распределение Больцмана
- •32.Принцип детального равновесия. Среднее число столкновений и средняя длина свободного пробега молекул
- •33.Опытные законы диффузии, теплопроводности и внутреннего трения.
- •34.Молекулярно- кинетическая теория явлений переноса в неравновесной системе
- •35. Работа газа при изменении его объема. Внутренняя энергия термодинамической системы.
- •36.Количество теплоты. Первое начало термодинамики. Применение первого начала к изопроцессам
- •37. Теплоемкость. Удельная и молярная теплоемкости. Зависимость теплоемкости идеального газа от вида процесса. Недостаточность классической теории теплоемкости.
- •38.Адиабатный процесс. Уравнение Паусона
- •39. Обратимые и необратимые тепловые процессы. Круговые процессы.
- •40.Цикл Карно и его кпд. Тепловые двигатели и холодильные машины
- •41. Второе начало термодинамики. Приведенная теплота
- •42. Энтропия. Принцип возрастания энтропии. Энтропия идеального газа
- •43. Третье начало термодинамики
- •44. Термодинамическая вероятность. Определение энтропии неравновесной системы через термодинамическую вероятность состояния.
- •45. Силы и потенциальная энергия межмолекулярного взаимодействия. Эффективный диаметр молекул.
- •46.Уравнение Ван-дер-Ваальса. Изотермы Ван-дер-Ваальса и их анализ
- •47. Метастабильные состояния. Критическая тачка. Внутренняя энергия реальных газов
- •48. Понятие фазы, фазового равновесия и превращения. Правила фаз Гиббса
- •49.Фазовый переход первого и второго рода. Диаграммы состояния. Тройная точка.
32.Принцип детального равновесия. Среднее число столкновений и средняя длина свободного пробега молекул
Принцип
детального равновесия
— общее положение статистики,
справедливое для многих случайных
(марковских)
процессов. Его суть заключается в
равенстве вероятностей прямого
![]() и
обратного
и
обратного
![]() переходов
между дискретными состояниями системы
переходов
между дискретными состояниями системы
![]() и
.
и
.
Марковская цепь, для которой выполняется принцип детального равновесия, называется обратимой.
Принцип детального равновесия, в частности, справедлив в приложении к статистической физике и квантовой механике, поскольку он является следствием основных принципов квантовой механики, например, симметрии квантовых уравнений движения относительно обращения времени.
В общем случае, принцип детального равновесия можно сформулировать как равенство вероятностей перехода, отнесённых к конечному состоянию:
![]() ,
,
Где
![]() и
и
![]() —
вероятности того, что система находится
в состояниях
и
,
соответствующие диагональным элементам
матрицы
плотности
—
вероятности того, что система находится
в состояниях
и
,
соответствующие диагональным элементам
матрицы
плотности
![]() ;
;
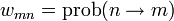 —
вероятность прямого
перехода системы из состояния
в
состояние
;
—
вероятность прямого
перехода системы из состояния
в
состояние
;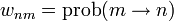 —
вероятность обратного
перехода системы из состояния в состояние
.
—
вероятность обратного
перехода системы из состояния в состояние
.
В отличие от обычного стационарного состояния, для которого достаточно выполнения условия:
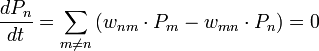 ,
,
детальное равновесие
тр![]() ебует
равенства нулю каждого из членов суммы,
то есть:
ебует
равенства нулю каждого из членов суммы,
то есть:
,
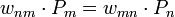 ,
,
Средним числом столкновений молекул идеального газа за одну секунду называется величина, равная <z>=Ö (2)× p d2n<v>. Средней длиной свободного пробега молекул идеального газа называется величина равная l =<v>/<z>=1/(Ö (2)× p d2n).
33.Опытные законы диффузии, теплопроводности и внутреннего трения.
Диффузия) — процесс взаимного проникновения молекул одного вещества между молекулами другого, приводящий к самопроизвольному выравниванию их концентраций по всему занимаемому объёму
Явление
диффузии для химически однородного
газа подчиняется закону
Фука:
![]() где jm
— плотность
потока массы
— величина, определяемая массой вещества,
диффундирующего в
единицу времени через единичную площадку,
перпендикулярную оси х,
D
— диффузия
(коэффициент диффузии),
d/dx
— градиент
плотности, равный скорости изменения
плотности на единицу длины х
в направлении нормали к этой площадке.
Диффузия D
численно равна плотности потока массы
при градиенте плотности, равном единице.
Согласно кинетической теории газов,
где jm
— плотность
потока массы
— величина, определяемая массой вещества,
диффундирующего в
единицу времени через единичную площадку,
перпендикулярную оси х,
D
— диффузия
(коэффициент диффузии),
d/dx
— градиент
плотности, равный скорости изменения
плотности на единицу длины х
в направлении нормали к этой площадке.
Диффузия D
численно равна плотности потока массы
при градиенте плотности, равном единице.
Согласно кинетической теории газов,
![]()
Теплопроводность. Если в одной области газа средняя кинетическая энергия молекул больше, чем в другой, то с течением времени вследствие постоянных столкновений молекул происходит процесс выравнивания средних кинетических энергий молекул, т. е., иными словами, выравнивание температур.
Перенос
энергии в форме теплоты подчиняется
закону Фурье:
![]() (48.1)
(48.1)
где
jE
— плотность
теплового потока
— величина, определяемая энергией,
переносимой в форме теплоты в
единицу времени через единичную площадку,
перпендикулярную оси х,
—
теплопроводность,
![]() —
градиент температуры, равный скорости
изменения температуры на единицу длины
х
в направлении нормали к этой площадке.
Знак минус показывает, что при
теплопроводности энергия переносится
в направлении убывания температуры
(поэтому знаки jE
и
–
противоположны). Теплопроводность
численно равна плотности теплового
потока при градиенте температуры, равном
единице.
—
градиент температуры, равный скорости
изменения температуры на единицу длины
х
в направлении нормали к этой площадке.
Знак минус показывает, что при
теплопроводности энергия переносится
в направлении убывания температуры
(поэтому знаки jE
и
–
противоположны). Теплопроводность
численно равна плотности теплового
потока при градиенте температуры, равном
единице.
Можно
показать, что
![]() (48.2)
(48.2)
где сV — удельная теплоемкость газа при постоянном объеме (количество теплоты, необходимое для нагревания 1 кг газа на 1 К при постоянном объеме), — плотность газа, <v> — средняя скорость теплового движения молекул, <l> — средняя длина свободного пробега.
Внутреннее трение (вязкость). Механизм возникновения внутреннего трения между параллельными слоями газа (жидкости), движущимися с различными скоростями, заключается в том, что из-за хаотического теплового движения происходит обмен молекулами между слоями, в результате чего импульс слоя, движущегося быстрее, уменьшается, движущегося медленнее — увеличивается, что приводит к торможению слоя, движущегося быстрее, и ускорению слоя, движущегося медленнее.
Согласно формуле (31.1), сила внутреннего трения между двумя слоями газа (жидкости) подчиняется закону Ньютона:
![]() (48.5)
(48.5)
где — динамическая вязкость (вязкость), dv/dx — градиент скорости, показывающий быстроту изменения скорости в направлении х, перпендикулярном направлению движения слоев, S — площадь, на которую действует сила F.
Взаимодействие двух слоев согласно второму закону Ньютона можно рассматривать как процесс, при котором от одного слоя к другому в единицу времени передается импульс, по модулю равный действующей силе. Тогда выражение (48.5) можно представить в виде
![]() (48.6)
(48.6)
где
jp
— плотность
потока импульса
— величина, определяемая полным
импульсом, переносимым в единицу времени
в положительном направлении оси х
через единичную площадку, перпендикулярную
оси х,
![]() —
градиент скорости. Знак минус указывает,
что импульс переносится в направлении
убывания скорости (поэтому знаки jр
и
противоположны).
—
градиент скорости. Знак минус указывает,
что импульс переносится в направлении
убывания скорости (поэтому знаки jр
и
противоположны).
Динамическая вязкость численно равна плотности потока импульса при градиенте скорости, равном единице; она вычисляется по формуле
![]() (48.7)
(48.7)
