30.Число степеней свободы. Закон равномерного распределения энергии по степеням свободы

Число степеней свободы: наименьшее число независимых координат, определяющих  положение и конфигурацию молекулы в пространстве.

Модели молекул: а- одноатомной, б- двухатомной, в- трехатомной.

Число степеней свободы для одноатомной молекулы -3 (поступательное движение в направлении трех координатных осей), для двухатомной - 5 ( три поступательных и две вращательных, т.к. вращение вокруг оси Х возможно только при очень высоких температурах),  для трехатомной -6 ( три поступательных и три вращательных).

Итак, средняя энергия приходящаяся на одну степень свободы:

(4.4.1)

У одноатомной молекулы i = 3, тогда для одноатомных молекул

(4.4.2)

для двухатомных молекул

(4.4.3)

для трёхатомных молекул

(4.4.4)

Таким образом, на среднюю кинетическую энергию молекулы, имеющей i-степеней свободы, приходится

(4.4.5)

Это и есть закон Больцмана о равномерном распределении средней кинетической энергии по степеням свободы.

31.Барометрическая формула. Распределение Больцмана

       Атмосферное давление на какой-либо высоте h обусловлено весом слоёв газа, лежащих выше. Пусть P – давление на высоте h , а – на высоте

       Причём, dh >0, а dР < 0, так как на большей высоте давление меньше. Разность давления равна весу газа, заключённого в объёме цилиндра с площадью основания равного единице и высотой dh.

       Т.к. где - плотность газа на высоте h, медленно убывающая с высотой, то можно записать:

.

      Отсюда можно получить барометрическую формулу:

(2.4.1)

где P₀ – давление на высоте h = 0.

       Из формулы (2.4.1) следует, что P убывает с высотой тем быстрее, чем тяжелее газ (чем больше μ) и чем ниже температура (например, на больших высотах концентрация легких газов Не и Н₂ гораздо больше, чем у поверхности Земли).

из основного уравнения молекулярно-кинетической теории: P = nkT, заменим P и P₀ в барометрической формуле (2.4.1) на n и n₀ и получим распределение Больцмана для молярной массы газа:

(2.5.1)

где n₀ и n - число молекул в единичном объёме на высоте h = 0 и h.

       Так как а , то (2.5.1) можно представить в виде

,

(2.5.3)

Больцмана. Здесь n₀ – число молекул в единице объёма там, где U = 0.

Закон Больцмана для распределения частиц идеального газа во внешнем потенциальном поле. n=n₀exp(-e _p/(kT)) Больцман доказал, что это распределение справедливо не только в случае потенциальных сил земного тяготения, но и в любом потенциальном поле сил совокупности любых одинаковых частиц, находящихся в состоянии хаотического движения. В соответствии с этим это распределение было названо законом Больцмана для распределения частиц идеального газа во внешнем потенциальном поле.
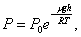