27.Средняя кинетическая энергия. Молекулярно кинетическое толкование абсолютной температуры

Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения.

T = t + 273

Температура — мера средней кинетической энергии молекул.

Средняя кинетическая энергия хаотического движения молекул газа пропорциональна абсолютной температуре.

<E> = m₀<v²>

<v_{кв> =} ²>

Сравнивая уравнение состояния идеального газа и основное уравнение кинетической теории газов, записанные для одного моля (для этого число молекул N возьмём равным числу Авогадро N_А), найдём среднюю кинетическую энергию одной молекулы:

и . N_А=6.02*10²³ моль^-1 R= 8.31 дж/моль*К

Откуда

.           (31)

Средняя кинетическая энергия поступательного движения молекулы не зависит от её природы и пропорциональна абсолютной температуре газа T. Отсюда следует, что абсолютная температура является мерой средней кинетической энергии молекул.

Величина R/N_А = k в уравнении (31) получила название постоянной Больцмана и представляет собой газовую постоянную, отнесенную к одной молекуле:  k = 1,38·10^-23 Дж/К^-23.

Так как = kТ, то средняя квадратичная скорость равна

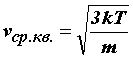
Молекулярно-кинетическое толкование абсолютной температуры.

С точки зрения молекулярно-кинетической теории абсолютная температура есть величина, пропорциональная средней энергии поступательного движения молекулы. <e _пост>=3/2kT.

28.Работа газа. Количество теплоты. Теплоемкость

Работа в термодинамики

А=р∆V (p=const)

A= (p=const)

Q - энергия, которую тело теряет или приобретает при передаче тепла. Формула количества теплоты зависит от протекающего процесса. Формулы количества теплоты при некоторых процессах: Количество теплоты при нагревании и охлаждении. Количество теплоты при плавлении или кристаллизации. Количество теплоты при кипении, испарении жидкости и конденсации пара. Количество теплоты при сгорании топлива. Количество теплоты всегда передается от более горячих тел к более холодным до достижения ими одинаковой температуры (теплового равновесия), если нет иных процессов, кроме теплопередачи. В замкнутой системе тел выполняется уравнение теплового балланса: Q₁ + Q₂ + ... = 0 - количество теплоты, которое теряют горячие тела, равно количеству тепла, получаемому холодными. Полезные формулы: К оличество теплоты, переданное телу, идет на изменение его внутренней энергии и на совершение им работы (Первый закон термодинамики). Закон Джоуля-Ленца: в неподвижном металлическом проводнике вся энергия электрического тока превращается в тепло: - закон Джоуля - Ленца. Q - количество теплоты Дж;

ΔU - изменение внутренней энергии Дж; с - удельная теплоемкость вещества Дж/кг·К;

A' - работа газа Дж m - масса газа кг; T - абсолютная температура газа (t^o + 273) К; С λ - удельная теплота плавления и кристаллизации Дж/кг; r - удельная теплота парообразования и конденсации Дж/кг; q - теплота сгорания топлива Дж/кг; U - напряжение на проводнике В; I - сила тока в проводнике А; R - сопротивление проводника Ом; t - время протекания тока с

ТЕПЛОЕМКОСТЬ, кол-во теплоты, затрачиваемое для изменения т-ры на 1 °С.

где ΔQ - количество теплоты, сообщенное системе и вызвавшее изменение ее температуры на Delta;T. Отношение конечных разностей ΔQ/ΔТ называется средней теплоемкостю, отношение бесконечно малых величин dQ/dT - истинной теплоемкостю.

29.Вероятность и флуктуация. Функция распределения вероятностей. Закон Максвелла для распределения молекул идеального газа по скоростям и энергиям их теплового движения. Средние скорости теплового движения частиц

Вероятностей теория, математическая наука, позволяющая по вероятностям одних случайных событий находить вероятности других случайных событий, связанных каким-либо образом с первыми.

Основные понятия теории вероятностей. Наиболее просто определяются основные понятия Вероятностей теория как математической дисциплины в рамках так называемой элементарной Вероятностей теория Каждое испытание Т, рассматриваемое в элементарной Вероятностей теория, таково, что оно заканчивается одним и только одним из событий E₁, E₂,..., E_S (тем или иным, в зависимости от случая). Эти события называются исходами испытания. С каждым исходом E_k связывается положительное число р_к - вероятность этого исхода. Числа p_k должны при этом в сумме давать единицу. Рассматриваются затем события А, заключающиеся в том, что «наступает или E_i, или E_j,..., или E_k». Исходы E_i, E_j,..., E_k называются благоприятствующими А, и по определению полагают вероятность Р (А) события А, равной сумме вероятностей благоприятствующих ему исходов:   P (A) = p_i + p_s + … + p_k.     (1)   Частный случай p₁ = p₂ =... p_s = 1/S приводит к формуле   Р (А) = r/s.     (2)   Формула (2) выражает так называемое классическое определение вероятности, в соответствии с которым вероятность какого-либо события А равна отношению числа r исходов, благоприятствующих А, к числу s всех «равновозможных» исходов. Классическое определение вероятности лишь сводит понятие «вероятности» к понятию «равновозможности», которое остаётся без ясного определения.

Флуктуации (от лат. fluctuatio – колебание), случайные отклонения наблюдаемых физических величин от их средних значений. Флуктуации происходят у любых величин, зависящих от случайных факторов и описываемых методами статистики Количественная характеристика Флуктуации основана на методах математической статистики и вероятностей теории. Простейшей мерой Флуктуации величины х служит её дисперсия s²_x, т. е. средний квадрат отклонения х от её среднего значения , s²_x = , где черта сверху означает статистическое усреднение. Флуктуации справедливо и в случае квантовой статистики, различаются лишь явные выражения для C_V. 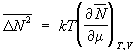Для систем с постоянным объёмом в контакте с термостатом и резервуаром частиц большое каноническое распределение Гиббса даёт для Флуктуации числа частиц: , где m – химический потенциал. В приведённых примерах флуктуируют пропорциональные объёму (т. н. экстенсивные) величины.

Закон Максвелла для распределения молекул идеального газа по скоростям теплового движения. В 1860 году Максвелл теоретически установил распределение молекул идеального газа по скоростям теплового движения и записал в виде F(v)=f(v)4p v² и позже получил то, что впоследствии назвал формулой распределения молекул идеального газа по скоростям теплового движения. Она имеет вид F(v)=(m/(2p kT))^3/2exp(-mv²/(2kT))4p v². Вероятностное толкование закона распределения Максвелла. Выражение dN_v=Nf(v)4p v²dv даёт число молекул, величина скоростей которых лежит в интервале от v до v+dv. Разделив его на n получим вероятность того, что скорость молекулы окажется между v и v+dv, то есть dP_v=f(v)4p v²dv.

Средняя скорость теплового движения частицы вычисляется по формуле v=√ (3kT/m)

(m — масса броуновской частицы, v — ее скорость, k — постоянная Больцмана, T — температура