25. Статистический и термодинамический методы исследования.Давление газа с точки зрения мкт

Молекулярная физика и термодинамика — разделы физики, в которых изучаются макроскопические процессы в телах, связанные с огромным числом содержащихся в телах атомов и молекул. Для исследования этих процессов применяют два качественно различных и взаимно допол­няющих друг друга метода: статистический (молекулярно-кинетический) и термодинами­ческий. Первый лежит в основе молекулярной физики, второй — термодинамики.

Молекулярная физика — раздел физики, изучающий строение и свойства вещества исходя из молекулярно-кинетических представлений, основывающихся на том, что все тела состоят из молекул, находящихся в непрерывном хаотическом движении.

Термодинамика — раздел физики, изучающий общие свойства макроскопических систем, находящихся в состоянии термодинамического равновесия, и процессы перехо­да между этими состояниями.

Макроскопическое состояние (или макросостояние) — это состояние системы, характеризуемое небольшим числом величин давления Р, температуры Т, объема V и, быть может, еще нескольких других существенных характеристик.

Уравнение можно записать в виде:

Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака:

— закон Бойля — Мариотта.

— закон Гей-Люссака.

— закон Шарля

Давление газа с точки зрения молекулярно-кинетической теории

Давление - это явление когда частицы (молекулы) "давят" на сосуд (под действием внутренней энергии и теплового беспорядочного движения ударяются в стенки сосуда). Чем больше кинетическая энергия частицы тем больше сила удара об стенку приходящаяся на единицу площади, тем больше давление.

26. Уравнение состояния идеального газа

Идеальным газом называется газ, молекулы которого являются материальными точками, то есть расстояния между молекулами намного превосходят их размеры, а единственный вид их взаимодействий между собой - упругие механические столкновения.

Состояние данной массы газа полностью определено, если известны его давление, температура и объем. Эти величины называют параметрами состояния газа. Уравнение, связывающее параметры состояния, называют уравнением состояния.          Для произвольной массы газа состояние газа описывается уравнением Менделеева—Клапейрона: pV = mRT/M, где р — давление, V — объем, m — масса, М — молярная масса, R — универсальная газовая постоянная. Физический смысл универсальной газовой постоянной в том, что она показывает, какую работу совершает один моль идеального газа при изобарном расширении при нагревании на 1 К (R = 8,31 ДжДмоль • К)).          Уравнение Менделеева—Клапейрона показывает, что возможно одновременное изменение трех параметров, характеризующих состояние идеального газа. Однако многие процессы в газах, происходящие в природе и осуществляемые в технике, можно рассматривать приближенно как процессы, в которых изменяются лишь два параметра. Особую роль в физике и технике играют три процесса: изотермический, изохорный и изобарный.          Изопроцессом называют процесс, происходящий с данной массой газа при одном постоянном параметре — температуре, давлении или объеме. Из уравнения состояния как частные случаи получаются законы для изопроцессов.          Изотермическим называют процесс, протекающий при постоянной температуре. Т = const. Он описывается законом Бойля—Мариотта: pV = const.          Изохорным называют процесс, протекающий при постоянном объеме. Для него справедлив закон Шарля: V = const, p/T = const.          Изобарным называют процесс, протекающий при постоянном давлении. Уравнение этого процесса имеет вид V/T = const при р = const и называется законом Гей-Люссака. 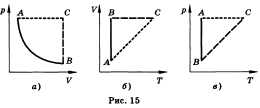Все процессы можно изобразить графически (рис. 15).          Реальные газы удовлетворяют уравнению состояния идеального газа при не слишком высоких давлениях (пока собственный объем молекул пренебрежительно мал по сравнению с объемом сосуда,                     в котором находится газ) и при не слишком низких температурах (пока потенциальной энергией межмолекулярного взаимодействия можно пренебречь по сравнению с кинетической энергией теплового движения молекул), т. е. для реального газа это уравнение и его следствия являются хорошим приближением.