2.2.2 Метод неканонических разложений

Метод неканонических разложений применяется для уменьшения основного недостатка метода канонических разложений (большой требуемый объем машинных ресурсов) при сохранении главного достоинства  возможности цифрового моделирования случайного процесса для заранее неизвестных отсчетов времени.

При неканоническом представлении модель случайного процесса задается в виде нелинейной функции, зависящей от малого числа случайных параметров. Разработано несколько таких представлений, позволяющих моделировать стационарные случайные процессы с заданной корреляционной функцией (спектральной плотностью мощности). При этом легко может быть обеспечено заданное математическое ожидание случайного процесса с использованием соотношения (2.2).

Один из возможных методов заключается в представлении случайного процесса (с нулевым средним) в виде

(2.33)

где случайные параметры.

Так как моделируется случайный процесс с заданной корреляционной функцией, то фаза имеет равномерную плотность вероятности

(2.33а)

Случайная величина , равная частоте реализации, должна быть определена так, чтобы при усреднении по ансамблю всех возможных реализаций модели (2.33), спектральная плотность мощности модели совпадала с заданной спектральной плотностью мощности (2.22). Отсюда следует, что плотность вероятности параметра должна равняться

(2.33б)

где деление на введено для нормировки , которая как плотность вероятности должна соответствовать условию .

Модель (2.33) соответствует случайному процессу с нулевым средним. Если же необходимо моделировать процесс с ненулевым средним, то можно использовать соотношение (2.2).

Случайная величина , равная амплитуде гармоники (2.33), может выбираться исходя из различных соображений. В частности, плотность распределения вероятности можно выбрать произвольной, так как для моделируемого процесса плотность вероятности не задана. При этом величина должна быть положительной, а ее мощность определяться мощностью моделируемого случайного процесса, т.е. , где дисперсия моделируемого случайного процесса.

Еще один вариант задания вероятностных характеристик случайного параметра рассмотрен в разд. 3.

Конечно, существует "плата" за отказ от математически строгого представления случайного процесса в виде канонического разложения. Эта "плата" состоит в том, что процесс, представленный в виде неканонического разложения (2.33), стационарен, но не является эргодическим. Одна реализация случайного процесса (2.33) не представляет весь ансамбль реализаций случайных процессов, имеющих заданную корреляционную функцию или спектральную плотность мощности . В самом деле, спектральная плотность мощности одной й реализации процесса (2.33) отлична от нуля лишь на частотах, близких к частоте , соответствующей этой реализации, а корреляционная функция этой реализации является периодической функцией (косинусоидой) с периодом . Этот факт иллюстрируется на рис. 2.1, где а - реализации случайного процесса, генерируемого в соответствии с (2.33), а б - реализация эргодического процесса. Моделирование с использованием случайного процесса, не являющегося эргодическим, может потребовать большего времени, так как для достоверной статистической оценки его воздействия на моделируемую систему или устройство необходимо произвести большое количество испытан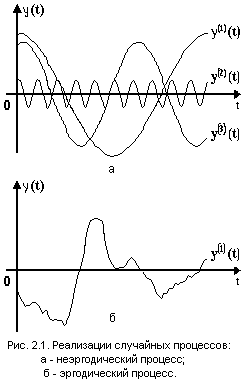 ий, а во многих ситуациях это заставит отказаться от модели (2.33).

Необходимо отметить, что не все канонические представления случайных процессов обладают эргодичностью. Так, например, каждая реализация случайного процесса с использованием канонического разложения (2.24) содержит гармоники со случайными, но фиксированными для каждой конкретной реализации амплитудами гармоник, равными , совпадающими с заданной спектральной плотностью мощности на частоте . В то же время разложение (2.31) дает реализации случайного процесса, обладающие эргодическим свойством, так как амплитуды в каждой реализации определяются точно по энергетическому спектру в соответствии с (2.32) и (2.28).

Ослабить (но не устранить полностью) недостатки представления (2.33), связанные с неэргодичностью, позволяет представление

(2.34)

где случайные параметры, имеющие такие же вероятностные характеристики, что и в модели (2.33). Очевидно, что при увеличении неканоническое разложение (2.34) приближается к каноническому (2.24) как по свойствам моделируемых процессов, так и по затратам машинных ресурсов.