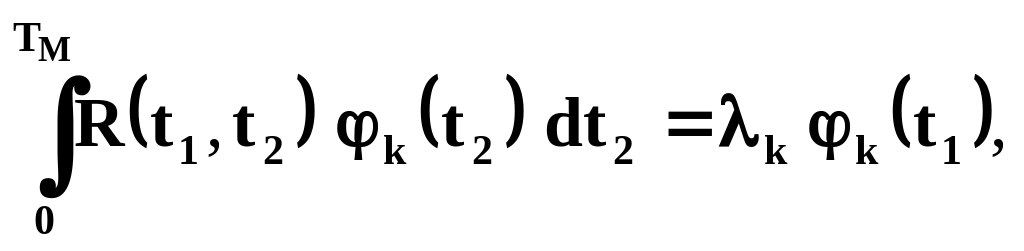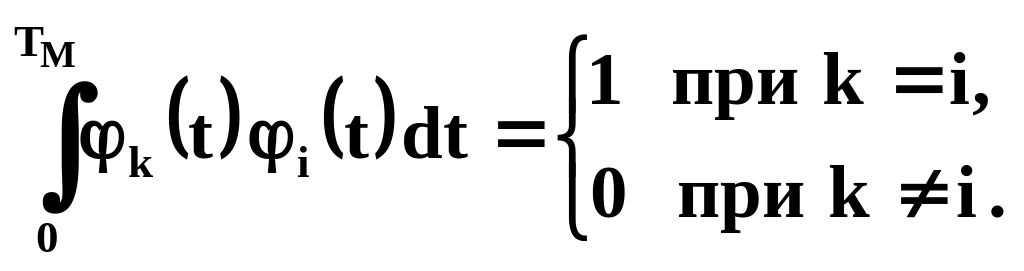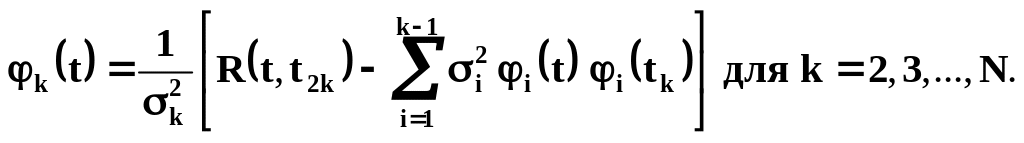2.1.2. Метод канонических разложений

В этом методе используется разложение случайного процесса в ряд:

(2.11)

где коэффициенты разложения; детерминированные функции, образующие систему функций.

Коэффициенты разложения  случайные величины, изменяющиеся от реализации к реализации. Для того чтобы при моделировании по (2.11) можно было бы использовать в качестве реализации независимых чисел, необходимо, чтобы были некоррелированными, т.е.

(2.12)

При этом целесообразно полагать, что

(2.13)

и, если необходимо моделировать случайный процесс с ненулевым средним, то можно воспользоваться соотношением (2.2).

Условию некоррелированности случайных коэффициентов в (2.11) нельзя удовлетворить при произвольном выборе системы функций . Оказывается, что некоррелированность обеспечивается при выборе в качестве системы всех функций, являющихся решениями интегрального уравнения

(2.14)

где  заданная корреляционная функция,  интервал моделирования случайного процесса,  собственные числа уравнения (2.14).

Функция , удовлетворявшая уравнению (2.14), называется собственной функцией этого интегрального уравнения.

Если положить, что

(2.15)

то функции , используемые в разложении (2.11), являются ортонормированными:

(2.16)

Таким образом, использование в качестве системы функций всех возможных решений интегрального уравнения (2.14) и случайных коэффициентов , удовлетворяющих условиям (2.12), (2.14) и (2.15), позволяет применять при моделировании датчики случайных величин и затем линейное преобразование, соответствующее каноническому разложению (2.11). Это является следствием известной теоремы Карунена-Лоева.

Основным достоинством метода канонических разложений является возможность моделирования случайного процесса для любого момента времени , а не для набора дискретных моментов времени, как при методе линейного преобразования. Это оказывается возможным, потому что случайный процесс моделируется как функция непрерывного времени в соответствии с (2.11).Однако метод канонических разложений применяется в описанном виде очень редко из-за присущих ему недостатков, заключающихся в следующем.

Во-первых, в соответствии с (2.11) необходимо использовать бесконечное число функций , случайных коэффициентов и бесконечное число арифметических операций, что не может быть реализовано при цифровом моделировании. Практически число членов ряда (2.11) при цифровом моделировании берется конечным и возникает методическая ошибка, которая тем меньше, чем больше число членов в используемом усеченном ряде (2.11).

Во-вторых, более существенным недостатком метода канонических разложений является то, что решение интегральных уравнений (2.14) может быть аналитически найдено лишь для ограниченного вида корреляционных функций .

В связи с этим обычно применяются приближенные методы канонических разложений, одним из которых является метод, предложенный В.С. Пугачевым. Метод В.С. Пугачева заключается в следующем. Вместо случайного процесса с заданной корреляционной функцией моделируется случайный процесс с корреляционной функцией , связанной с заданной как

.

(2.17)

Из этого следует, что корреляционные функции и совпадают лишь для дискретных моментов времени; полного совпадения и нет, но при определенном выборе дискретных точек на временной оси корреляционная функция моделируемого процесса приближенно равна заданной :

.

(2.18)

Таким образом, основное преимущество метода канонических разложений по отношению к методу линейного преобразования сохраняется, но возникает методическая ошибка из-за несовпадения корреляционных функций (2.18). Моделирование происходит по формуле

,

(2.19)

где в отличие от разложения (2.11) конечное число слагаемых, равное числу дискретных точек, на которых выполняется (2.17),что позволяет экономить память и уменьшает число требуемых элементарных операций при программной реализации метода.

Подготовительная работа состоит в выборе системы ортонормированных функций и определении требований к некоррелированным случайным величинам . Как и при использовании канонического разложения (2.11), предъявляются требования лишь к первому и второму моментам случайных величин , при этом среднее равно нулю: , а дисперсии случайных величин и функции , как показал В.С. Пугачев, могут быть найдены по рекуррентным формулам:

	(2.20)

Итак, ещё одним достоинством метода В.С. Пугачева по сравнению с использованием канонического разложения (2.11) является отсутствие необходимости решения интегрального уравнения (2.14) при нахождении системы функций , для которых записывается разложение. В данном случае все функций определяются на основе простых алгебраических преобразований (2.20), которые легко могут быть запрограммированы.

Известно, что отличие от заданной уменьшается при увеличении числа дискретных точек и таком выборе этих точек на временной оси, когда заданная в этих точках принимает наибольшее значение.