2.1. Моделирование нестационарных процессов с заданными корреляционными свойствами

Если моделируемый случайный процесс с заданными корреляционными свойствами нестационарен, то его корреляционная функция зависит от двух аргументов: , знак математического ожидания.

При моделировании случайного процесса обычно полагается, что он имеет нулевое математическое ожидание:

,

(2.1)

поскольку при необходимости моделировать процесс с ненулевым математическим ожиданием

,

(2.2)

если удовлетворяет (2.1), а заданное математическое ожидание .

Если моделирование случайного процесса необходимо осуществить для дискретных заранее известных моментов времени то, как и в разд. 1, моделирование случайного процесса может быть сведено к моделированию случайного вектора с составляющими. В рассматриваемом случае моделирования для случайного вектора известна корреляционная матрица, элементы которой равны .

2.1.1. Метод линейного преобразования

Этот метод используется для моделирования отсчетов случайного процесса с заданной корреляционной функцией в дискретные, заранее известные моменты времени, не обязательно равноотстоящие.

Идея метода заключается в линейном преобразовании некоррелированного вектора в коррелированный вектор . Некоррелированный вектор имитируется с помощью датчиков случайных чисел:

Вектор , представляющий моделируемый случайный процесс, формируется из с помощью линейного преобразования  умножения на матрицу :

,

(2.3)

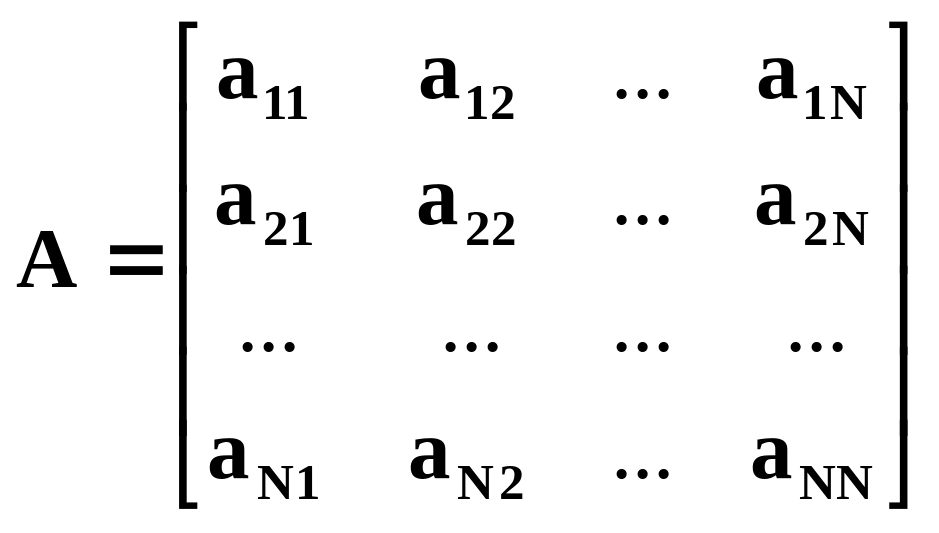
где  квадратная матрица преобразования.

Очевидно, что элементы матрицы должны быть определены по заданным .

Хотя большинство используемых методов моделирования процессов с заданными корреляционными свойствами используют линейные преобразования, название “метод линейного преобразования” в литературе закрепилось за рассматриваемым методом.

Пусть используется датчик случайных чисел, обеспечивающий математическое ожидание , равное нулю, и дисперсию , равную единице, т.е.

.

(2.4)

Кроме того, из-за независимости случайных величин, генерируемых датчиком случайных чисел, выполняется условие некоррелированности для составляющих вектора :

(2.5)

Условия (2.4) и (2.5) легко реализуются.

Матрица по заданной может быть определена различными способами. Наиболее простым является следующий.

Решение задачи нахождения матрицы становится единственным и наиболее простым, если считать матрицу нижней треугольной:

.

(2.6)

В этом случае компоненты векторов и в соответствии с (2.3) связаны следующим образом:

.

В соответствии с этим можно выразить корреляционные моменты отсчетов случайного процесса через элементы с учетом (2.4) и (2.5).

Определим, например, следующие коэффициенты корреляции:

и так далее.

Из этих уравнений легко определяются коэффициенты матрицы по заданным :

	(2.7)
	(2.8)
	(2.9)
	(2.10)

После определения вычисление элементов матрицы осуществляется по строкам (2.6). Сначала по (2.8) находится первый элемент очередной строки, затем по (2.9) определяются все элементы этой строки, кроме последнего ненулевого, и затем вычисляется последний ненулевой элемент в каждой очередной строке по (2.10). Таким образом, вычисление элементов матрицы может быть легко осуществлено в соответствии с формулами (2.7)(2.10).Моделирование осуществляется по (2.3).

Необходимо отметить, что в требования к датчику случайных чисел (2.4) и (2.5) не включено требование к закону распределения. Закон распределения в соответствии с этим может быть произвольным; обычно используется равномерное распределение для датчиков случайных величин , при этом плотность вероятности моделируемого процесса не оговаривается. Если же моделируется нормальный случайный процесс, то и случайные величины также должны быть распределены по нормальному закону; в этом случае и будут подчиняться нормальному распределению, так как это распределение не видоизменяется при линейном преобразовании.

При моделировании стационарных процессов с заданными корреляционными свойствами метод линейного преобразования применять можно, но нецелесообразно, так как в этом случае рационально использовать эффективные, разработанные специально для этой ситуации методы.

Если моделируемый случайный процесс имеет ненулевое математическое ожидание, то необходимо использовать соотношение (2.2).
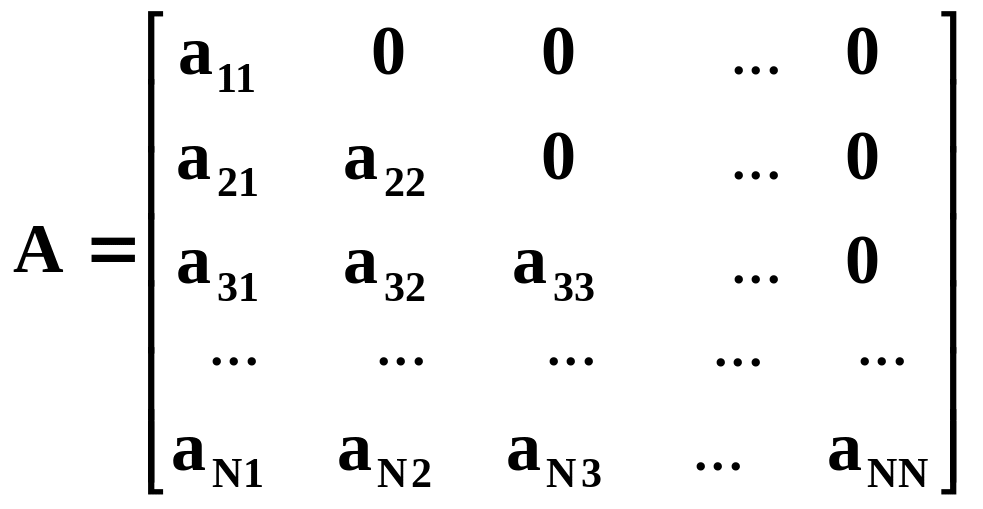