1.3. Моделирование марковских случайных процессов

Во многих радиотехнических приложениях случайные процессы описываются как марковские случайные процессы. Моделирование марковских процессов легко осуществляется на основе метода условных распределений (см. разд. 1.1). Рассмотрим моделирование марковских процессов на примере марковских процессов первого порядка.

Для марковского процесса первого порядка условные вероятности для каждого значения процесса в момент времени зависят, как это следует из формального определения, лишь от значения отсчета процесса в предыдущий момент времени , т.е. в отличие от (1.5):

Э та условная вероятность называется вероятностью перехода, обычно она задается при моделировании.

Таким образом, в отличие от общего случая применения метода условных распределений для расчета условных плотностей вероятностей при подготовительной работе не требуется. Кроме того, вероятность перехода, представляющая условную плотность вероятности, для каждого такта моделирования зависит, в случае марковского процесса первого порядка, лишь от одного значения процесса в предыдущий такт времени , что упрощает моделирование и программирование.

При моделировании марковского процесса задается также плотность вероятности (1.4) начального значения процесса в момент времени .

Многомерная плотность вероятности, характеризующая марковский процесс, записывается как

.

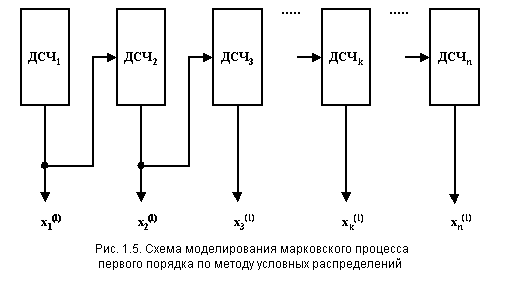
Таким образом, моделирование марковского процесса может происходить по схеме, показанной на рис. 1.5, где в отличие от схемы рис. 1.3, соответствующей общему случаю, уменьшается количество связей.

Моделирование марковских процессов, имеющих более высокий порядок, принципиально не отличается от моделирования марковских процессов первого порядка; для марковских процессов го порядка вероятность перехода зависит от предыдущих значений процесса, .

Моделирование стационарных марковских процессов упрощается, так как вероятности перехода в этом случае не зависят от момента времени (при ). В этом случае существенно уменьшение требуемой памяти при моделировании.

Стационарный марковский процесс с нормальной вероятностью перехода является нормальным процессом с дробнорациональной спектральной плотностью мощности. Поэтому для моделирования марковских процессов могут быть использованы методы моделирования нормальных процессов, так же, как для моделирования нормального процесса можно использовать метод условных распределений.

2. Моделирование случайных процессов с заданными корреляционными свойствами

На практике часто возникает необходимость моделирования случайных процессов с известными, т.е. заданными, корреляционными свойствами, при этом другие статистические характеристики процесса не заданы. Так, например, может быть неизвестна такая важная характеристика случайного процесса, как одномерная плотность вероятности. Неизвестны при этом совместные плотности вероятности отсчетов случайного процесса, моменты более высокого порядка, чем второй, и другие характеристики. Такая ситуация распространена по следующим причинам:

1. Если моделируется нормальный (гауссов) случайный процесс, то для его описания, как известно, достаточно знать корреляционную функцию. Так как в приложениях нормальные случайные процессы используются чаще, чем какиелибо другие случайные процессы, то методы моделирования случайных процессов по заданным корреляционным функциям находят очень широкое применение.

2. Часто в радиотехнических приложениях необходимо моделировать негауссовы случайные процессы, которые легко (без больших затрат машинного времени и при несложной подготовительной работе) могут быть сформированы из нормальных процессов. Нормальные же процессы, как указывалось выше, можно моделировать как процессы с заданной корреляционной функцией.

3. На практике при моделировании негауссова случайного процесса может быть известна лишь корреляционная функция процесса. Такая ситуация возникает, например, при моделировании случайного процесса по экспериментальным данным; при эксперименте часто не удается определить другие характеристики случайного процесса. Очень часто и при теоретическом описании случайного процесса также не удается установить какие-либо его характеристики, кроме корреляционных.

4. При моделировании может возникать ситуация, когда конечный результат моделирования зависит лишь от корреляционных свойств моделируемого случайного процесса. Например, если моделируемый случайный процесс воздействует на линейное инерционное устройство, то, как известно, при этом происходит нормализация случайного процесса, и характеристики случайного процесса на выходе полностью определяются только корреляционными свойствами исходного случайного процесса.