Синтез рекурсивного формирующего фильтра с нулевой методической погрешностью для корреляционной функции

Синтез рекурсивного формирующего фильтра с нулевой методической погрешностью может быть осуществлен по аналоговому формирующему фильтру (2.84), т.е. для случая, когда заданная спектральная плотность мощности является дробно-рациональной функцией частоты.

Рассмотрим идею синтеза таких формирующих фильтров на примере. Пусть требуется построить рекурсивный формирующий фильтр для моделирования случайного процесса с корреляционной функцией и спектральной плотностью мощности .

Как показано в примере 2.5, передаточная функция аналогового формирующего фильтра в этом случае должна быть ,

а импульсная характеристика этого фильтра выражается как

.

Этот аналоговый фильтр можно использовать в схеме рис. 2.2. При этом для выходного сигнала (моделируемого процесса) можно записать

(2.86)

Это выражение  интеграл Дюамеля, связывающий входное воздействие формирующего фильтра с его реакцией .

Выразим значение реакции формирующего фильтра в момент времени через реакцию в момент времени (2.86):

	(2.87)

Рассмотрим первое слагаемое в этом выражении.

Вынося за скобки и возвращаясь к записи через , получаем

(2.88)

Второе слагаемое статистически независимо от первого, так как оно равно результату действия на формирующий фильтр входного белого шума на временном интервале , не перекрывающемся с интервалом для первого слагаемого. Эта статистическая независимость определена тем, что для белого шума любые его значения в несовпадающие моменты времени независимы. Исчерпывающей статистической характеристикой этого слагаемого является его дисперсия, так как его среднее равно нулю, а закон распределения не имеет значения, ввиду того, что для моделируемого процесса плотность вероятности не задается. Эта дисперсия может быть определена исходя из того, что второе слагаемое в (2.87) равно результату действия белого шума со спектральной плотность мощности на линейную цепь с импульсной характеристикой равной на интервале :

(2.89)

Подставив (2.88) в (2.87) и учтя, что дисперсия второго слагаемого должна быть равна (2.89) и , получим , где нормированная (с единичной дисперсией) случайная величина с нулевым средним. Таким образом, значение моделируемого случайного процесса в момент времени выражается через значение простым соотношением, которое позволяет записать рекуррентное выражение для последовательности дискретных отсчетов:.

(2.90)

Дисперсия независимых случайных величин с нулевым средним равна единице.

Это выражение соответствует рекурсивному фильтру первого порядка с передаточной функцией

(2.91)

Этот фильтр обеспечивает формирование случайного процесса в схеме (см. рис. 2.2) с корреляционной функцией, совпадающей с заданной корреляционной функцией в дискретные моменты времени, т.е. нулевую методическую погрешность по корреляционной функции. Напомним, что методическая погрешность по спектральной плотности мощности в этом случае не равна нулю, т.е. заданная спектральная плотность мощности и спектральная плотность мощности процесса не совпадают. В самом деле, передаточная функция по частоте синтезированного цифрового формирующего фильтра (2.91) равна

В соответствии с этим спектральная плотность мощности процесса , формируемого этим фильтром из дискретного белого шума (см. рис. 2.3.) с дисперсией , равна 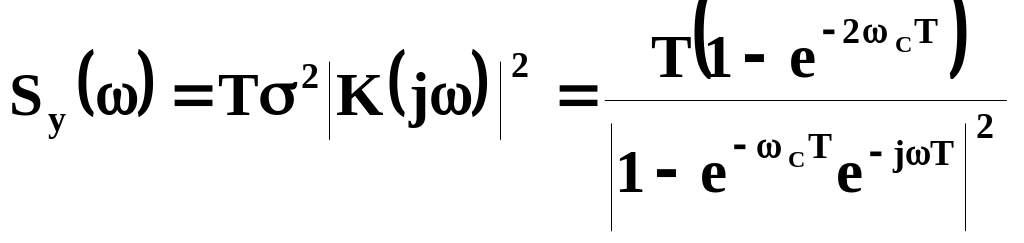, что не совпадает с заданной спектральной плотностью мощности .

Подход, рассмотренный в этом примере, позволяет синтезировать цифровые рекурсивные формирующие фильтры с нулевой методической погрешностью по заданной корреляционной функции. При этом, естественно, предполагается, что дробнорациональная спектральная плотность мощности может быть факторизована таким образом, чтобы ей соответствовал аналоговый формирующий фильтр на элементах с сосредоточенными параметрами.

Метод синтеза цифрового рекурсивного формирующего фильтра с нулевой погрешностью по корреляционной функции допускает обобщение на случай, когда шаг дискретизации является непостоянным, т.е. позволяет производить цифровое моделирование стационарных процессов с заданной корреляционной функцией в неравноотстоящих точках. В самом деле, выражение (2.90) в соответствии с (2.87), (2.88), (2.89) может быть записано как , где переменный шаг дискретизации, зависящий от номера такта моделирования, .

2.2.4. СРАВНЕНИЕ МЕТОДОВ МОДЕЛИРОВАНИЯ СТАЦИОНАРНЫХ СЛУЧАЙНЫХ ПРОЦЕССОВ С ЗАДАННЫМИ КОРРЕЛЯЦИОННЫМИ СВОЙСТВАМИ

Рассмотренные методы моделирования стационарных случайных процессов с заданными корреляционными свойствами различаются как сложностью подготовительной работы, так и свойствами алгоритмов моделирования.

Метод канонических и неканонических разложений целесообразно применять, в тех случаях, когда необходимо моделировать стационарный случайный процесс в произвольные, заранее неопределенные моменты времени. Если моменты времени, в которых необходимо имитировать случайный процесс, определены заранее, применение методов канонических разложений нецелесообразно из-за присущих им недостатков. Метод неканонического разложения выгоднее метода канонических разложений в смысле экономии памяти и машинного времени, но он может быть использован, когда его недостаток, проявляющийся в неэргодичности процесса, не имеет принципиального значения.

Метод формирующего фильтра получил наибольшее распространение, так как позволяет экономить машинные ресурсы и имитировать реализации с любой длительностью, заранее неопределенной. При этом применение нерекурсивных фильтров более универсально, так как позволяет синтезировать формирующие фильтры для любых типов корреляционных функций и спектральных плотностей.

Применение рекурсивных фильтров по сравнению с нерекурсивными позволяет более экономно расходовать машинные ресурсы. Поэтому, когда это возможно, т.е. когда заданная спектральная плотность мощности является дробно-рациональной функцией, необходимо использовать рекурсивные формирующие фильтры, применяя факторизацию спектральной плотности мощности.

Если заданная спектральная плотность мощности не является дробно-рациональной функцией, необходимо использовать методы синтеза нерекурсивных фильтров с помощью решения системы нелинейных уравнений или разложения спектральной плотности мощности в ряд Фурье.

Применение нерекурсивных формирующих фильтров практически всегда приводит к методической погрешности, которая, однако, может быть уменьшена до требуемого уровня за счет уменьшения шага дискретизации и (или) увеличения длительности импульсной характеристики формирующего фильтра. Таким образом, величина методической погрешности ограничена лишь имеющимися при моделировании ресурсами  объемом памяти и быстродействием используемого компьютера.

Если заданная спектральная плотность мощности является дробно-рациональной и используется рекурсивный формирующий фильтр, то предварительно должна быть найдена передаточная функция аналогового формирующего фильтра путем факторизации спектральной плотности мощности. Если найденная передаточная функция аналогового формирующего фильтра имеет число нулей больше, чем число полюсов, для синтеза цифрового формирующего фильтра целесообразно применять метод согласованного -преобразования. В случае, когда число нулей менее или равно числу полюсов передаточной функции, целесообразно использовать метод билинейного -преобразования, обеспечивающий в определенном диапазоне частот совпадение заданной и реализуемой спектральной плотности мощности. Когда число нулей передаточной функции аналогового формирующего фильтра меньше, чем число ее полюсов, целесообразно также использование метода, обеспечивающего нулевую методическую погрешность по корреляционной функции.

Следует учитывать общий недостаток методов формирующего фильтра - возможность появления на начальных тактах моделирования отсчетов процесса, не соответствующих заданным статистическим свойствам. Чтобы исключить этот интервал моделирования, необходимо, чтобы переходной процесс, связанный с установлением требуемых статистических свойств моделируемого процесса, закончился. Обычно для этого достаточно интервала времени, равного длительности импульсной характеристики нерекурсивного формирующего фильтра, или двухтрёх интервалов корреляции моделируемого случайного процесса.

Если моделируется нормальный процесс, то целесообразно использование датчиков случайных чисел с нормальным законом распределения. Если одномерная плотность не задана, обычно применяется датчик с равномерным распределением.