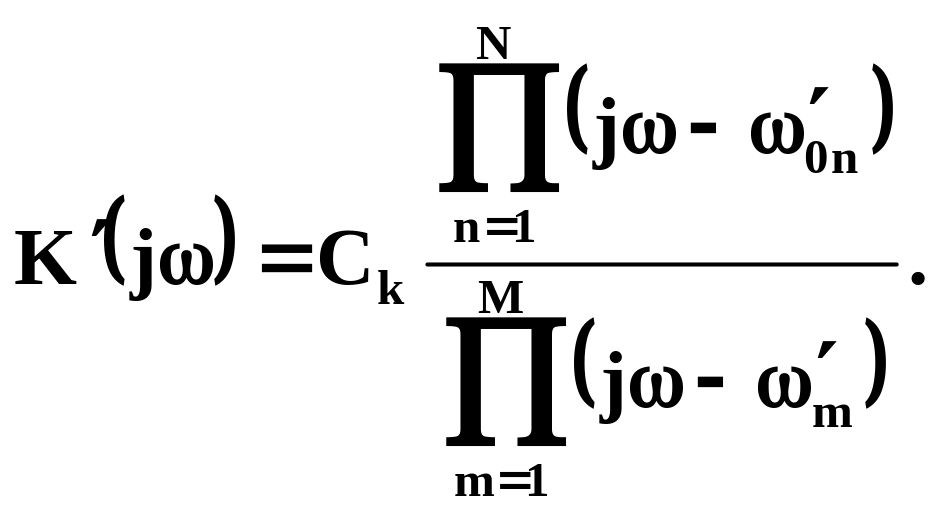Рекурсивный формирующий фильтр

Применение рекурсивных формирующих фильтров позволяет существенно экономить машинные ресурсы по сравнению с использованием нерекурсивных фильтров. Однако применение рекурсивных фильтров оказывается возможным, когда заданная спектральная плотность мощности является дробнорациональной функцией. Еще одно достоинство применения рекурсивных формирующих фильтров  возможность обеспечения нулевой методической (алгоритмической) погрешности.

Синтез рекурсивного формирующего фильтра по аналоговому формирующему фильтру

Рассмотрим синтез цифрового рекурсивного формирующего фильтра на основе построения дискретного аналога для аналогового формирующего фильтра.

Очевидно, что первым шагом является нахождение аналогового формирующего фильтра.

Нахождение аналогового формирующего фильтра по заданной дробно-рациональной спектральной плотности мощности было рассмотрено выше. В результате такого синтеза определялась передаточная функция аналогового формирующего фильтра (2.77)

(2.84)

Передаточная функция аналогового формирующего фильтра (2.84) является дробнорациональной функцией переменной. Метод перехода от аналогового формирующего фильтра к цифровому может быть выбран из различных соображений в зависимости от технического задания на моделирование[5].

Наиболее распространенными методами построения цифровой модели аналогового фильтра являются методы инвариантности импульсной характеристики и билинейного -преобразования [1, 5]. Применение метода инвариантности импульсной характеристики уже рассматривалось при синтезе нерекурсивного формирующего фильтра. Применение метода приводило к методической погрешности (см. разд. 2.2.3) как в отношении корреляционной функции, так и в отношении спектральной плотности мощности. Однако уменьшение шага дискретизации позволяет уменьшить методическую погрешность до любой заданной величины.

Более целесообразным может оказаться применение метода билинейного -преобразования, называемого еще методом инвариантности частотных характеристик. Метод обеспечивает совпадение передаточных функций аналогового и цифрового фильтров на частотах . Так как частотные характеристики аналогового и цифрового формирующего фильтров при этом условии совпадают, то в соответствии с (2.42) в указанном диапазоне частот будет обеспечиваться практическое совпадение заданной спектральной плотности мощности и спектральной плотности мощности формируемого дискретного случайного процесса (см. рис. 2.3). Метод билинейного -преобразования заключается в переходе от передаточной функции аналогового фильтра (2.84) к передаточной функции цифрового фильтра путем подстановки , т.е. передаточная функция цифрового формирующего фильтра при этом методе определяется как

(2.85а)

где определяется как (2.84).

После несложных алгебраических преобразований от передаточной функции , полученной в соответствии с этим выражением, можно перейти к стандартной форме записи передаточной функции (2.38) и к реализации цифрового формирующего фильтра по формуле (2.36) или по схеме рис. 2.5.

Пример 2.7.

Осуществить моделирование стационарного процесса с корреляционной функцией , применяя рекурсивный формирующий фильтр.

Как показано в примере 2.5, передаточная функция аналогового формирующего фильтра, полученная на основе факторизации спектральной плотности мощности, есть

Применим метод билинейного преобразования для получения передаточной функции рекурсивного формирующего фильтра. В соответствии с (2.85) передаточная функция цифрового формирующего фильтра равна

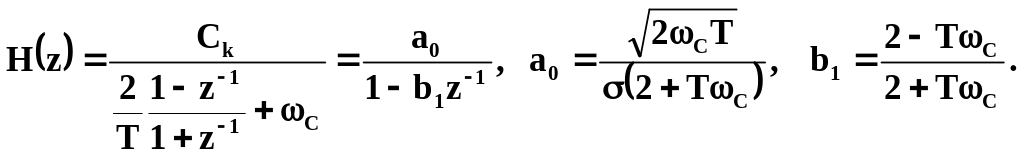
В соответствии с (2.36) формула вычислений для синтезированного рекурсивного фильтра есть .

Схема вычислений в соответствии с рис. 2.5 приведена на рис. 2.21.

С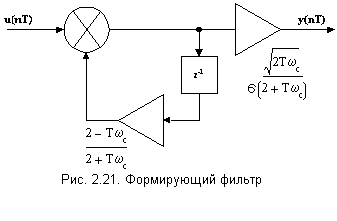 овпадение заданной спектральной плотности мощности со спектральной плотностью мощности моделируемого случайного процесса не обеспечивает отсутствие методической погрешности по заданной корреляционной функции из-за замены случайного процесса, описываемого как функция непрерывного времени на дискретный случайный процесс . Разработаны специальные методы перехода от аналогового формирующего фильтра к цифровому, обеспечивающие нулевую методическую погрешность по автокорреляционной функции [1, 2] и рассмотренные в следующем параграфе.

Метод билинейного преобразования не может быть использован, когда в передаточной функции (2.84) синтезированного аналогового фильтра число нулей превышает число полюсов [5]. В этом случае можно применить метод согласованного преобразования для синтеза цифрового фильтра по (2.84). Метод заключается в том, что передаточная функция цифрового формирующего фильтра записывается по (2.84) как

(2.85б)

Пример 2.8.

П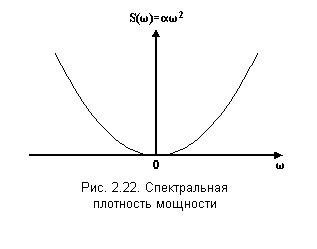 усть необходимо осуществить моделирование случайного процесса со спектральной плотностью мощности (рис. 2.22) .

Синтез аналогового формирующего фильтра произведем, как это было проделано в примере 2.5.

1. Спектральная плотность мощности имеет два нуля и не имеет полюсов (2.71). Нули спектральной плотности мощности равны .

2. Из двух нулей для синтезирования передаточной функции аналогового формирующего фильтра оставляем один.

3. Таким образом, передаточная функция аналогового формирующего фильтра имеет один нуль, равный нулю и не имеет ни одного полюса.

4. В соответствии с (2.77) передаточная функция аналогового формирующего фильтра равна .

Эта передаточная функция соответствует идеальной дифференцирующей цепи, при этом , т.е. метод билинейного преобразования не может быть применен. Применение метода согласованного преобразования (2.85б) дает передаточную функцию цифрового формирующего фильтра (рис. 2.23)

.

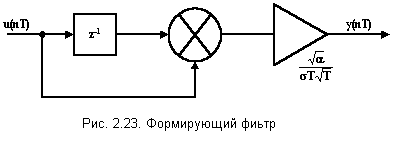
Этот формирующий фильтр является нерекурсивным; в общем случае метод согласованного преобразования приведет к синтезу рекурсивных фильтров.