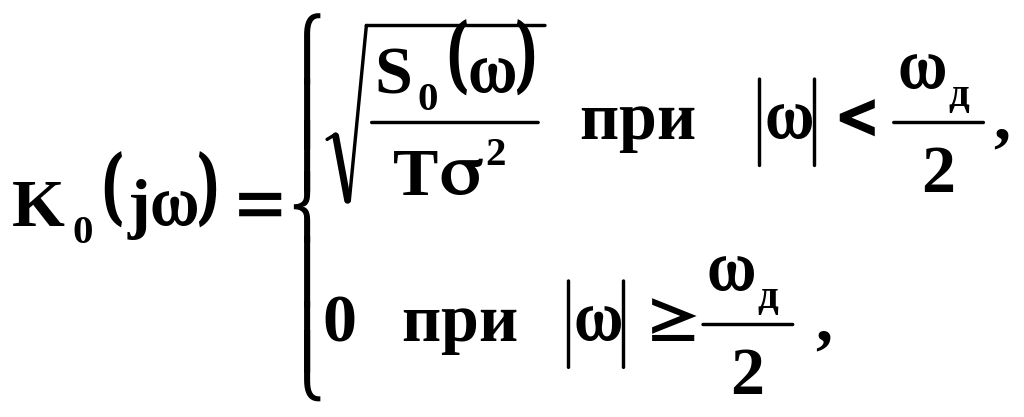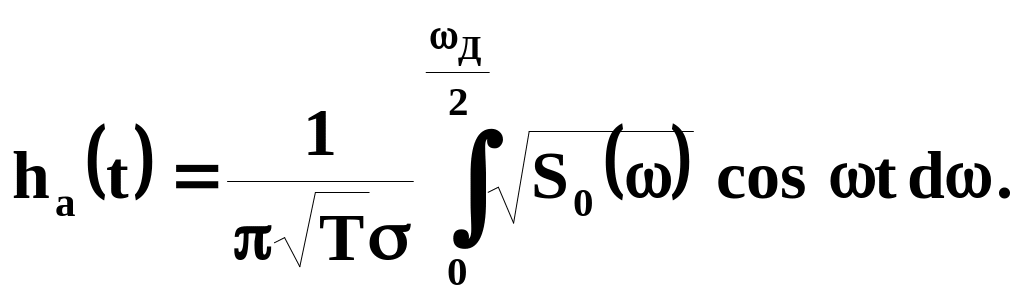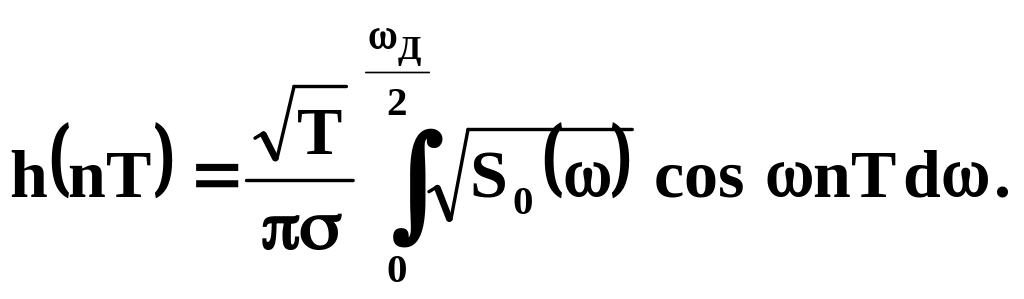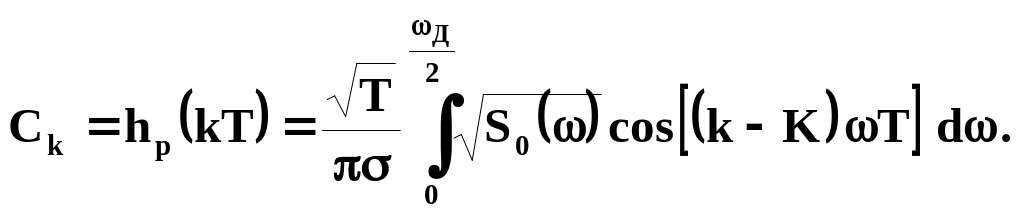Синтез нерекурсивных формирующих фильтров на основе разложения спектральной плотности мощности в ряд фурье

Этот метод позволяет свести определение коэффициентов цифрового формирующего нерекурсивного фильтра к расчету по формулам, что намного удобнее, чем решение системы нелинейных уравнений.

Идея метода заключается в следующем.

При рассматриваемой постановке задачи моделирования известна спектральная плотность мощности процесса.

Коэффициенты нерекурсивного фильтра, как это будет ясно из дальнейшего, определяются как коэффициенты разложения в ряд Фурье передаточной функции формирующего фильтра. Для того чтобы определить коэффициенты Фурье, необходимо, чтобы передаточная функция, а значит, и спектральная плотность мощности были бы равны нулю за пределами частоты дискретизации , связанной с используемым шагом дискретизации как . Поскольку заданная спектральная плотность мощности может отличаться от нуля на частотах, больших , то случайный процесс с заданной спектральной плотностью можно заменить процессом со спектральной плотностью мощности :

(2.54)

Такая замена приводит к методической погрешности при моделировании, однако, обычно спектральная плотность мощности становится малой, начиная с какойто характерной частоты, и шаг дискретизации может быть принят при моделировании достаточно малым, чтобы была больше этой характерной частоты.

По соотношению (2.42) с учетом (2.44) определяются требования к аналоговому формирующему фильтру (см. рис. 2.2) как , где принято .

Таким образом, амплитудно-частотная характеристика аналогового формирующего фильтра должна быть равна

(2.55)

Этому условию может удовлетворять сколь угодно большое количество формирующих фильтров с отличающимися друг от друга фазочастотными характеристиками и, в частности, фильтр с фазочастотной характеристикой, равной нулю. Передаточная функция такого аналогового фильтра в соответствии с (2.55) должна быть равна

(2.56)

а импульсная характеристика определяется как обратное преобразование Фурье от

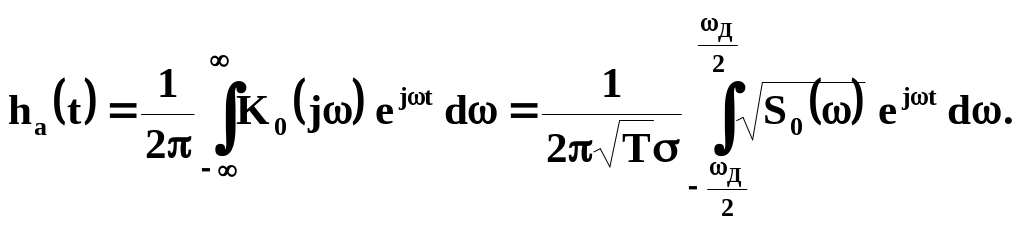
Так как всегда является четной функцией , то

(2.57)

Применим метод инвариантности импульсной характеристики [1, 5] для построения цифрового формирующего фильтра. Импульсная характеристика цифрового фильтра в этом методе связанна с импульсной характеристикой цифрового прототипа как

(2.58)

Таким образом, в соответствии с (2.57) импульсная характеристика цифрового формирующего фильтра должна быть равна

(2.59)

Это выражение соответствует определению коэффициентов ряда Фурье для передаточной функции (2.56) с точностью до множителя (2.55).

Однако непосредственно в виде (2.35) цифровой формирующий фильтр не может быть построен, поскольку он является нереализуемым из-за того, что

(2.60)

Это является следствием того, что четная функция, поэтому в соответствии с (2.59) , а, следовательно, и , что подтверждает (2.60).

Кроме того, и импульсная характеристика аналогового формирующего фильтра , и импульсная характеристика цифрового фильтра в общем случае являются неограниченными во времени функциями. Это препятствует цифровой реализации фильтра в силу конечности памяти и быстродействия реальных компьютеров.

Вместо (2.35), соответствующей формуле вычислений реакции цифрового нерекурсивного фильтра, необходимо выполнять вычисления по формуле

(2.61)

где учтено, что коэффициенты нерекурсивного фильтра равны отсчётам его импульсной характеристики .

Чтобы реализовать нерекурсивный формирующий фильтр, необходимо, чтобы при и длительность , а значит, и число слагаемых в (2.61) были бы конечными.

Чтобы удовлетворить этим условиям, поступают следующим образом (рис. 2.16).

Во-первых, импульсную характеристику (рис. 2.16,а) искусственно ограничивают во времени (рис. 2.16,б):

(2.62)

Практически величину можно выбирать из условия , где полная дисперсия случайного процесса, дисперсия случайного процесса после ограничения (2.62) импульсной характеристики цифрового формирующего фильтра, заданная малая погрешность.

Преобразование (2.62) по-прежнему не обеспечивает возможность реализации цифрового фильтра. Чтобы обеспечить условие реализуемости введем новую импульсную характеристику (рис 2.16,в)

(2.63)

для которой выполняется при .

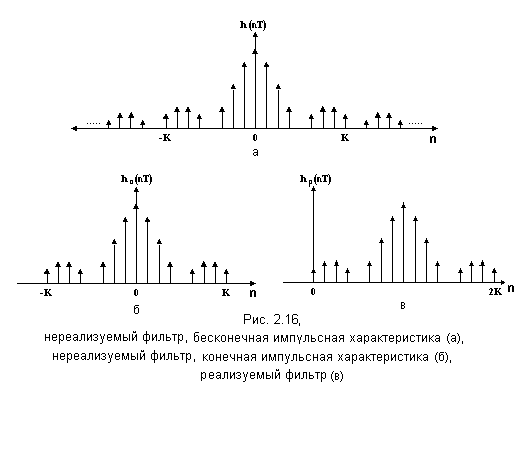
Так как последовательность на входе формирующего фильтра и последовательность на выходе соответствуют стационарным случайным процессам, то сдвиг импульсной характеристики не изменит свойств моделируемого случайного процесса.

Вместо вычислений по формуле (2.61) при формировании случайного процесса будет использоваться соотношение , при этом в соответствии с (2.59), (2.63)

(2.64)

Метод вычисления коэффициентов цифрового формирующего нерекурсивного фильтра как коэффициентов ряда Фурье (2.64) более прост, чем метод определения коэффициентов путем решения системы нелинейных уравнений, который рассмотрен в предыдущем разделе.

Этот метод обладает методической (алгоритмической) погрешностью из-за использования преобразований (2.54) и (2.62). Эта методическая погрешность может быть уменьшена при уменьшении шага дискретизации .

Пример 2.4

П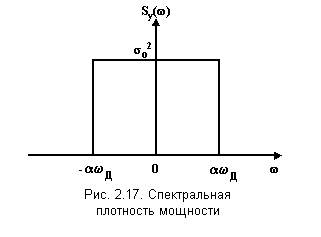 остроим формирующий нерекурсивный фильтр для моделирования случайного процесса со спектральной плотностью мощности (рис. 2.17):

где .

В соответствии с (2.64) определяем импульсную характеристику и коэффициенты формирующего нерекурсивного фильтра:

Пример такой импульсной характеристики представлен на рис. 2.18.