
- •7 Сентября 2000 г.
- •Предисловие
- •1.Моделирование случайных процессов с заданной многомерной плотностью вероятности
- •1.1. Метод условных распределений
- •1.2. Метод неймана (метод отбора)
- •1.3. Моделирование марковских случайных процессов
- •2. Моделирование случайных процессов с заданными корреляционными свойствами
- •2.1. Моделирование нестационарных процессов с заданными корреляционными свойствами
- •2.1.1. Метод линейного преобразования
- •2.1.2. Метод канонических разложений
- •2.1.3. Сравнение методов моделирования нестационарных случайных процессов с заданными корреляционными свойствами
- •2.2. Моделирование стационарных случайных процессов с заданными корреляционными свойствами
- •2.2.1. Метод канонических разложений
- •2.2.2 Метод неканонических разложений
- •2.2.3.Метод формирующего фильтра
- •Нерекурсивный формирующий фильтр (метод скользящего суммирования)
- •Пример 2.3.
- •Синтез нерекурсивных формирующих фильтров на основе разложения спектральной плотности мощности в ряд фурье
- •Синтез нерекурсивных формирующих фильтров на основе факторизации спектральной плотности мощности
- •Рекурсивный формирующий фильтр
- •Синтез рекурсивного формирующего фильтра по аналоговому формирующему фильтру
- •Синтез рекурсивного формирующего фильтра с нулевой методической погрешностью для корреляционной функции
- •2.2.5. Формирующие фильтры для моделирования стационарных случайных процессов с типовыми корреляционными свойствами
- •3.1. Метод неканонических разложений
- •3.2. Метод, основанный на безынерционном нелинейном преобразовании нормального случайного процесса
- •Литература
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
___________________________
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ИНСТИТУТ
(ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)
В.П. БАКАЛОВ
ЦИФРОВОЕ МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ ПРОЦЕССОВ
Учебное пособие
Утверждено
на заседании редсовета
7 Сентября 2000 г.
Москва
Издательство МАИ
2001
621.396.6.(075)
Б 19
УДК: 621.396.6:519.876.5 (075.8)
В.П. Бакалов. Цифровое моделирование случайных процессов: Учебное пособие. – М.: Изд-во МАИ, 2001. – 84 с.: ил.
В пособии рассмотрены методы цифрового моделирования одномерных случайных процессов, заданных в общем виде, с заданными корреляционными свойствами, с одновременно заданными корреляционными свойствами и одномерной плотностью вероятности.
Пособие предназначено для студентов старших курсов факультета "Радиоэлектроника ЛА".
Рецензенты: В.Г. Сергеев, В.В. Сокольский
ISBN 5-7035-2441-5 © Московский государственный авиационный институт
(технический университет), 2001
Предисловие
При автоматизированном проектировании возникает необходимость моделирования случайных процессов. Содержание учебного пособия соответствует разделу курса “Основы компьютерного проектирования и моделирования РЭС”.
Требуемые для работы с пособием теоретические сведения о случайных процессах соответствуют курсу “Радиотехнические цепи и сигналы” [5].
В пособии приводятся методы моделирования случайных процессов с заданной многомерной плотностью вероятности. Такая постановка задачи моделирования случайного процесса имеет важное методическое значение, так как является самой общей, т.е. к ней может быть сведена любая другая задача. В практике моделирования наиболее часто встречается задача моделирования процессов, для которых заданы лишь корреляционные свойства; в соответствии с этим основная часть пособия посвящена моделированию таких процессов, в особенности стационарных. Методы моделирования случайных процессов с заданными корреляционными свойствами являются основой для понимания всего комплекса задач и методов их решения при цифровом моделировании случайных процессов.
В пособии кратко рассмотрено моделирование стационарных процессов с одновременно заданными корреляционными свойствами и одномерной плотностью вероятности.
Цифровое моделирование случайных процессов предполагает использование независимых случайных величин. Способы построения датчиков случайных чисел для генерации таких величин с любыми требуемыми законами распределения рассматриваются в другой части курса “ Основы компьютерного проектирования и моделирования РЭС ”.
1.Моделирование случайных процессов с заданной многомерной плотностью вероятности
Самый общий случай
задания случайного процесса
![]()
задание характеризующей его многомерной
плотности вероятности
задание характеризующей его многомерной
плотности вероятности
В![]() дальнейшем для сокращения записи будем
использовать выражение для многомерной
плотности вероятности в виде
дальнейшем для сокращения записи будем
использовать выражение для многомерной
плотности вероятности в виде
![]() .
Так как моделируемый случайный процесс
является функцией континуального
аргумента, то для полного описания этого
случайного процесса величина
.
Так как моделируемый случайный процесс
является функцией континуального
аргумента, то для полного описания этого
случайного процесса величина
![]() должна была бы быть бесконечно большой,
что невозможно. Практически, чем больше
величина
,
тем более детально статистическое
описание случайного процесса
.
При цифровом моделировании величина
представляет число отсчётов моделируемого
случайного процесса. Так как память
вычислительного устройства ограничена,
то при цифровом моделировании описание
случайного процесса
с помощью многомерной плотности
вероятности
(где
требуемое
при моделировании число отсчётов)
является полным. Фактически при этом
случайный процесс
представляется случайным вектором с
компонентами
должна была бы быть бесконечно большой,
что невозможно. Практически, чем больше
величина
,
тем более детально статистическое
описание случайного процесса
.
При цифровом моделировании величина
представляет число отсчётов моделируемого
случайного процесса. Так как память
вычислительного устройства ограничена,
то при цифровом моделировании описание
случайного процесса
с помощью многомерной плотности
вероятности
(где
требуемое
при моделировании число отсчётов)
является полным. Фактически при этом
случайный процесс
представляется случайным вектором с
компонентами
![]() и моделирование случайного процесса
можно рассматривать как моделирование
совокупности
случайных величин или случайного вектора
с заданной многомерной плотностью
вероятности. На рис. 1.1 представлены
несколько реализаций случайного процесса
;
реализация с номером
и моделирование случайного процесса
можно рассматривать как моделирование
совокупности
случайных величин или случайного вектора
с заданной многомерной плотностью
вероятности. На рис. 1.1 представлены
несколько реализаций случайного процесса
;
реализация с номером
![]() обозначается
обозначается
![]() ,
время моделирования случайного процесса
обозначено
,
время моделирования случайного процесса
обозначено
![]() .
.
На рис. 1.2. показана одна реализация случайного процесса с номером и дискретные отсчеты, которые должны быть определены при цифровом моделировании.
Дискретный отсчет
реализации с номером
для момента времени
![]() обозначается
обозначается
![]() .
Если из контекста ясно, что речь идет о
реализации случайного процесса, то
индекс
может опускаться.
.
Если из контекста ясно, что речь идет о
реализации случайного процесса, то
индекс
может опускаться.
Совместная плотность
вероятности
удовлетворяет условию положительности:
![]() ,
условию
нормировки:
,
условию
нормировки:
|
(1.1) |
условию согласованности:
|
(1.2) |
По плотности вероятности могут быть определены условные плотности вероятности:
|
(1.3) |
п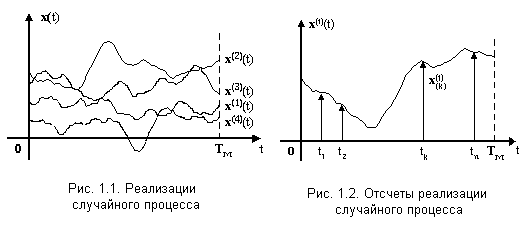 ри
этом числитель и знаменатель (1.3)
определяются в соответствии с (1.2).
ри
этом числитель и знаменатель (1.3)
определяются в соответствии с (1.2).
Цифровое моделирование случайного процесса , заданного с помощью многомерной плотности вероятности , на практике встречается редко. Однако важно, что такое описание случайного процесса является самым полным, и поэтому любой случайный процесс может быть описан таким образом, а значит, если существует метод моделирования при описании случайного процесса с помощью многомерной плотности вероятности , то этот метод может быть использован для моделирования любых случайных процессов. Конечно, такое моделирование не всегда целесообразно, так как для часто встречающихся случайных процессов, например нормальных, разработаны более эффективные в смысле экономии машинных ресурсов методы.
Моделирование случайных процессов должно быть сведено к моделированию случайных независимых величин. Моделирование независимых случайных величин с любыми законами распределения осуществляется с помощью датчиков случайных чисел. Способы построения датчиков случайных чисел рассматриваются в другом курсе.
Известны два метода цифрового моделирования случайных процессов с заданной многомерной плотностью вероятности .
