
- •Математическая статистика теория и практика
- •220301, 230104, 230201 Очной формы обучения
- •Издательство
- •Оглавление
- •§1. Задачи математической статистики
- •§2. Генеральная и выборочная совокупность. Репрезентативность выборки. Способы отбора (способы организации выборки)
- •§3. Статистическое распределение выборки. Графическое представление распределений
- •Эмпирическая функция распределения
- •§4. Статистические оценки параметров распределения
- •§5. Генеральная средняя. Выборочная средняя. Оценка генеральной средней по выборочной средней
- •§6. Генеральная дисперсия. Выборочная дисперсия. Оценка генеральной дисперсии по исправленной дисперсии
- •§7. Метод моментов и метод наибольшего правдоподобия нахождения оценок параметров. Метод моментов
- •Метод наибольшего правдоподобия
- •§8. Доверительная вероятность. Доверительный интервал
- •Доверительный интервал для оценки математического ожидания
- •§9. Проверка гипотезы о соответствии статистических данных теоретическому закону распределения
- •§ 10. Понятие о корреляционном и регрессивном анализе
- •Индивидуальные задания
- •Ответы и указания
- •Приложения
- •Алгоритм проверки гипотез о законе распределения случайных величин
- •О нормальном законе распределения случайной величины X
- •Критические точки распределения 2
- •Список литературы
- •Учебное издание
- •Математическая статистика теория и практика
§8. Доверительная вероятность. Доверительный интервал
Определение. Интервальной называют оценку, которая определяется двумя числами – концами интервала.
При выборе малого объема точечная оценка значительно отличается от оцениваемого параметра, что приводит к грубым ошибкам. В этом случае применяют интервальную оценку.
Пусть оценка неизвестного параметра θ (θ – постоянное число).
Оценка
![]() тем точнее, чем меньше число δ в неравенстве
тем точнее, чем меньше число δ в неравенстве
![]() .
.
Число δ характеризует точность оценки.
Статистические методы не позволяют категорически подтверждать, что удовлетворяет неравенству , можно лишь говорить о вероятности, с которой осуществимо это неравенство.
Определение. Доверительной вероятностью (надёжностью) оценки по называют вероятность γ, с которой осуществляется неравенство .
Р() = γ. (8)
Обычно в качестве доверительной вероятности γ выбирают γ = 0,9; 0,95; 0,99.
Преобразуем (8):
Р() = γ. (9)
Равенство (9) означает, что с вероятностью γ неизвестное значение параметра попадет в интервал
![]() (10)
(10)
Ранее рассматривали вероятность попадания случайных величин в заданный интервал.
В данном случае величина не случайна ( число, хотя и неизвестное), зато случаен интервал (10), случайно его положение на оси абсцисс, определяемое центром , случайна длина.
Поэтому γ – не вероятность попадания точки в интервале (10), а вероятность того, что случайный интервал (10) накроет точку .




![]()
![]()
Определение. Доверительным называют интервал , который накрывает параметр с заданной доверительной вероятностью γ.
Доверительный интервал для оценки математического ожидания
нормального распределения при известном σ
(σ – среднее квадратное отклонение)
Дано: Количественный параметр Х генеральной совокупности распределен нормально.
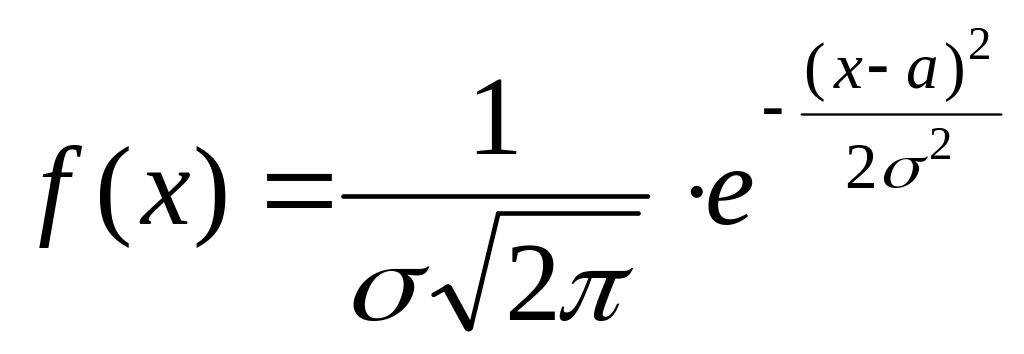 плотность.
плотность.
Математическое ожидание a – неизвестно.
Среднее
квадратическое отклонение
![]() – известно.
– известно.
Требуется:
оценить а
по средней выборочной
![]() .
.
Данные
выборки и среднее выборочное будем
рассматривать как случайные величины
![]() и
,
одинаково распределённые с математическим
ожиданием a
и средним квадратическим отклонением
.
и
,
одинаково распределённые с математическим
ожиданием a
и средним квадратическим отклонением
.
![]() ,
,
![]() ;
;
![]() .
.
Пусть
выполняется Р(![]() )=
γ,
где γ
– заданная вероятность.
)=
γ,
где γ
– заданная вероятность.
Из
курса теории вероятностей известна
формула: Р(
)
=
![]() .
Заменим X
на
.
Заменим X
на
![]() ,
на
,
на
![]() .
.
Р(
)
=
![]() =
=
![]() ,
где
,
где
![]() .
.
Тогда
![]() .
Следовательно, Р(
.
Следовательно, Р(![]() )=
.
)=
.
Вернемся к обозначению
![]() как
.
Получим
как
.
Получим
Р(![]() .
.
Итак,
с достоверной вероятностью γ
можно утверждать, что доверительный
интервал
![]() покрывает неизвестный параметр a.
Точность
оценки
.
Число
t
определяется из равенства
покрывает неизвестный параметр a.
Точность
оценки
.
Число
t
определяется из равенства
![]() ,
или
,
или
![]() .
.
При
заданной доверительной вероятности
![]() по таблице функции Лапласа (табл. 2)
находят значение t.
по таблице функции Лапласа (табл. 2)
находят значение t.
Пример
10.
Количественный
параметр X
распределен нормально,
![]() .
Найти доверительный интервал для оценки
неизвестного математического ожидания
a
по выборочной средней
,
если объем выборки n
=
36 и доверительная вероятность
= 0,95.
.
Найти доверительный интервал для оценки
неизвестного математического ожидания
a
по выборочной средней
,
если объем выборки n
=
36 и доверительная вероятность
= 0,95.
Решение.
;
![]() .
.
![]()
![]() –
доверительный
интервал.
–
доверительный
интервал.
Если,
например,
![]() ,
то (3,12; 5,08).
,
то (3,12; 5,08).
Смысл результата: если произведено достаточно большое число выборок, то 95% из них определяют такие доверительные интервалы, в которых неизвестное математическое ожидание а действительно заключено. Лишь в 5% случаев а может выйти за границы доверительного интервала.
Вычисление
объема выборки при заданных
![]() и
и
Пусть требуется оценить математическое ожидание, если заданы доверительная вероятность и точность оценки .
Точность
оценки
.
Тогда
![]() .
.
Значит,
![]() –
минимальный объем выборки, который
обеспечит заданную точность
.
–
минимальный объем выборки, который
обеспечит заданную точность
.
Замечание. Доверительный интервал для оценки математического ожидания нормального распределения при неизвестном .
X – количественный признак, распределён нормально. a, – неизвестны.
Требуется оценить a .
Можно
доказать, что
![]()
доверительный интервал, покрывающий
неизвестное математическое ожидание
a
с доверительной вероятностью
,
где – выборочная средняя;
доверительный интервал, покрывающий
неизвестное математическое ожидание
a
с доверительной вероятностью
,
где – выборочная средняя;
![]() – исправленное среднее квадратическое
отклонение;
– исправленное среднее квадратическое
отклонение;
![]() – квантиль распределения, который
находят по таблице 3 по заданным
– квантиль распределения, который
находят по таблице 3 по заданным
![]() и
.
и
.
Задачи _______________________________________________________
Найти доверительный интервал для оценки с надежностью 0,99 неизвестного математического ожидания a нормально распределённого признака Х генеральной совокупности, если известны генеральное среднее квадратичное отклонение σ = 4, выборочная средняя
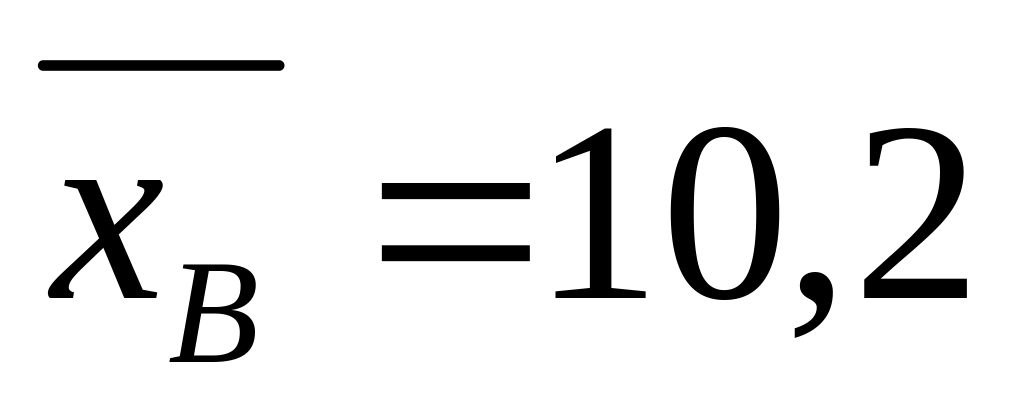 и объём выборки n = 16.
и объём выборки n = 16.На овцеводческой ферме из стада произведена выборка для взвешивания 36 овец. Их средний вес оказался равным 50 кг. Предположив распределение веса нормальным и определив несмещённую оценку выборочной дисперсии S2 = 16, найти доверительный интервал для оценки математического ожидания с надёжностью 0,95.
Выборка из большой партии электроламп содержит 100 ламп. Средняя продолжительность горения лампы выборки оказалась равной 1000 ч. Найти с надежностью 0,95 доверительный интервал для средней продолжительности a горения лампы всей партии, если известно, что продолжительность горения лампы распределена нормально.
Найти минимальный объём выборки, при котором с надежностью 0,975 точность оценки математического ожидания a генеральной совокупности по выборочной средней равна δ = 0,3, если известно среднее квадратичное отклонение σ = 1,2 нормально распределённой генеральной совокупности.
Найти минимальный объем выборки, при котором с надежностью 0,925 точность оценки математического ожидания нормально распределённой генеральной совокупности по выборочной средней равна 0,2, если известно среднее квадратичное отклонение генеральной совокупности σ = 1,5.
Из генеральной совокупности извлечена выборка:
xi |
-2 |
1 |
2 |
3 |
4 |
5 |
ni |
2 |
1 |
2 |
2 |
2 |
1 |
Оценить с надежностью 0,95 математическое ожидание a нормально распределённого признака генеральной совокупности по выборочной средней при помощи доверительного интервала.
Из генеральной совокупности извлечена выборка:
xi |
-0,5 |
-0,4 |
-0,2 |
0 |
0,2 |
0,6 |
0,8 |
1 |
1,2 |
1,5 |
ni |
1 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
1 |
Оценить с надежностью 0,95 математическое ожидание a нормально распределённого признака генеральной совокупности по выборочной средней при помощи доверительного интервала.
По данным выборки объёма n = 50 из генеральной совокупности нормально распределённого количественного признака найдено исправленное среднее квадратичное отклонение s = 14. Найти доверительный интервал, покрывающий генеральное среднее квадратичное отклонение σ с надежностью 0,999.
Случайная величина Х распределена по нормальному закону. Статистическое распределение выборки представлено в таблице:
xi |
3 |
5 |
7 |
8 |
10 |
12 |
14 |
ni |
3 |
7 |
4 |
6 |
7 |
5 |
8 |
Найти с надежностью 0,97 доверительный интервал для оценки математического ожидания и с надежностью 0,95 – для оценки среднего квадратичного отклонения.
Случайная величина Х распределена по нормальному закону. Статистическое распределение выборки представлено в таблице:
xi |
1 |
3 |
5 |
7 |
9 |
ni |
2 |
5 |
4 |
6 |
3 |
Найти с надежностью 0,95 доверительный интервал для оценки математического ожидания и с надежностью 0,99 – для оценки среднего квадратичного отклонения.
