
- •Математическая статистика теория и практика
- •220301, 230104, 230201 Очной формы обучения
- •Издательство
- •Оглавление
- •§1. Задачи математической статистики
- •§2. Генеральная и выборочная совокупность. Репрезентативность выборки. Способы отбора (способы организации выборки)
- •§3. Статистическое распределение выборки. Графическое представление распределений
- •Эмпирическая функция распределения
- •§4. Статистические оценки параметров распределения
- •§5. Генеральная средняя. Выборочная средняя. Оценка генеральной средней по выборочной средней
- •§6. Генеральная дисперсия. Выборочная дисперсия. Оценка генеральной дисперсии по исправленной дисперсии
- •§7. Метод моментов и метод наибольшего правдоподобия нахождения оценок параметров. Метод моментов
- •Метод наибольшего правдоподобия
- •§8. Доверительная вероятность. Доверительный интервал
- •Доверительный интервал для оценки математического ожидания
- •§9. Проверка гипотезы о соответствии статистических данных теоретическому закону распределения
- •§ 10. Понятие о корреляционном и регрессивном анализе
- •Индивидуальные задания
- •Ответы и указания
- •Приложения
- •Алгоритм проверки гипотез о законе распределения случайных величин
- •О нормальном законе распределения случайной величины X
- •Критические точки распределения 2
- •Список литературы
- •Учебное издание
- •Математическая статистика теория и практика
§6. Генеральная дисперсия. Выборочная дисперсия. Оценка генеральной дисперсии по исправленной дисперсии
Определение.
Генеральной дисперсией
DГ
называют среднее арифметическое
квадратов отклонения значений признака
Х
генеральной совокупности от его среднего
значения
![]() .
.
Если
различны, то
 ,
где N
– объём выборки.
,
где N
– объём выборки.
Если
имеют частоты , то
 .
.
Определение.
Генеральным средним квадратическим
отклонением
называют
![]() .
.
Определение.
Выборочной дисперсией
![]() называют среднее арифметическое
квадратов отклонения наблюдаемых
значений признака от их среднего значения
.
называют среднее арифметическое
квадратов отклонения наблюдаемых
значений признака от их среднего значения
.
Если
различны, то
 .
.
Если
имеют частоты , то
 .
.
Замечание. При решении практических задач выборочную дисперсию удобнее находить по следующей формуле:
![]()
(3)
Определение.
Выборочным средним квадратичным
отклонением
называют
![]() .
.
Задача. По данным выборки найти оценку для неизвестной DГ.
Если в качестве оценки для DГ взять DВ, то эта оценка является смещённой, а именно
![]() (без доказательства).
(4)
(без доказательства).
(4)
Значит, эта оценка будет приводить к систематическим ошибкам (давая заниженное значение генеральной дисперсии).
Для
получения несмещенной оценки исправим
выборочную дисперсию, умножив её на
![]() .
.
Определение. Исправленной (эмпирической) дисперсией называется
![]() .
(5)
.
(5)
Значит,
 ,
или
,
или
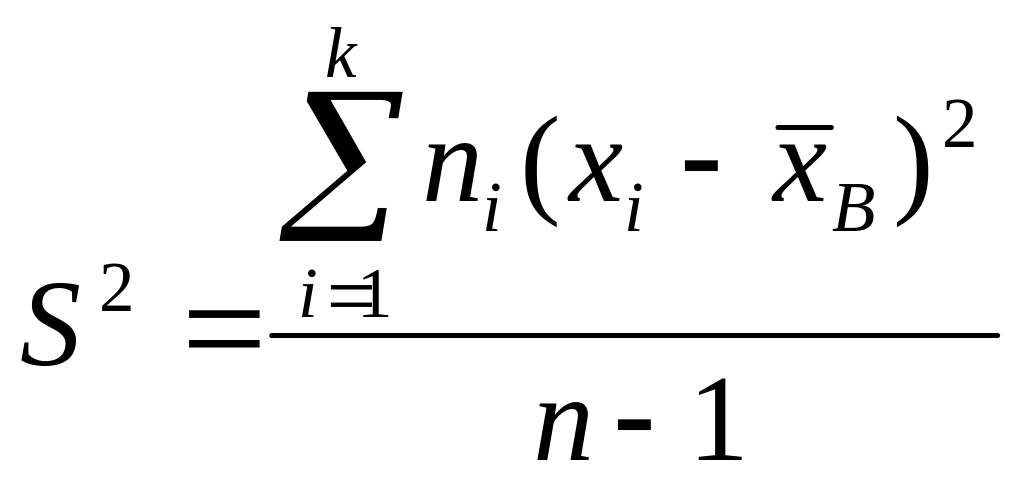 ,
,
где
![]() – несмещённая оценка генеральной
дисперсии DГ.
– несмещённая оценка генеральной
дисперсии DГ.
Действительно,
![]()
Можно
доказать, что
![]() – состоятельная оценка DГ,
а значит также состоятельная
оценка
DГ
(т.к. множитель
– состоятельная оценка DГ,
а значит также состоятельная
оценка
DГ
(т.к. множитель
![]() при
при
![]() ).
).
Замечание. При больших значениях n обе оценки и различаются мало и введение поправочного коэффициента теряет смысл.
Для
оценки среднего квадратического
отклонения генеральной совокупности
используют исправленное среднее
квадратическое отклонение
![]() .
не
является несмещённой
оценкой Г.
.
не
является несмещённой
оценкой Г.
Определение. Точечной называют оценку, которая определяется одним числом.
Рассмотренные оценки являются точечными.
Пример 9. Выборка задана следующим ДCР. Найти смещённую и исправленную оценку для дисперсии.
xi |
-2 |
-1 |
0 |
1 |
2 |
ni |
10 |
20 |
40 |
20 |
10 |
Решение. Предварительно найдем для каждой варианты соответствующую относительную частоту и результаты внесем в таблицу. Объём выборки n = 100.
xi |
-2 |
-1 |
0 |
1 |
2 |
ni |
10 |
20 |
40 |
20 |
10 |
wi |
0,1 |
0,2 |
0,4 |
0,2 |
0,1 |
Найдем смещённую
оценку генеральной дисперсии –
воспользуемся формулой (3):
![]() .
.
Выборочную среднюю
![]() найдем по формуле (2):
найдем по формуле (2):
![]() .
Отсюда,
.
Отсюда,
![]() .
.
Несмещённую оценку
генеральной дисперсии найдем по формуле
(5):
![]() .
.
Задачи _______________________________________________________
Из генеральной совокупности извлечена выборка. Найти несмещённую оценку генеральной средней.
xi
2
5
7
10
ni
16
12
8
14
Из генеральной совокупности извлечена выборка. Найти несмещенную оценку генеральной средней.
xi
1
3
6
26
ni
8
40
10
2
Найти выборочную среднюю по данному распределению выборки:
xi
2560
2600
2620
2650
2700
ni
2
3
10
4
1
Найти выборочную дисперсию по данному распределению выборки:
xi
340
360
375
380
ni
20
50
18
12
Найти выборочную дисперсию по данному распределению выборки:
xi
0,01
0,04
0,08
ni
5
3
2
Найти выборочную дисперсию по данному распределению выборки:
xi
0,1
0,5
0,6
0,8
ni
5
15
20
10
Найти выборочную дисперсию по данному распределению выборки:
xi
18,4
18,9
19,3
19,6
ni
5
10
20
5
Найти исправленную выборочную дисперсию по данному распределению выборки:
xi
102
104
108
ni
2
3
5
Найти исправленную выборочную дисперсию по данному распределению выборки:
xi
0,1
0,5
0,7
0,9
ni
6
12
1
1
Найти исправленную выборочную дисперсию по данному распределению выборки:
xi |
23,5 |
26,1 |
28,2 |
30,4 |
ni |
2 |
3 |
4 |
1 |
