§9. Проверка гипотезы о соответствии статистических данных теоретическому закону распределения

Предположение о том, что статистические данные о количественном признаке Х соответствуют теоретическому закону распределения (назовём его А), является статистической гипотезой, обозначаемой чаще всего через Н . Ставится задача – проанализировав экспериментально полученные данные, обосновать выбор одного из двух решений:

1) принять гипотезу о распределении статистических данных по закону А;

2) отвергнуть гипотезу о соответствии данных выборки закону распределения А.

В силу того, что данные выборки случайны, нет гарантии, что принятое решение будет правильным. Возможны два варианта ошибок:

1) ошибка 1-го рода – отвергнута правильная гипотеза;

2) ошибка 2-го рода – принята неправильная гипотеза.

Всю ситуацию можно описать таблицей 4

Таблица 4

Решение	Гипотеза
	правильная	неправильная
Принять гипотезу	Нет ошибки	Ошибка 2-го рода
Отвергнуть гипотезу	Ошибка 1-го рода	Нет ошибки

Вероятность совершить ошибку 1-го рода называют уровнем значимости гипотезы и обозначают . Величину  задают такой, чтобы случайное событие с вероятностью  можно было считать практически невозможным. Обычно используют значения , равные 0,01; 0,05; 0,1. Для проверки статистических гипотез используют специально подобранные случайные величины, оценивающие степень расхождения эмпирического и теоретического законов, называемые критериями. Таким образом, гипотеза Н – есть предположение о характере распределения признака Х, а используемый для проверки критерий называют критерием согласия. Выбор теоретического закона распределения А обычно выполняется по гистограмме интервального статистического ряда на основании соответствия её плотности распределения закону А. Наиболее часто выбирается нормальный закон распределения, и для проверки соответствия ему опытных данных используются критерии согласия Пирсона, Ястремского, Колмогорова, Вилкоксона.

Опишем процедуру проверки гипотезы о соответствии экспериментальных данных нормальному закону распределения по критерию согласия Пирсона.

1. Примем определённое значение уровня значимости .

2. Сгруппируем экспериментальные данные в классы (интервалы) таким образом, чтобы в каждый класс попало не менее пяти наблюдений. Число, полученных классов обозначим k. Для расчёта числа классов без учёта объединения существует несколько формул, например

к  1 + 3,2 lg n, где n – объем выборки.

3. Найдём статические оценки параметров нормального распределения:

a и S _.

4. Найдём для каждого класса (x_i, x_i+1) выровненные частоты =Р_i n, где n – объём выборки; Ф(х) – функция Лапласа:

(11)

5. В качестве критерия согласия рассмотрим случайную величину, обозначаемую ² и определяемую по формуле:

(12)

Случайная величина Пирсона ² имеет специальное распределение, зависящее от числа степеней свободы r. Для гипотезы о нормальном распределении Х, число степеней свободы:

r = k – 3, где k – число классов. (13)

Очевидно, что чем ближе эмпирические частоты n_i к теоретическим (выровненным) частотам , тем более достоверна гипотеза о нормальном распределении, и в то же время тем меньше значение ².

На рисунке 7 изображён график плотности распределения ² (дифференциальной функции f(²)) для r = 6. Вся площадь между графиком и осью абсцисс равна единице. Незаштрихованная часть площади равна вероятности , заштрихованная площадь равна вероятности .

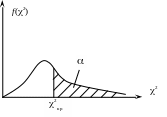
Рис. 7

Пусть заштрихованная площадь равна уровню значимости:

(16)

г де  – вероятность практически невозможного события. Тогда попадание ² в интервал практически невозможно. Заштрихованную площадь называют критической областью данного уровня значимости.

Очевидно, что чем больше , тем меньшим (при данном числе степеней свободы r) будет значение . Имеются таблицы распределения (Пирсона), в которых приведены значения для различного числа степеней свободы r и уровней значимости . При одном и том же уровне значимости  значение возрастает при увеличении числа степеней свободы r.

6. Определяем значение для принятого уровня значимости и числа степеней свободы r.

7. По данным статистического ряда вычисляем наблюдаемое (в данной выборке) значение . Обозначим это значение

(15)

8. Сравнивая и решаем вопрос о принятии или отклонении гипотезы Н о соответствии данных выборки нормальному закону распределения, исходя из следующего:

– если > , то это означает, что наблюдаемое значение попало в критическую область, т.е. произошло событие, которое считали практически невозможным. Следовательно, данные выборки противоречат гипотезе о нормальном распределении, и гипотеза отвергается;

– если , то это означает, что данные выборки не противоречат гипотезе о нормальном распределении, гипотезу можно принять.

Пример 11. Проверка по критерию Пирсона гипотезы о нормальном распределении количественного признака Х по результатам 150 его измерений, сведённых в таблицу частот:

Границы интервала (xi - xi+1)	Частота ni	Относительная частота wi	Середина интервала x*i
24,5–27,5	1	0,0067	26
27,5–30,5	4	0,0267	29
30,5–33,5	13	0,0867	32
33,5–36,5	23	0,1533	35
36,5–39,5	22	0,1467	38
39,5–42,5	29	0,1933	41
42,5–45,5	29	0,1933	44
45,5–48,5	16	0,1067	47
48,5–51,5	11	0,0733	50
51,5–54,5	2	0,0133	53

Построим гистограмму, где по оси абсцисс отложим отрезки [x_i; x_i+1],

а h_i=W_i/x_i=W_i/3.

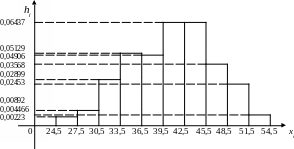
По форме гистограммы выдвинем гипотезу Н : изучаемый признак Х имеет нормальный закон распределения. Найдём оценки числовых характеристик закона:

 выборочные средняя и дисперсия:

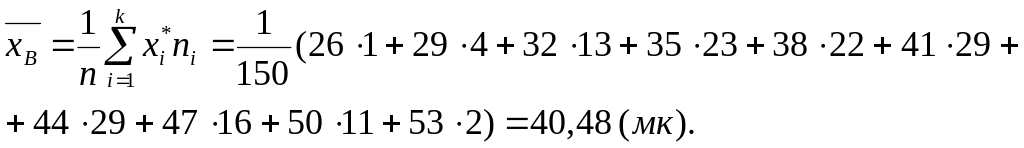
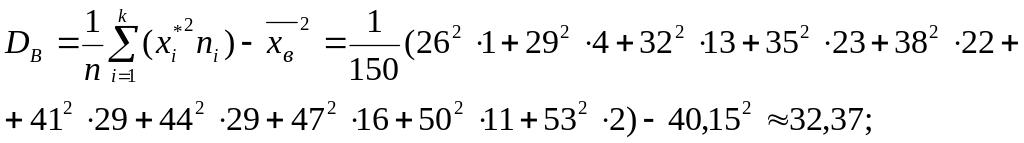
 исправленное среднее квадратичное отклонение:

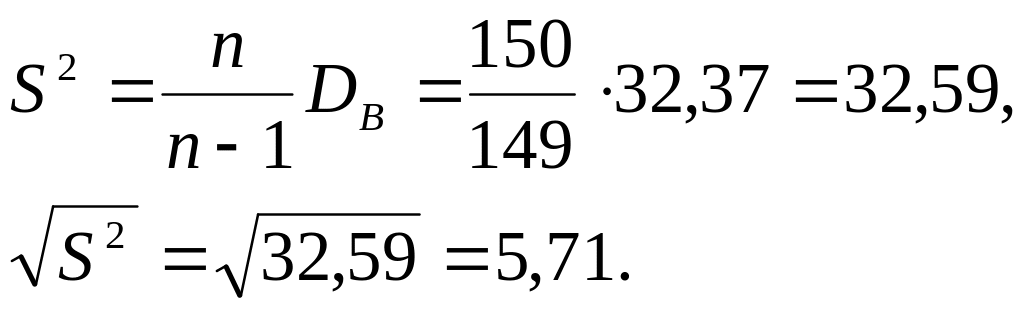
Вычисляем значения аргумента и значения функции Лапласа (по таблице значений функции Лапласа) в этих точках.

Приведём вычисления для первого и последнего классов.

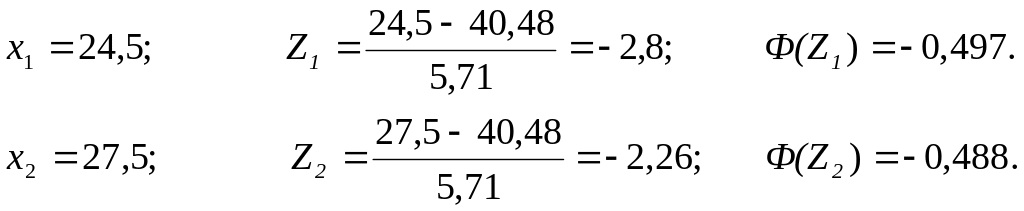
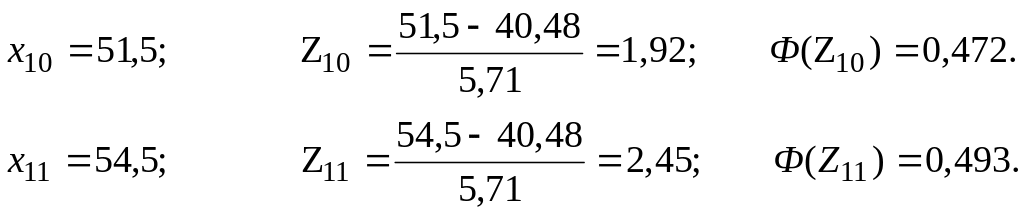
Для остальных классов выравненные относительные частоты P_i и выравненные частоты определяются аналогично.

Выравненные частоты для укрупненных классов приведены в таблице

Границы интервала xi-xi+1	Частота ni	Относительная частота wi	Выравненная относительная частота Pi	Выравненная частота ni'=Pi150
24,5–27,5		0,0067			0,12
27,5–30,5		0,0267
30,5–33,5	13	0,0867	0,0711	10,67	0,51
33,5–39,5	23	0,1533	0,1308	19,62	0,58
36,5–39,5	22	0,1467	0,1905	28,58	1,57
39,5–42,5	29	0,1933	0,2043	30,65	0,09
42,5–45,5	29	0,1933	0,1738	26,07	0,33
45,5–48,5	16	0,1067	0,1086	16,29	0,1
48,5–51,5		0,0733			0,031
51,5–54,5		0,0133

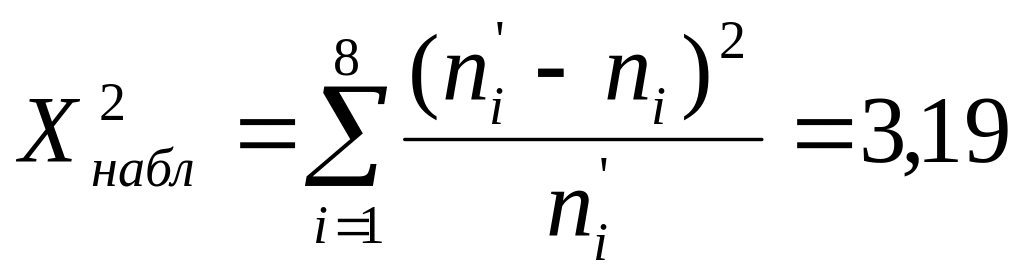
Примечание. Два первых класса и два последних класса объединены ввиду их малочисленности.

Этапы реализации критерия Пирсона:

1. Примем уровень значимости  = 0,05.

2. Сгруппируем классы так, чтобы частота в каждом классе была не менее пяти. Для этого объединим два первых класса и объединим два последних класса. При этом частоты n_i и выравненные частоты n_i’ для объединенных классов суммируются. Число классов стало k = 8. В каждом классе подсчитываем величину .

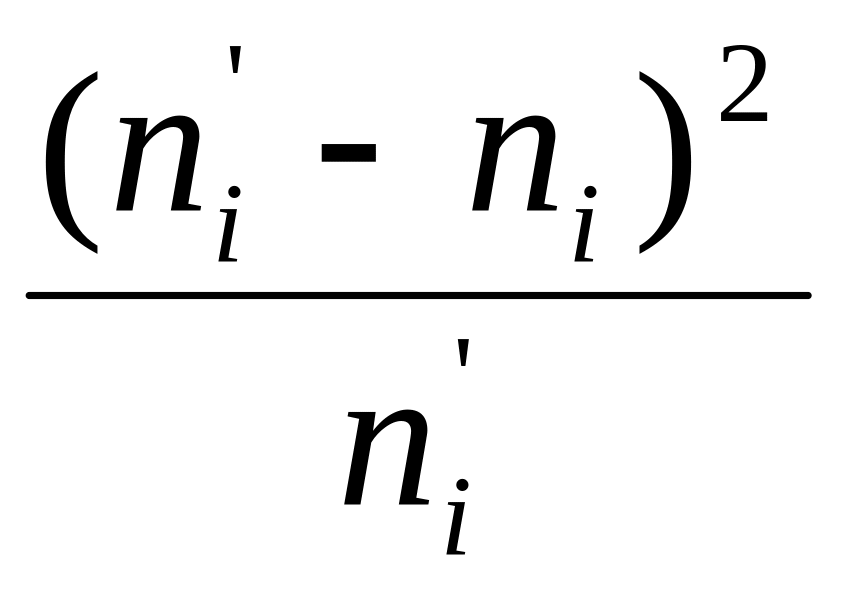3 . Из таблицы критических точек распределения (см. приложение 6) найдем для числа степеней свободы r = 8 – 3 = 5 и принятого уровня значимости  = 0,05. Получим .

4. По последней таблице подсчитываем наблюдаемое значение критерия

5. Сравним и _.

Так как , то гипотезу о нормальном распределении можно считать правдоподобной.

Задачи _______________________________________________________ 

1. Результаты взвешивания 50 случайным образом отобранных пачек чая приведены ниже (в граммах): 150; 147; 152; 148; 149; 153; 151; 150; 149; 147; 153; 151; 152; 151; 149; 152; 150; 148; 152; 150; 152; 151; 148; 151; 152; 150; 151; 149; 148; 149; 150; 150; 151; 149; 151; 150; 151; 150; 149; 148; 147; 153; 147; 152; 150; 151; 149; 150; 151; 153. Можно ли утверждать при уровне значимости α = 0,05, что случайная величина X – масса пачки чая – подчинена нормальному закону распределения?

2. Масса (в граммах) произвольно выбранных 30 пачек полуфабриката «Геркулес» такова: 503; 509; 495; 493; 489; 485; 507; 511; 487; 495; 506; 504; 507; 511; 499; 491; 494; 518; 506; 515; 487; 509; 507; 488; 495; 490; 498; 497; 492; 495. Можно ли при уровне значимости α = 0,05 утверждать, что случайная величина X – масса пачки – подчинена нормальному закону распределения?

3. Результаты исследования числа покупателей в универсаме, в зависимости от времени работы, приведены ниже:

Часы работы	[9; 10)	[10; 11)	[11; 12)	[12; 13]
Число покупателей	41	82	117	72

Можно ли утверждать при уровне значимости α = 0,05, что случайная величина X – число покупателей – подчинена нормальному закону распределения?

4. При обследовании диаметров карданных валов автомобиля, выпускаемых заводом, были зафиксированы отклонения от номинала Δd (мкм), приведенные в таблице:

-8,760	-1,455	-1,455	-4,665	-2,250	2,560	-1,645	0,425	0,650	-1,220
-6,280	8,550	3,170	0,360	2,450	1,590	-5,435	4,495	5,140	-6,520
7,655	-2,215	7,045	8,650	-1,660	1-745	-1,460	-4,415	-0,280	3,785
-4,790	1,240	-0,475	-7,440	-1,805	-0,295	-2,695	-0,390	1,145	0,970
2,075	-6,910	0,645	-11,805	-5,435	-5,420	1,590	1,835	-4,960	2,645

Проверить гипотезу о нормальном распределении случайной величины Δd при уровне доверия  = 0,9.

5. Интервал движения поездов метро составляет 2 минуты. В таблице приведены значения случайной величины X – времени ожидания пассажирами поезда:

0,000	0,002	0,007	0,025	0,089	0,312	1,068	1,604	0,014	0,045
1,747	1,677	0,341	0,952	0,945	1,297	1,981	0,214	1,452	0,787
1,954	0,838	0,143	1,317	0,618	1,853	1,555	0,953	1,922	1,653
0,617	0,828	1,413	1,030	1,459	1,483	1,769	1,265	1,669	0,635
0,787	1,004	0,941	0,612	1,200	1,692	1,356	0,908	1,245	1,295

Проверить гипотезу о нормальном распределении случайной величины X при уровне значимости α = 0,01.

6. По данным выборочного обследования получено распределение семей по среднедушевому доходу (в усл. ед.):

10,984	22,672	17,536	21,400	29,096	22,368	25,680	26,040	23,048	17,944
14,952	38,608	30,072	25,576	28,920	27,544	16,304	32,192	33,224	14,568
37,248	21,456	36,272	38,540	22,872	27,792	22,664	17,936	24,552	31,056
17,336	26,984	24,240	13,096	22,112	24,528	20,688	24,376	26,832	26,552
28,320	13,944	26,032	6,112	16,304	16,328	27,936	17,064	27,544	29,232

Проверить гипотезу о нормальном распределении случайной величины – среднедушевого дохода семьи – при уровне доверия  = 0,9.

7. В таблице приведены значения прибыли 50 фирм, принадлежащих одной корпорации, Q (1000 усл. ед.):

4,744	9,127	7,201	8,650	11,536	9,013	10,255	10,390	9,268	7,354
6,232	15,103,	11,902	10,216	11,470	10,954	6,739	12,697	13,084	6,088
14,593	8,671	14,227	15,190	9,202	11,047	9,124	7,351	9,832	12,271
7,126	10,744	9,715	5,536	8,917	9,823	8,383	9,766	10,687	10,582
11,245	5,854	10,387	2,917	6,739	6,748	10,954	11,101	7,024	11,587

Проверить гипотезу о нормальности распределения случайной величины Q при уровне доверия  = 0,99.

8. Имеются данные о годовой мощности М (тыс. т) предприятия цементной промышленности:

11,240	18,545	15,335	17,750	22,560	18,355	20,425	20,650	18,780	15,590
13,720	28,505	23,170	20,360	22,450	21,590	14,565	24,495	25,140	13,400
27,655	17,785	27,045	28,650	18,670	71,745	18,540	15,585	19,720	23,785
15,210	21,240	19,525	12,560	18,195	19,705	17,305	19,610	21,145	20,970
22,075	13,090	20,645	8,195	14,565	14,580	21,590	21,835	15,040	22,645

Проверить гипотезу о нормальности распределения случайной величины М при уровне доверия  = 0,9.

9. Для определения средней заработной платы работников определённой отрасли было обследовано 100 человек. Результаты представлены в следующей таблице (данные условные):

Зарплата, долл.	[190; 192)	[192; 194)	[194; 196)	[196; 198)	[198; 200)
Число человек	1	5	9	22	28
Зарплата, долл.	[200; 202)	[202; 204)	[204; 206)	[206; 208]
Число человек	19	11	4	1

Выяснить, можно ли при уровне значимости α = 0,05 считать нормальным распределение средней заработной платы.

10. В 1889–1890 годах был измерено рост 1000 взрослых мужчин (рабочих московских фабрик). Результаты измерений представлены в таблице:

Рост, см	[143; 146)	[146; 149)	[149; 152)	[152; 155)	[155; 158)
Число человек	1	2	8	26	65
Рост, см	[158; 161)	[161; 164)	[164; 167)	[167; 170)	[170; 173)
Число человек	120	180	201	170	120
Рост, см	[173; 176)	[176; 179)	[179; 182)	[182; 185)	[185; 188]
Число человек	64	28	10	3	1

Проверить при уровне доверия 0,95 гипотезу, состоящую в том, что рост взрослого мужчины (случайная величина Х) имеет нормальное распределение.