
- •1 Опытом или испытанием будем называть всякое осуществление определённого комплекса условий или действий, при которых происходит данное явление.
- •Свойства классической вероятности:
- •3 Статистическое определение вероятности.
- •7 Формула полной вероятности.
- •15 Предельные теоремы Лапласа и Пуассона. Геометрические вероятности
- •12 Схема независимых испытаний Бернулли
- •Распределённых по закону Пуассона
- •23 Теорема (збч в форме Чебышова)
7 Формула полной вероятности.
Предположим,
что событие А происходит одновременно
с одним из событий H1,
H2,…,Hn,
попарно несовместных и образующих
полную группу событий.Т.к. заранее
неизвестно, с каким из событий Hi
событие А произойдет,
то H1…Hn
– гипотезы. Вероятность
P(A)=P(H1)P(A/H1)+P(H2)P(A/H2)+…+P(Hn)P(A/Hn).Или
P(A)=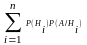
Доказательство:А=AH1+AH2+…+AHn. Т.к. события Hi попарны и несовместны, то будут попарными и несовместными и события AHi. По теореме несовместных событий получаем P(A)=P(AH1+AH2+ …+AHn)= P(H1)+…+P(Hn). P(A)=P(H1)P(A/H1)+P(H2)P(A/H2)+…+P(Hn)P(A/Hn).
Замечание1: Т.к. H1,…,Hn образуют полную вероятность, то сумма вероятностей равна 1: P(H1)+ P(H2)+…+ P(Hn)=1.
Замечание2: Вероятности гипотез определяются до опыта и называются априорными.
.Формула
Байеса. Предположим,
событие А произошло. Какизменятся при
этом вероятности гипотез P(AB)=P(A)*P(B/A),
P(AB)=P(B)P(A/B),
P(AHi)=P(A)P(Hi/A)=P(Hi)P(A/
Hi).
Следовательно P(Hi/A)=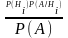 ,
i
=
,
i
=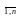 .Заменив
по формуле P(A)=P(H1)P(A/H1)+P(H2)P(A/H2)+…+P(Hn)P(A/Hn)
получим P(Hi/A)=.
Эти формулы называют формулами Байеса.
Они позволяют переоценить вероятности
гипотез после того, как становится
известным результат испытания, в итоге
которого появилось событие А.
.Заменив
по формуле P(A)=P(H1)P(A/H1)+P(H2)P(A/H2)+…+P(Hn)P(A/Hn)
получим P(Hi/A)=.
Эти формулы называют формулами Байеса.
Они позволяют переоценить вероятности
гипотез после того, как становится
известным результат испытания, в итоге
которого появилось событие А.
8 .Ф-я распр. вер.СВ. Определ. и св-ва. Ф-я F(х) наз. ф-я распр. СВ Х, если F(х)=р (Х<х) для всех хє(-∞;+∞)
Х<х означ. -∞<X<x, т.е. ф-я распр. поках. вер. попадания СВ Х на интервалм(-∞;х) левее точки х. Св-ва ф-ции распр:
0≤ F(х)≤1. F(х)=Р(Х<х) ≥0
F(х)-неубывающая. х1<x2, F(х1)≤ F(х2)
A={x<x1} B={x1≤x<x2} C={x<x2} C=A+B AиB- несовм. По теор. слож. им.
Р(С)=P(A)+P(B)= P(X<x1)+P(x1≤x<x2)
P(C)= P(X<x2)=F(x2)
P(X<x1)=F(x1)
P(x1≤x<x2)=F(x2)- F(x1)≥0
F(x2)≥ F(x1) x2>x1
Вер. попадания СВ на полуинтервал х=[x1,x2] P(x1≤x<x2)= F(x2)-F(x1)
4 F(-∞)=0 F(+∞)=1 F(-∞)=lim F(x) F(+∞)=lim F(x) Док-во F(x)=P(X<x), F(-∞)=P(x<-∞)=P()=0, F(+∞)=P(x<+∞)= P(-∞<x<+∞)=P(Ω)=1.
5. F(x)-непрерывна слева,
.Ф-ция распределения ДСВ Ф-ция р ДСВ =F(x)=P(X<X)= Σxi<x P(X=Xi), суммир. ведется по всем х i< x
1)(-∞,х1]эХ 0,x≤x1


х х1 х2 … хn
р р1 р2 … рn
x1 x2 xn
2)х1< x ≤ x2 F(x)= p1,x1<x≤x2
p1+p2, x2<x≤x3
1,x>xn
9 Непрерывные случайные величины
Определение
2: Распределение случайной величины
называется непрерывным, а сама случайная
величина - непрерывной случайной
величиной, если для любого
![]()
![]() где
где
![]() интегрируемая по Лебегу функция. Функция
интегрируемая по Лебегу функция. Функция
![]() называется
плотностью распределения случайной
величины
называется
плотностью распределения случайной
величины
![]()
Теорема
1: Для того чтобы случайная величина
была непрерывной случайной величиной,
необходимо и достаточно, чтобы для
любого
![]() ,
,![]() (1) Замечание 1: Из представления (1)
видно, что функция распределения
непрерывной случайной величины является
непрерывной функцией.. Свойства плотности
распределения:1)
(1) Замечание 1: Из представления (1)
видно, что функция распределения
непрерывной случайной величины является
непрерывной функцией.. Свойства плотности
распределения:1)
![]() ,
2)
,
2)
![]() почти всюду,3)
почти всюду,3)
![]() для
любых х, являющихся точками непрерывности
плотности.. Теорема 2: Для того, чтобы
функция p = p(x) была плотностью распределения
некоторой случайной величины , необходимо
и достаточно, чтобы она удовлетворяла
свойствам 1) и 2) плотности.
для
любых х, являющихся точками непрерывности
плотности.. Теорема 2: Для того, чтобы
функция p = p(x) была плотностью распределения
некоторой случайной величины , необходимо
и достаточно, чтобы она удовлетворяла
свойствам 1) и 2) плотности.
