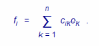- •Ранг матрицы. Вычисление ранга матрицы. Теорема о базисном миноре
- •Элементарные преобразования матрицы. Теорема о ранге матрицы
- •Системы линейных алгебраических уравнений. Основные понятия. Матричная запись системы
- •Критерий совместности системы. Теорема Кронекера – Капелли
- •Доказательство (условия совместности системы) Необходимость
- •Достаточность
- •Теорема Крамера
- •Метод Гаусса решения систем линейных алгебраических уравнений
- •Однородные системы линейных алгебраических уравнений. Свойства решений. Линейная зависимость и линейная независимость решений. Критерий существования нелинейных решений
- •Фундаментальная система решений однородной системы линейных алгебраических уравнений. Структура общего решения системы
- •Неоднородная система линейных алгебраических уравнений. Свойства её решений. Структура общего решения системы
- •Линейные пространства. Определение. Свойства. Примеры линейных пространств
- •Базис и размерность линейного пространства. Теорема о связи базиса и размерности линейного пространства
- •Матрица перехода от одного базиса к другому Преобразование координат при переходе к новому базису
- •Подпространства линейного пространства. Линейная оболочка. Теорема о размерности линейной оболочки
- •Пересечение и сумма подпространств линейного пространства. Прямая сумма подпространств. Разложение пространства в прямую сумму подпространств
- •Линейные операторы. Определение. Свойства
- •Матрица линейного оператора. Единственность матрицы линейного оператора. Преобразование матрицы при переходе к другому базису
- •Образ и ядро линейного оператора. Теорема о размерности образа и ядра линейного оператора
- •Обратный оператор. Критерий его существования
- •1. Теорема Фредгольма (альтернатива).
- •2. Теорема Фредгольма.
- •Собственные значения и собственные векторы линейного оператора
- •Линейная форма — однородный многочлен первой степени, иначе говоря, линейная (однородная) функция на векторном пространстве над полем со значениями в поле Свойства
- •Билинейные формы. Матрица билинейной формы. Её преобразование при переходе к новому базису
- •Квадратичная форма. Приведение к каноническому виду методом Лагранжа
- •Закон инерции квадратичных форм. Критерий Сильвестра положительной определенности квадратичной формы
- •Евклидово пространство. Скалярное произведение. Его свойства
- •Ортонормированный базис. Ортогонализация базиса по Шмидту
- •Произведение квадратичной формы к каноническому виду ортогональным преобразованием
Это утверждение называют теоремой Кронекера-Капелли.
Доказательство (условия совместности системы) Необходимость
Пусть система совместна.
Тогда существуют числа ![]() такие,
что
такие,
что ![]() .
Следовательно, столбец
.
Следовательно, столбец ![]() является
линейной комбинацией столбцов
является
линейной комбинацией столбцов ![]() матрицы
.
Из того, что ранг матрицы не изменится,
если из системы его строк (столбцов)
вычеркнуть или приписать строку
(столбец), которая является линейной
комбинацией других строк (столбцов)
следует, что
матрицы
.
Из того, что ранг матрицы не изменится,
если из системы его строк (столбцов)
вычеркнуть или приписать строку
(столбец), которая является линейной
комбинацией других строк (столбцов)
следует, что ![]() .
.
Достаточность
Пусть ![]() .
Возьмем в матрице
какой-нибудь
базисный минор. Так как
.
Возьмем в матрице
какой-нибудь
базисный минор. Так как ![]() ,
то он же и будет базисным минором и
матрицы
.
Тогда согласно теореме о
базисном миноре последний
столбец матрицы
будет
линейной комбинацией базисных столбцов,
то есть столбцов матрицы
.
Следовательно, столбец свободных членов
системы является линейной комбинацией
столбцов матрицы
.
,
то он же и будет базисным минором и
матрицы
.
Тогда согласно теореме о
базисном миноре последний
столбец матрицы
будет
линейной комбинацией базисных столбцов,
то есть столбцов матрицы
.
Следовательно, столбец свободных членов
системы является линейной комбинацией
столбцов матрицы
.
Теорема Крамера
Рассмотрим систему n линейных алгебраических уравнений относительно n неизвестных
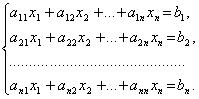
Обозначим Δ, и Δj определитель матрицы системы и определители, полученные из определителя Δ заменой столбца коэффициентов при неизвестном xj столбцом правых частей уравнений системы:
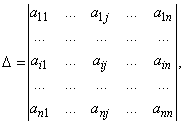
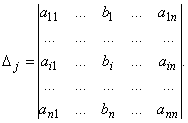
Если определитель матрицы системы отличен от нуля, Δ≠0, то решение системы определяется равенствами:
![]()
Метод Гаусса решения систем линейных алгебраических уравнений
Любая система линейных алгебраических уравнений с помощью элементарных преобразований может быть приведена к каноническому виду:
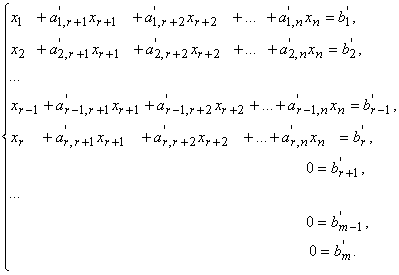
Система линейных уравнений, записанная в каноническом виде, совместна, очевидно, тогда и только тогда, когда b'r+1 = 0, b'r+2 = 0, ..., b'm−1 = 0,b'm = 0.
Общее решение линейной системы, записанной в каноническом виде, очевидно, определяется формулами:
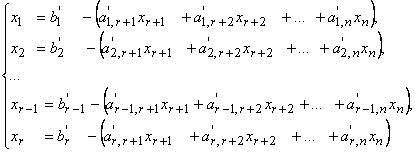
Переменные xr+1 , xr+2 , ..., xm−1, xm могут принимать произвольные значения.
Переменные xr+1 , xr+2 , ..., xm−1, xm называются свободными переменными.
Пременные x1 , x2 , ..., xr−1, xr называются базисными переменными
Однородные системы линейных алгебраических уравнений. Свойства решений. Линейная зависимость и линейная независимость решений. Критерий существования нелинейных решений
Однородной
системой линейных уравнений называется
система вида:
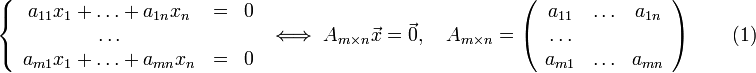
Нулевое
решение ![]() системы
(1) называется тривиальным
решением.
системы
(1) называется тривиальным
решением.
Однородные системы всегда совместны, т.к. всегда существует тривиальное решение.
Если существует любое ненулевое решение системы, то оно называется нетривиальным.
Решения однородной системы обладают свойством линейности:
|
Теорема
(о линейном решении однородных
систем).
Пусть |
|
Сформулируем теорему, которая позволит дать основное определение:
|
Теорема
(о структуре общего решения).
Пусть
|
Фундаментальная система решений однородной системы линейных алгебраических уравнений. Структура общего решения системы
Множество решений однородной линейной системы относительно n неизвестных является линейным подпространством пространства Rn.Размерность этого подпространства равна n − r, где r − ранг матрицы системы A.
Любой базис пространства решений однородной системы линейных уравнений называется фундаментальной системой решений однородной системы.
Иначе говоря, любая упорядоченная совокупность n − r линейно независимых решений однородной линейной системы образует фундаментальную систему решений однородной системы.
Множество K векторов из линейного пространства L называется линейным подпространством пространства L , если сумма x + y любых двух векторов x и y из L принадлежит K и произведение α·x любого любого числа α и любого вектора x и y из L принадлежит K:
![]()
Число k называется размерностью линейного пространства L, если в L существует система из k линейно независимых векторов, а любая система из k+1 вектора — линейно зависима.
Обозначается dimL = k. Пространство L называется k- мерным. Иногда обозначается Lk.
Однородная система линейных алгебраических уравнений
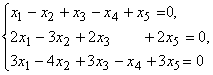
с помощью элементарных преобразований может быть приведена к каноническому виду:
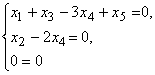
Ранг r матрицы равен 2, число n неизвестных равно 5, система нетривиально совместна. Размерность пространства решений этой однородной системы равна 3: d = n − I = 5 − 2 = 3.
три линейно независимые решения системы

образуют базис пространства решений системы, т.е. образуют её фундаментальную систему решений.
Неоднородная система линейных алгебраических уравнений. Свойства её решений. Структура общего решения системы
Неоднородной системой
линейных уравнений называется
система вида:
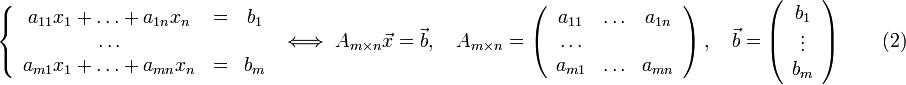
 —
её
расширенная матрица.
—
её
расширенная матрица.
|
Теорема
(об общем решении неоднородных
систем).
Пусть
|
Общее решение неоднородной системы линейных уравнений равно сумме общего решения приведенной однородной системы и любогочастного решения неоднородной системы.
Поскольку общее решение линейной системы, записанной в каноническом виде, определяется формулами:
то общее решение неоднородной системы можно записать в векторной форме в виде:
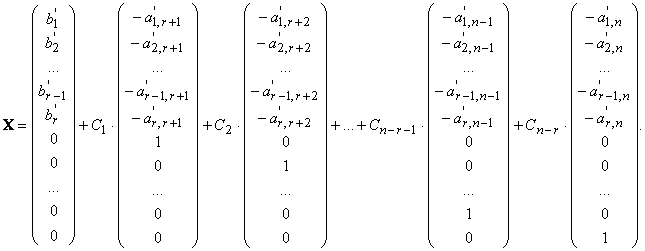
Здесь С1, С2, ..., Сn−r−1, Сn−r — произвольные константы, r — ранг матрицы системы.
Линейные пространства. Определение. Свойства. Примеры линейных пространств
Множество L называется линейным или векторным пространством, если для всех элементов (векторов) этого множества определены операции сложения и умножения на число и справедливо:
1. Каждой паре элементов x и y из L отвечает элемент x + y из L, называемый суммой x и y, причём:
x + y = y + x − сложение коммутативно;
x + (y + z) = (x + y) + z − сложение ассоциативно;
x + 0 = x − существует единственный нулевой элемент 0 ( x + 0 = x для любого x из L);
x + (− x) = 0 − для каждого элемента x из L существует единственный противоположный элемент −x ( x + (−x) = 0 для любого x изL).
2. Каждой паре x и α, где α − число, а x элемент из L, отвечает элемент α·x, наываемый произведением α и x, причём:
α·(β·x) = (α·β)·x − умножнение на число ассоциативно: ;
1·x = x − для любого элемента x из L.
3. Операции сложения и умножения на число связаны соотношениями:
α·(x + y) = α·x + α·y − умножнение на число дистрибутивно относительно сложения элементов;
(α + β)·x = α·x + β·x − умножнение на вектор дистрибутивно относительно сложения чисел.
Примером линейного пространства, является пространство геометрических радиусов-векторов на плоскости L = R2 = { x = x1·i + x2·j}:
x = x1·i + x2· j, y = y1·i + y2· j,
x + y = (x1+ y1)·i + ( x2+ y2)· j, α·x = (αx1)·i + (αx2)· j,
0 = 0·i + 0· j, −x = (−x1)·i +(−x2)· j.
Справедливость остальных аксиом линейного пространства следует из свойств операций сложения и умножения на число действительных чисел.
Простейшие свойства
Векторное пространство является абелевой группой по сложению.
Нейтральный элемент
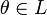 является
единственным, что вытекает из групповых
свойств.
является
единственным, что вытекает из групповых
свойств.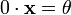 для
любого
для
любого 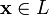 .
.Для любого противоположный элемент
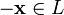 является
единственным, что вытекает из групповых
свойств.
является
единственным, что вытекает из групповых
свойств.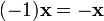 для
любого
.
для
любого
.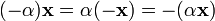 для
любых
для
любых 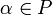 и
.
и
.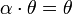 для
любого
.
для
любого
.
Базис и размерность линейного пространства. Теорема о связи базиса и размерности линейного пространства
Система векторов линейного пространства L образует базис в L если эта система векторов упорядочена, линейно независима и любой вектор из L линейно выражается через векторы системы.
Иными словами, линейно независимая упорядоченная система векторов e1, ..., en образует базис в L если любой вектор x из L может быть представлен в виде
x = С1·e1+С2·e2+ ...+Сn· en.
Можно определить базис иначе.
Любая упорядоченная линейно независимая система e1, ..., en векторов n-мерного линейного пространства Ln образует базис этого пространства.
Поскольку n, размерность пространства Ln— максимальное количество линейно независимых векторов пространства, то система векторов x,e1, ..., en линейно зависима и, следовательно, вектор x линейно выражается через векторы e1, ..., en:
x = x1·e1+ x2·e2+ ...+ xn· en.
Такое разложение вектора по базису единственно.
Число k называется размерностью линейного пространства L, если в L существует система из k линейно независимых векторов, а любая система из k+1 вектора — линейно зависима.
Обозначается dimL = k. Пространство L называется k- мерным. Иногда обозначается Lk.
Размерность линейного пространства равна числу базисных векторов.
{Пусть ![]() базис
пространства L
базис
пространства L ![]() Рассмотрим
(n +
1) произвольных элементов
Рассмотрим
(n +
1) произвольных элементов ![]() Разложим
каждый из них по базису {e}
и запишем столбцы полученных коэффициентов
разложения в виде
матрицы An,n+1. Т.к. rangAn,n+1 ≤ n, то,
хотя бы один из столбцов будет линейной
комбинацией остальных
Разложим
каждый из них по базису {e}
и запишем столбцы полученных коэффициентов
разложения в виде
матрицы An,n+1. Т.к. rangAn,n+1 ≤ n, то,
хотя бы один из столбцов будет линейной
комбинацией остальных ![]() элементы aţ –
линейно зависимы
элементы aţ –
линейно зависимы
dimL = n}
Отсюда, в частности, следует, что все базисы одного пространства состоят из одинакового числа векторов.
Матрица перехода от одного базиса к другому Преобразование координат при переходе к новому базису
Пусть ![]() и
и ![]() 2
базиса в линейном пространстве L.
Первый будем считать исходным, а второй
– новым. Все векторы нового базиса
разложим по векторам исходного:
2
базиса в линейном пространстве L.
Первый будем считать исходным, а второй
– новым. Все векторы нового базиса
разложим по векторам исходного:
 или
в матричной форме записи
или
в матричной форме записи ![]()
где 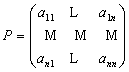 − матрица
перехода от
базиса {e}
к базису {f },
столбцами которой являются координаты
векторов fk в
базисе { e }.
− матрица
перехода от
базиса {e}
к базису {f },
столбцами которой являются координаты
векторов fk в
базисе { e }.
Так
как, по условию, столбцы матрицы P линейно
независимы, ее определитель не равен
нулю и она имеет обратную. Следовательно,
переход от базиса {f}
к базису {e} можно
осуществлять по формуле ![]()
Пусть a –
произвольный элемент из L.
В базисе {e}
он равен: ![]() ,
или, в матричной форме:
,
или, в матричной форме:![]() .
Соответственно, в базисе {f}
имеет место равенство
.
Соответственно, в базисе {f}
имеет место равенство
![]() Отсюда:
Отсюда: ![]()
![]() Подставляя
Подставляя ![]() из
формулы перехода, получим:
из
формулы перехода, получим:
![]() Т.к. а произвольный
вектор L ,
имеем:
Т.к. а произвольный
вектор L ,
имеем:
![]() формула
пересчета новых
координат в старые и
формула
пересчета новых
координат в старые и
![]() формула
пересчета старых
координат в новые.
формула
пересчета старых
координат в новые.
(При
выводе было использовано утверждение: ![]() )
)
Таким
образом, для вычисления координат в
новом базисе приходится решать СЛАУ
относительно этих координат: ![]()
Подпространства линейного пространства. Линейная оболочка. Теорема о размерности линейной оболочки
Определение 1. Подпространством линейного пространства L называется такое подмножество
элементов L, которое само является линейным пространством.
Т.е. подпространство замкнуто относительно операций сложения и умножения на число. (все аксиомы выполняются автоматически).
Примеры. ![]() ,
множество решений однородной СЛАУ.
,
множество решений однородной СЛАУ.
Определение
2. Линейной
оболочкой системы
элементов ![]() ,
принадлежащих L ,
называется совокупность всех линейных
комбинаций этих элементов:
,
принадлежащих L ,
называется совокупность всех линейных
комбинаций этих элементов: ![]() .
.
Непосредственно из определения следует, что любая линейная оболочка является линейным пространством, а любое линейное пространство – линейной оболочкой натянутой на какой-либо базис этого пространства.
Теорема 1 (основное свойство линейных оболочек). Любой вектор системы , линейно зависящий от остальных, можно исключить без изменения линейной оболочки.
{Пусть,
для определенности, ![]() а
а ![]() произвольный
. Тогда
произвольный
. Тогда
![]() ,
т.е.
,
т.е. ![]() }
}
Следствие. Размерность
линейной оболочки равна рангу
соответствующей системы элементов:![]()
Пересечение и сумма подпространств линейного пространства. Прямая сумма подпространств. Разложение пространства в прямую сумму подпространств
Пусть L1 и L2 — два произвольных подпространства одного и того же линейного пространства R. Совокупность всех элементов х пространства R, принадлежащих одновременно L1 и L2, образует подпространство пространства R (Ибо элементы этой совокупности удовлетворяют требованиям 1° и 2°, сформулированным в начале п. 1), называемое пересечением подпространств L1 и L2. Совокупность всех элементов пространства R вида у + z, где у — элемент подпространства L1, a z — элемент подпространства L2, образует подпространство пространства R, называемое суммой подпространств L1 и L2. Пример. Пусть R — линейное пространство всех свободных векторов (в трехмерном пространстве), L1 — подпространство всех свободных векторов, параллельных плоскости Оху, L2 — подпространство всех свободных векторов, параллельных плоскости Oxz. Тогда суммой подпространств L1 и L2 будет являться все пространство R, а пересечением подпространств L\ и L2 будет являться множество всех свободных векторов, параллельных оси Ох. Справедливо следующее утверждение. Теорема 2.9. Сумма размерностей произвольных подпространств L1 и L2 конечномерного линейного пространства R равна сумме размерности пересечения этих подпространств и размерности суммы этих подпространств.
Прямая сумма — производный математический объект, создаваемый по определённым ниже правилам из базовых объектов. В качестве базовых чаще всего выступают векторные пространства или абелевы группы. Существует также обобщение данной конструкции для банаховых и гильбертовых пространств.
Говорят,
что линейное
пространство ![]() есть прямая
сумма своих подпространств
есть прямая
сумма своих подпространств ![]() :
:
![]()
если
каждый вектор ![]() представляется
в виде суммы
представляется
в виде суммы
![]()
и притом единственным образом.
Понятие
прямой суммы ![]() распространяется
на случай, когда
изначально
не являются подпространствами какого-либо
одного объемлющего линейного пространства.
распространяется
на случай, когда
изначально
не являются подпространствами какого-либо
одного объемлющего линейного пространства.
Определим
как декартово
произведение ![]() и
определим в нём операции линейного
пространства с помощью формул
и
определим в нём операции линейного
пространства с помощью формул
![]()
Тогда
является
линейным пространством, содержащим
подпространства ![]() Согласно
построению, каждый вектор
однозначно
представим в виде
Согласно
построению, каждый вектор
однозначно
представим в виде ![]()
![]() следовательно,
следовательно, ![]()
Линейные операторы. Определение. Свойства
Оператором называется правило, по которому каждому элементу x некоторого непустого множества X ставится в соответствие единственный элемент y некоторого непустого множества Y. Говорят, что оператор действует из X в Y.
Действие оператора обозначают y = A(x), y — образ x, x — прообраз y.
Если каждый элемнт y из Y имеет единственный прообраз x из X, y= A(x), оператор называют взаимно однозначным отображением X в Y или преобразованием X, X — область определения оператора.
Пусть X и Y два линейные пространства. Оператор A, действующий из X в Y, называется линейным оператором, если для любых двух элементов u и v из X и любого числа α справедливо:
A(u + v) = A(u ) + A(v) , A(α·u) = α· A(u).
Матрица линейного оператора. Единственность матрицы линейного оператора. Преобразование матрицы при переходе к другому базису
Линейный оператор A действует из n-мерного линейного пространства X в m-мерное линейное пространство Y .
В этих пространствах определены базисы e = {e1, ..., en} и f = {f1, ..., fm}.
Пусть A(ei ) = a1i·f1 + a2i·f2 + ...+ ami·fm — разложение образа i-го базисного вектора базиса e пространства X по базису f пространства Y, i = 1, 2, ..., n.
Матрицей линейного оператора в базисах e, f называется матрица A, столбцами которой являются координаты образов базисных векторов базиса e в базисе f , A = {aij}= {A(ej )i}:

Координаты образа y = A(x) и прообраза x связаны соотношеннием:
y = A· x,
![]()

Образ
вектора х равен
произведению матрицы линейного оператора
на столбец его координат:
если у
= А(х), то 

Таким образом, каждому линейному оператору ставится в соответствие матрица.
При
переходе к новому базису матрица
линейного оператора меняется
по следующему
закону: ![]()
{Пусть
{f}
– новый базис, {e}
– старый. 1) ![]() (§5,8);
(§5,8);
2) ![]() }
}
Следствие. Определитель матрицы линейного оператора не зависит от базиса.
{![]() }
}
Образ и ядро линейного оператора. Теорема о размерности образа и ядра линейного оператора
Определение
1. Функция
(отображение) А, определенная на линейном
пространстве Ln ,
область значений которой принадлежит
линейному пространству Lm (здесь n и m –
размерности соответствующих пространств)
называется оператором : ![]()
Если ![]()
Все
прообразы нулевого элемента Lm называют
ядром оператора А: ![]()
Рассмотрим линейный оператор A, действующий в пространстве Rn.
Напомним, что множество элементов пространства Rn, которые являются образами элементов из области определения D(A) оператора A, называют образом оператора A и обозначают Im(A).
Теорема. Образ Im(A) линейного оператора A — линейное подпространство пространства Rn.
Определение. Размерность образа линейного оператора называется рангом оператора, обозначается Rg(A): r=Rg(A)=dim Im(A).
Определение. Ядром
линейного оператора называется множество
элементов пространства Rn,
образом которых является нулевой
элемент. Ядро оператора обозначают
Ker(A): ![]() .
.
Теорема. Ядро линейного оператора — линейное подпространство пространства Rn.
Определение. Размерность ядра линейного оператора называется дефектом оператора, обозначается def(A):r=def(A)=dimKer(A).
Для линейного
оператора![]() ,
действующего в пространстве Rn,
справедливы следующие утверждения:
,
действующего в пространстве Rn,
справедливы следующие утверждения:
1) ранг оператора равен рангу его матрицы;
2) ядро оператора совпадает с множеством решений линейной однородной системы с матрицей A, размерность пространства решений этой системы равна дефекту оператора, а ее фундаментальная система решений образует базис в ядре оператора;
столбцы, входящие в базисный минор матрицы оператора образуют базис в образе оператора.
Эти утверждения позволяют описать структуру образа и ядра линейного оператора (найти размерность подпространства и построить его базис), заданного матрицей, на языке матричных преобразований и общей теории линейных систем.
Примеры.
1. Ядро
и образ нулевого
оператора:
поскольку ![]() то
то ![]()
2. Ядро
и образ тождественного (единичного)
оператора:поскольку ![]() ,
то
,
то ![]()
3. Ядро
и образ оператора проектирования
пространства Rn на
подпространство Rn-1 параллельно
вектору ![]() :
поскольку
:
поскольку ![]() ,
то
,
то ![]()
4. Ядро
и образ оператора поворота пространства R3 против
часовой стрелки на угол p относительно
оси вектора ![]() :
поскольку
:
поскольку ![]() ,
то
,
то ![]()
Обратный оператор. Критерий его существования
Пусть А –
линейный оператор. Будем говорить,
что А имеет обратный,
если для каждого ![]() существует
точно одно
существует
точно одно ![]() ,
такое что
,
такое что ![]() .
При этом под обратным понимается оператор
с областью определения
.
При этом под обратным понимается оператор
с областью определения ![]() и
множество значений D(A),
заданный соотношением
и
множество значений D(A),
заданный соотношением ![]() где
.
где
.
Вопрос существования обратного оператора – это вопрос об условиях разрешимости операторного уравнения
|
(2) |
В конечномерном случае эти условия формулировала альтернатива Фредгольма.
1. Теорема Фредгольма (альтернатива).
Если
уравнение ![]() имеет
только тривиальное решение, то уравнение
(2) разрешимо единственным образом
при любой правой части.
имеет
только тривиальное решение, то уравнение
(2) разрешимо единственным образом
при любой правой части.
2. Теорема Фредгольма.
Если
уравнение
имеет
нетривиальное решение, то (2) разрешимо
(заведомо не единственным образом) тогда
и только тогда, когда ![]() ортогональна
всем решениям сопряженной однородной
задачи.
ортогональна
всем решениям сопряженной однородной
задачи.
Собственные значения и собственные векторы линейного оператора
Рассмотрим линейный оператор A, действующий в линейном пространстве X: y = A(x), ∀x ∈ X, y ∈ X.
Число λ называется собственным значением оператора A, если существует такой ненулевой вектор x, что справедливо равенство A(x) = λ·x. Любой ненулевой вектор x ≠0, удовлетворяющий этому уравнению, называется собственным вектором оператора A, отвечающим собственному значению λ.
A(x) = λ·x, x ≠0, x ∈ X.
Пусть A квадратная матрица. Число λ называется собственным значением матрицы A, если существует такой ненулевой вектор x, что справедливо равенство A·x = λ·x. Любой ненулевой вектор x ≠0, удовлетворяющий этому уравнению, называется собственным вектором матрицы A, отвечающим собственному значению λ.
A·x = λ·x, x ≠0.
Для того чтобы ненулевой вектор x был собственным вектором квадратной матрицы A, отвечающим собственному значению λ, необходимо и достаточно, чтобы этот вектор был нетривиальным решением однородной системы линейных уравнений (A − λ·E)·x = 0, x ≠0. Здесь E −единичная матрица
Линейная форма. Преобразование коэффициентов линейной формы при переходе к новому базису
Линейная форма — однородный многочлен первой степени, иначе говоря, линейная (однородная) функция на векторном пространстве над полем со значениями в поле Свойства
Множество
всех линейных форм на
является
линейным пространством относительно
операций сложения и умножения на элемент
из
.
Это пространство называетсясопряженным к
и
обозначается ![]() .
.
Ядро линейной формы (линейного функционала) — линейное пространство. В невырожденном случае оно является гиперплоскостью.
В
частности, при ![]() ядро
линейного функционала
ядро
линейного функционала ![]() —
плоскость в трёхмерном пространстве,
причем коэффициенты функционала суть
координаты нормального вектора плоскости
—
плоскость в трёхмерном пространстве,
причем коэффициенты функционала суть
координаты нормального вектора плоскости
Преобразование коэффициентов линейной формы при переходе к новому базису.
Пусть даны два базиса e1, e2, … , en и f1, f2, … , fn , связанные матрицей перехода C = (cik) по формуле
|
|
|
Тогда
|
|
|
где 'i — коэффициенты линейной формы в базисе f1, f2, … , fn .
Или в матричной форме:
f = e · C ' = C · .
Отметим, что коэффициенты линейной формы преобразуются так же, как базисные векторы — посредством матрицы C . В то время как координаты векторов преобразуются посредством матрицы C − 1 .
Ядро линейной формы (линейного функционала) — линейное пространство. Оно называется гиперплоскостью.
В частности, при n = 3 ядро линейного функционала 1x + 2y + 3z = 0 — плоскость в трехмерном пространстве, причем коэффициенты функционала суть координаты нормального вектора плоскости
Билинейные формы. Матрица билинейной формы. Её преобразование при переходе к новому базису
Билинейной
формой называется функция ![]() ,
линейная по каждому из аргументов:
,
линейная по каждому из аргументов:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
здесь ![]() и
и ![]()
Пусть e1, ..., en — базис в L. И пусть для векторов x и y из L заданы разложения
x = x1·e1+x2·e2+ ...+ xn· en и y = y1·e1+ y2·e2+ ...+ yn· en .
Тогда для билинейной формы φ(x , y) справедливо представление
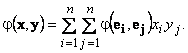
Обозначим φi j = φ(ei , ej). Тогда для билинейной формы формы φ(x , y) справедливо матричное представление φ(x , y) = x T·Φ·y:
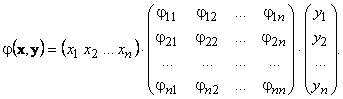

Матрица Φ называется матрицей билинейной формы.
Ранг матрицы билинейной формы не зависит от выбора базиса и называется рангом билинейной формы.
Дефектом билинейной формы называется разность между размерностью пространства и рангом билинейной формы: d = n − r.
Билинейная форма называется невырожденной, если её дефект равен нулю.
Преобразование матрицы билинейной формы при замене базиса
Матрица, представляющая билинейную форму в новом базисе, связана с матрицей, представляющей её в старом базисе, через матрицу, обратную матрице перехода к новому базису (матрице Якоби), через которую преобразуются координаты векторов.
Иными
словами, если координаты вектора в
старом базисе ![]() выражаются
через координаты в новом
выражаются
через координаты в новом ![]() через
матрицу
через
матрицу ![]()
![]() ,
или в матричной записи
,
или в матричной записи ![]() ,
то билинейная форма
,
то билинейная форма ![]() на
любых векторах
на
любых векторах ![]() и
и ![]() запишется,
как
запишется,
как
![]() ,
,
то есть компоненты матрицы, представляющей билинейную форму в новом базисе, будут:
![]() ,
,
или, в матричной записи:
![]() ,
,
![]() ,
где
,
где ![]() —
матрица прямого преобразования
координат
—
матрица прямого преобразования
координат ![]() .
.
Квадратичная форма. Приведение к каноническому виду методом Лагранжа
Квадратичная форма — функция на векторном пространстве, задаваемая однородным многочленом второй степени от координат вектора.
Определение
Пусть ![]() есть векторное
пространство над
полем
есть векторное
пространство над
полем ![]() и
и ![]() —
базис в
.
—
базис в
.
Функция ![]() называется
квадратичной формой, если её можно
представить в виде
называется
квадратичной формой, если её можно
представить в виде
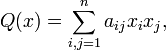
где ![]() ,
а
,
а ![]() —
некоторые элементы поля
.
—
некоторые элементы поля
.
Пусть e1, ..., en — базис в L. И пусть для вектора x из L задано разложение x = x1·e1+x2·e2+ ...+ xn· en.
Тогда для квадратичной формы k(x) справедливо представление
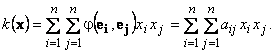
Здесь φ(ei , ej ) — значение полярной для k(x) билинейной формы φ(x , y).
Матрица A = {aij} называется матрицей квадратичной формы. Определённая таким образом матрица квадратичной формы является симметричной матрицей.
Метод Лагранжа — метод приведения квадратичной формы к каноническому виду, указанный в 1759 году Лагранжем.
Описание
Данный метод состоит в последовательном выделении в квадратичной форме полных квадратов. Пусть
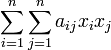
есть данная квадратичная форма. Возможны два случая:
хотя бы один из коэффициентов
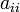 при
квадратах отличен от нуля. Не нарушая
общности, будем считать
при
квадратах отличен от нуля. Не нарушая
общности, будем считать 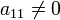 (этого
всегда можно добиться соответствующей
перенумерацией переменных);
(этого
всегда можно добиться соответствующей
перенумерацией переменных);все коэффициенты
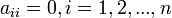 ,
но есть коэффициент
,
но есть коэффициент 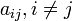 ,
отличный от нуля (для определённости
пусть будет
,
отличный от нуля (для определённости
пусть будет 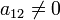 ).
).
В первом случае преобразуем квадратичную форму следующим образом:
![]()
![]()
![]() ,
где
,
где
![]() ,
а через
,
а через ![]() обозначены
все остальные слагаемые.
обозначены
все остальные слагаемые.
![]() представляет
собой квадратичную форму от n-1 переменных
представляет
собой квадратичную форму от n-1 переменных ![]() .
.
С ней поступают аналогичным образом и так далее.
Заметим,
что ![]()
Второй
случай заменой переменных ![]() сводится
к первому.
сводится
к первому.
Закон инерции квадратичных форм. Критерий Сильвестра положительной определенности квадратичной формы
Пусть k(x) — квадратичная форма, заданная в пространстве арифметических векторов Rn.
В пространстве Rn существует канонический базис квадратичной формы, базис, в котором матрица квадратичной формы является диагональной.
В этом базисе квадратичная форма имеет канонический вид
k(x) = λ1x12 + λ2x22 + ... + λnxn2.
Числа λ1, λ2, ... , λn — канонические коэффициенты квадратичной формы.
Закон инерции квадратичных форм гласит: число положительных, отрицательных и нулевых канонических коэфициентов квадратичной формы не зависит от преобразования, с помощью которого квадатичная форма приводится к каноническому виду.
Число положительных канонических коэфициентов квадратичной формы называется положительным индексом инерции квадратичной формы. Число отрицательных канонических коэфициентов квадратичной формы называется отрицательным индексом инерции квадратичной формы. Разность между положительным и отрицательным индексами квадратичной формы наз ывается сигнатурой квадратичной формы. Число ненулевых канонических коэффициентов называется рангом квадратичной формы.
Критерий Сильвестра определяет, является ли симметричная квадратная матрица положительно (отрицательно, неотрицательно) определённой.
Пусть квадратичная форма имеет в каком-то базисе матрицу
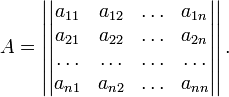
Тогда
эта форма положительно определена, если
и только если все её главные
(угловые) миноры ![]() положительны.
Форма отрицательно определена, если и
только если знаки
чередуются,
причём
положительны.
Форма отрицательно определена, если и
только если знаки
чередуются,
причём ![]() .
Здесь главными минорами
матрицы
называются
определители вида
.
Здесь главными минорами
матрицы
называются
определители вида
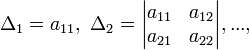

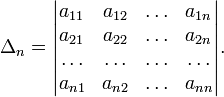
Для неотрицательно определённых матриц критерий действует только в одну сторону: если форма неотрицательно определена, то главные миноры неотрицательны. Обратное неверно. Например, матрица
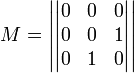
не
является неотрицательно определённой —
так как, например, ![]() для
для ![]() .
В то же время все её главные миноры равны
0, то есть неотрицательны.
.
В то же время все её главные миноры равны
0, то есть неотрицательны.
Евклидово пространство. Скалярное произведение. Его свойства
Определение
1. Линейное
пространство E =
{f, g, h,
…} называется евклидовым, если ![]()
ставится в
соответствие число,
называемое скалярным
произведением:![]() .
При этом, для
.
При этом, для ![]() выполняются
аксиомы:
выполняются
аксиомы:
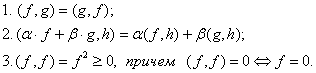
Имеет место
Неравенство
Коши – Буняковского – Шварца:![]()
{![]() }
}
По
определению, длиной элемента называется:![]() ,
а косинусом угла между двумя элементами:
,
а косинусом угла между двумя элементами:![]() (В
силу неравенства К – Б – Ш это
определение корректно)
(В
силу неравенства К – Б – Ш это
определение корректно)
Отсюда
легко получить, что ![]()
Примеры.
1) 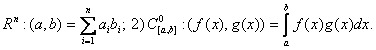
Определение
2. Линейное
пространство N называется нормированным,
если ![]() N ставится
N ставится
в
соответствие число ![]() ,
называемое нормой элемента
,
называемое нормой элемента ![]() , и удовлетворяющее
условиям:
, и удовлетворяющее
условиям:
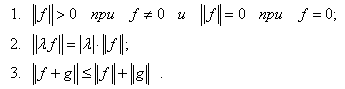
Свойство (3) называется неравенством треугольника, а норма есть обобщение понятия ‘длина’.
Примеры.
1) Абсолютная
норма: ![]()
2)Средняя
или евклидова норма: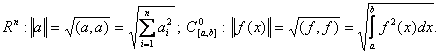
В
нормированных евклидовых пространствах
косинус угла между векторами обычно
записывают в виде ![]()
1.
Конечномерное гильбертово
пространство,
то есть конечномерное вещественное векторное
пространство ![]() с
введённым на нём (положительно
определенным) скалярным
произведением,
порождающим норму:
с
введённым на нём (положительно
определенным) скалярным
произведением,
порождающим норму:
![]() ,
,
в простейшем случае (евклидова норма):
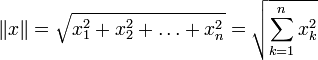
где ![]() (в
евклидовом пространстве всегда можно
выбрать базис,
в котором верен именно этот простейший
вариант).
(в
евклидовом пространстве всегда можно
выбрать базис,
в котором верен именно этот простейший
вариант).
2. Метрическое пространство, соответствующее пространству описанному выше. То есть с метрикой, введённой по формуле:
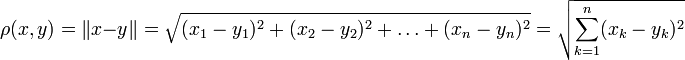 ,
,
где
и ![]() .
.
Ортонормированный базис. Ортогонализация базиса по Шмидту
Определение
1. Система
векторов евклидова пространства {![]() }
называется ортогональной, если все ее
элементы попарно ортогональны:
}
называется ортогональной, если все ее
элементы попарно ортогональны: ![]()
Теорема 1. Ортогональная система неравных нулю векторов линейно независима.
{Предположим,
система линейно зависима: ![]() и,
для определенности,
и,
для определенности, ![]() Умножим
скалярно равенство на
Умножим
скалярно равенство на ![]() .
Учитывая ортогональность системы,
получим:
.
Учитывая ортогональность системы,
получим: ![]() }
}
Определение 2. Система векторов евклидова пространства { } называется ортонормированной, если она ортогональна и норма каждого элемента равна единице.
Из теоремы 1 сразу следует, что ортонормированная система элементов всегда линейно независима. Отсюда, в свою очередь, следует, что в n – мерном евклидовом пространстве ортонормированная система из n векторов образует базис (например, {i , j , k} в 3х – мерном пространстве). Такая система называется ортонормированным базисом, а ее векторы – базисными ортами.
Координаты
вектора в ортонормированном
базисе можно легко вычислить с помощью
скалярного произведения:
если ![]() Действительно, умножая
равенство
Действительно, умножая
равенство ![]() на
на ![]() ,
получаем указанную формулу.
,
получаем указанную формулу.
Вообще,
все основные величины: скалярное
произведение векторов, длина вектора,
косинус угла между векторами и т.д. имеют
наиболее простой вид в ортонормированном
базисе. Рассмотрим скалярное
произведение: ![]() ,
так как
,
так как
![]() а
все остальные слагаемые равны нулю.
Отсюда сразу получаем:
а
все остальные слагаемые равны нулю.
Отсюда сразу получаем: ![]() ,
,
![]()
*
Рассмотрим произвольный базис ![]() .
Скалярное произведение в этом базисе
будет равно:
.
Скалярное произведение в этом базисе
будет равно: ![]() (Здесь αi и βj –
(Здесь αi и βj –
координаты
векторов в базисе {f},
а ![]() –
скалярные произведения базисных
векторов).
–
скалярные произведения базисных
векторов).
Величины γij образуют
матрицу G,
называемую матрицей
Грама. Скалярное
произведение в матричной форме будет
иметь вид: ![]() *
*
Теорема 2. В любом n – мерном евклидовом пространстве существует ортонормированный базис. Доказательство теоремы носит конструктивный характер и носит название
Процесс ортогонализации Грама – Шмидта.
Пусть ![]() −
произвольный базис n –
мерного евклидова пространства
(существование такого базиса обусловлено n –
мерностью пространства). Алгоритм
построения по данному базису
ортонормированного заключается в
следующем:
−
произвольный базис n –
мерного евклидова пространства
(существование такого базиса обусловлено n –
мерностью пространства). Алгоритм
построения по данному базису
ортонормированного заключается в
следующем:
![]()
![]()
![]()
![]()
![]()
![]() Аналогично
Аналогично ![]()
![]()
Продолжая
процесс, получаем ортонормированный
базис ![]() , где
, где
![]()
Замечание. С помощью рассмотренного алгоритма можно построить ортонормированный базис любой линейной оболочки, например, ортонормированный базис линейной оболочки системы, имеющей ранг равный трем и состоящей из пятимерных векторов.
Пример. ![]()
Произведение квадратичной формы к каноническому виду ортогональным преобразованием
Приведение квадратичной формы к каноническому виду ортогональным преобразованием переменных. Теорема 9. Если существует ортогональное преобразование с матрицей С, приводящее действительную квадратичную форму f (x1,x2…,xn) к каноническому виду: φ (y1, y2….yn)= λ1y21+λ2y22+λny2n (1.11), то λ1, λ2,…. λn — характеристические числа матрицы А квадратичной формы f. Теорема 10. Для любой действительной квадратичной формы существует ортогональное преобразование, приводящее ее к каноническому виду. Теорема 11. Для любой действительной симметрической матрицы А существует такая ортогональная матрица Т, что Т-1АТ - диагональная матрица. С помощью матрицы В записываем искомое ортогональное преобразование x1= √3/5 y1 + √2/5 y2, x1= 1/√5(√3y1 + √2y2) или x2= √2/5 y1 + √3/5 y2, x2 = 1/√5 (- √2y1 + √3y2). Это преобразование приводит данную квадратичную форму к каноническому виду φ (y1, y2) = y21+ 11y22.