1. Ранг матрицы. Вычисление ранга матрицы. Теорема о базисном миноре

2. Элементарные преобразования матрицы. Теорема о ранге матрицы

3. Системы линейных алгебраических уравнений. Основные понятия. Матричная запись системы

4. Критерий совместности системы. Теорема Кронекера – Капелли

5. Теорема Крамера

6. Метод Гаусса решения систем линейных алгебраических уравнений

7. Однородные системы линейных алгебраических уравнений. Свойства решений. Линейная зависимость и линейная независимость решений. Критерий существования нелинейных решений

8. Фундаментальная система решений однородной системы линейных алгебраических уравнений. Структура общего решения системы

9. Неоднородная система линейных алгебраических уравнений. Свойства её решений. Структура общего решения системы

10. Линейные пространства. Определение. Свойства. Примеры линейных пространств

11. Базис и размерность линейного пространства. Теорема о связи базиса и размерности линейного пространства

12. Матрица перехода от одного базиса к другому Преобразование координат при переходе к новому базису

13. Подпространства линейного пространства. Линейная оболочка. Теорема о размерности линейной оболочки

14. Пересечение и сумма подпространств линейного пространства. Прямая сумма подпространств. Разложение пространства в прямую сумму подпространств

15. Линейные операторы. Определение. Свойства

16. Матрица линейного оператора. Единственность матрицы линейного оператора. Преобразование матрицы при переходе к другому базису

17. Образ и ядро линейного оператора. Теорема о размерности образа и ядра линейного оператора

18. Обратный оператор. Критерий его существования

19. Собственные значения и собственные векторы линейного оператора

20. Линейные форма. Преобразование коэффициентов линейной формы при переходе к новому базису

21. Билинейные формы. Матрица билинейной формы. Её преобразование при переходе к новому базису

22. Квадратичная форма. Приведение к каноническому виду методом Лагранжа

23. Закон инерции квадратичных форм. Критерий Сильвестра положительной определенности квадратичной формы

24. Евклидово пространство. Скалярное произведение. Его свойства

25. Ортонормированный базис. Ортогонализация базиса по Шмидту

26. Произведение квадратичной формы к каноническому виду ортогональным преобразованием

1. Ранг матрицы. Вычисление ранга матрицы. Теорема о базисном миноре

Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля.

Пусть   — прямоугольная матрица.

Тогда по определению рангом матрицы   является:

• ноль, если   — нулевая матрица;

• число 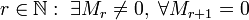 , где   — минор матрицы   порядка  , а 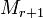  — окаймляющий к нему минор порядка 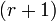 , если они существуют.

Теорема (о корректности определения рангов). Пусть все миноры матрицы   порядка 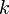  равны нулю (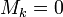 ). Тогда 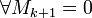 , если они существуют.

Связанные определения

• Ранг   матрицы   размера 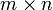  называют полным, если  .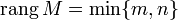

• Базисный минор матрицы   — любой ненулевой минор матрицы   порядка  , где  .

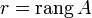  • Строки и столбцы, на пересечении которых стоит базисный минор, называются базисными строками и столбцами. (Они определены неоднозначно в силу неоднозначности базисного минора.)

Свойства

• Теорема (о базисном миноре): Пусть 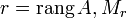  — базисный минор матрицы  , тогда:

  1. базисные строки и базисные столбцы линейно независимы;

  2. любая строка (столбец) матрицы   есть линейная комбинация базисных строк (столбцов).

• Следствия:

1. Если ранг матрицы равен  , то любые 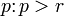  строк или столбцов этой матрицы будут линейно зависимы.

2. Если   — квадратная матрица, и 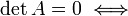 , то строки и столбцы этой матрицы линейно зависимы.

3. Пусть  , тогда максимальное количество линейно независимых строк (столбцов) этой матрицы равно  .

Минор   матрицы   ― определитель такой квадратной матрицы   порядка   (который называется также порядком этого минора), элементы которой стоят в матрице   на пересечении строк с номерами   и столбцов с номерами  .

Ранг матрицы находится путем преобразования матрицы в треугольный вид и ранг матрицы равен разности количества строк в исх матрице,минус количество ненулевых в треугольной.

2. Элементарные преобразования матрицы. Теорема о ранге матрицы

Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц. Таким образом, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.

Элементарными преобразованиями строк называют:

• перестановка местами любых двух строк матрицы;

• умножение любой строки матрицы на константу  ,  ;

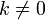• прибавление к любой строке матрицы другой строки.

В некоторых курсах линейной алгебры перестановка строк матрицы не выделяется в отдельное элементарное преобразование в силу того перестановку местами любых двух строк матрицы можно получить используя умножение любой строки матрицы на константу  ,   и прибавление к любой строке матрицы другой строки, умноженной на константу  ,  .

Аналогично определяются элементарные преобразования столбцов.

Элементарные преобразования обратимы.

Обозначение   указывает на то, что матрица   может быть получена из   путём элементарных преобразований (или наоборот).

Теорема о ранге матрицы - ранг матрицы А является наибольшим таким числом числом r, что в матрице А имеется r строк (r столбцов), образующих линейно – независимую систему.