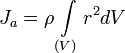18. Момент импульса и закон его сохранения Момент импульса

При сравнении законов поступательного и вращательного движений видна аналогия между ними. Во вращательном движении аналогом силы становится ее момент, аналог массы - момент инерции. Какая же величина будет аналогом импульса тела? Это момент импульса тела относительно оси.  Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:    где r - радиус-вектор, проведенный из точки О в точку A, p=mv - импульс материальной точки (рис. 1); L - псевдовектор, направление которого совпадает с направлением поступательного движения правого винта при его вращении от r к р.

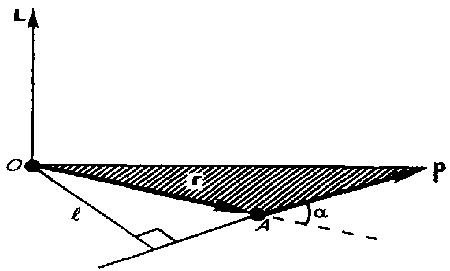
Рис.1

Модуль вектора момента импульса    где α - угол между векторами r и р, l - плечо вектора р относительно точки О.  Моментом импульса относительно неподвижной оси z называется скалярная величина L_z, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Момент импульса L_z не зависит от положения точки О на оси z.  При вращении абсолютно твердого тела вокруг неподвижной оси z каждая точка тела движется по окружности постоянного радиуса r_iсо скоростью v_i . Скорость v_i и импульс m_iv_i перпендикулярны этому радиусу, т. е. радиус является плечом вектора m_iv_i . Значит, мы можем записать, что момент импульса отдельной частицы равен  (1)  и направлен по оси в сторону, определяемую правилом правого винта.  Монет импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц: 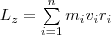   Используя формулу v_i = ωr_i, получим 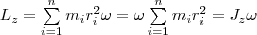   т. е.   2)  Таким образом, момент импульса твердого тела относительно оси равен моменту инерции тела относительно той же оси, умноженному на угловую скорость. Продифференцируем уравнение (2) по времени:    т. е.    Эта формула - еще одна форма уравнения динамики вращательного движения твердого тела относительно неподвижной оси: производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси.  Можно показать, что имеет место векторное равенство  (3)  В замкнутой системе момент внешних сил   и   откуда   (4)  Выражение (4) представляет собой закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т. е. не изменяется с течением времени.  Закон сохранения момента импульса также как и закон сохранения энергии является фундаментальным законом природы. Он связан со свойством симметрии пространства - его изотропностью, т. е. с инвариантностью физических законов относительно выбора направления осей координат системы отсчета (относительно поворота замкнутой системы в пространстве на любой угол)

Вопрос 19 момент инерции, Теорема Штейнера

Момент инерции относительно неподвижной оси – величина, равная произведению массы тела на квадрат расстояния до рассматриваемой оси

Th Штейнера: момент инерции тела   относительно произвольной оси равен сумме момента инерции этого тела   относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела   на квадрат расстояния  а  между осями:

J = J_c + ma²

где

 — известный момент инерции относительно оси, проходящей через центр масс тела,

 — искомый момент инерции относительно параллельной оси,

 — масса тела,

a — расстояние между указанными осями.

Если масса тела распределена неравномерно, то:

J= интеграл (r² dm)

А вообще: J= mR²/2

тело	Положение оси	Момент инерции
Полый тонкостенный цилиндр	Ось симметрии	mR2
Сплошной цилиндр/ таблетка		½ mR2
Прямой тонкий стержень	Перпендикулярно стержню	1/12ml2
Шар радиусом R	Через центр шара	2/5 mR2

20.

Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости). Обозначение: I или J.

Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:

mi — масса i-й точки,

ri — расстояние от i-й точки до оси.

Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.

где:

— масса малого элемента объёма тела ,

• — плотность,

• — расстояние от элемента до оси a.

Если тело однородно, то есть его плотность всюду одинакова, то