Расчетно-графическая работа [12 вариант]

вариант №12

1. Решить матричным способом

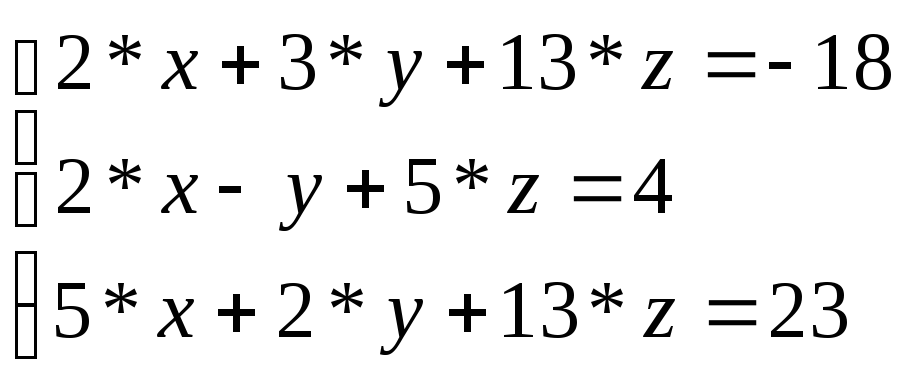
Решение.

Перепишем систему в виде ,

где

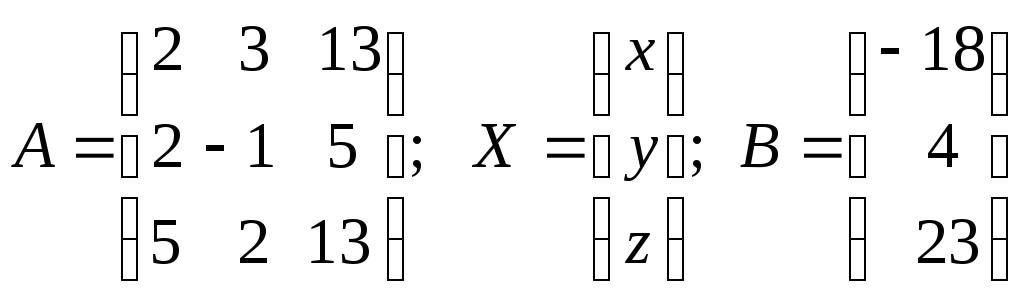
Решение матричного уравнения имеет вид .

Найдём .

.

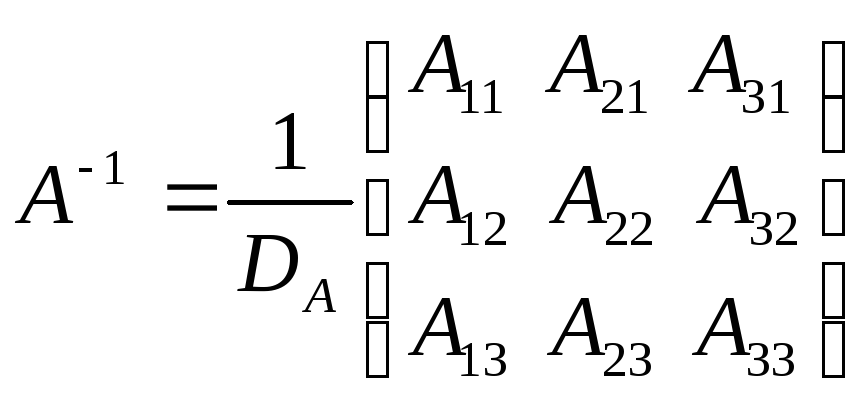Имеем

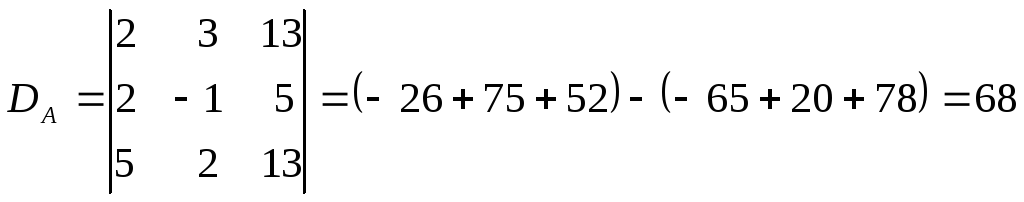
Вычислим алгебраические дополнения элементов этого определителя:

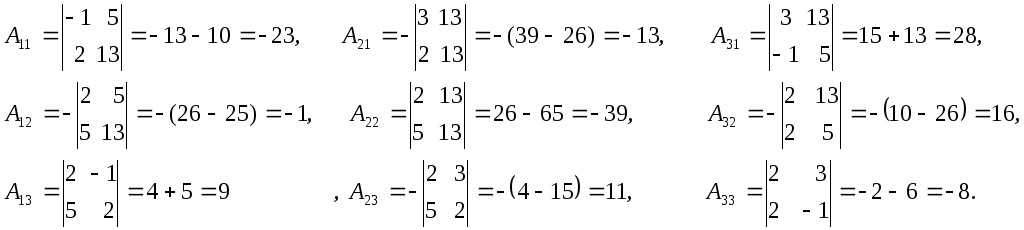
Таким образом,

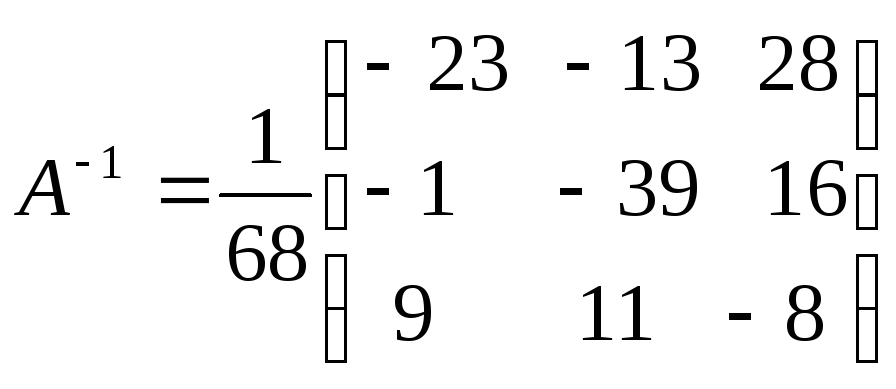
откуда

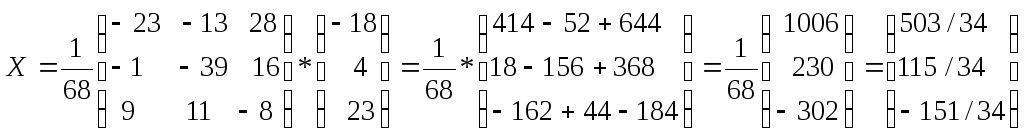
Ответ:

3. Коллинеарны ли векторы и .

Решение.

Условие коллинеарности .

Условие коллинеарности не выполняется. .

Следовательно, векторы неколлинеарны.

4. Исследовать систему на линейную зависимость.

.

Решение.

Условие линейной зависимости: определитель матрицы системы равен нулю.

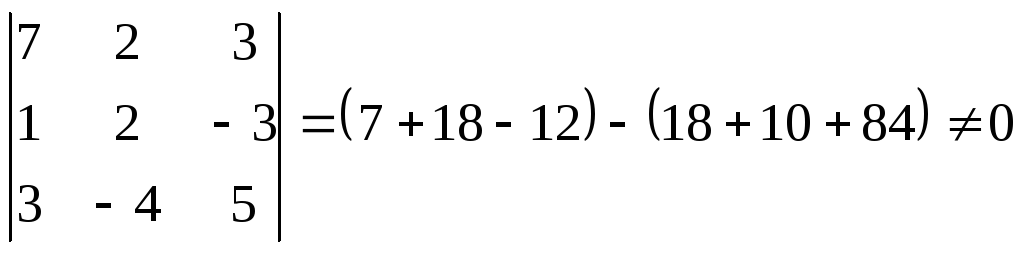линейно не зависима.

5. Разложить вектор по векторам

Решение.

Составим матрицу из координат данных векторов.

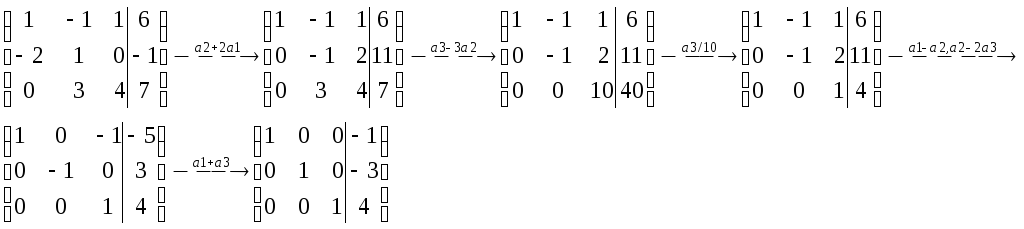
Ответ:

6. Найти собственные числа матрицы .

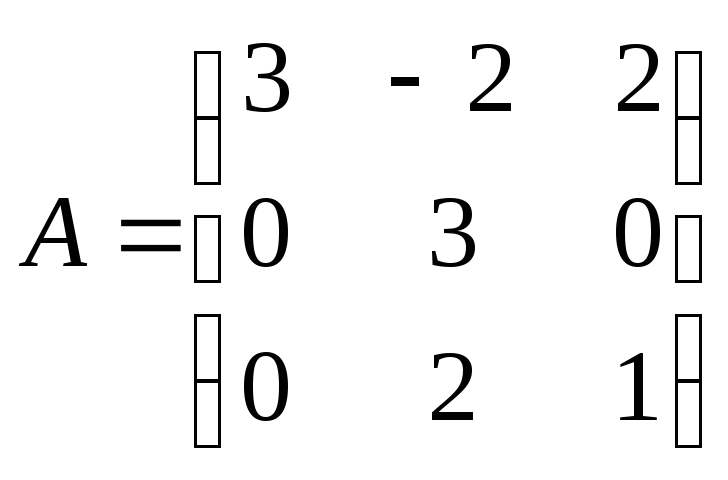Решение.

Характеристическими числами линейного преобразования матрицы служат действительные корни уравнения ой степени, которое можно записать в виде .

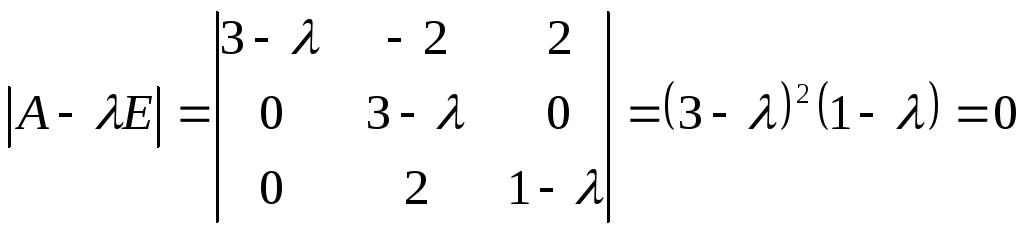
Ответ: собственные числа матрицы .

7. Найти фундаментальные решение системы

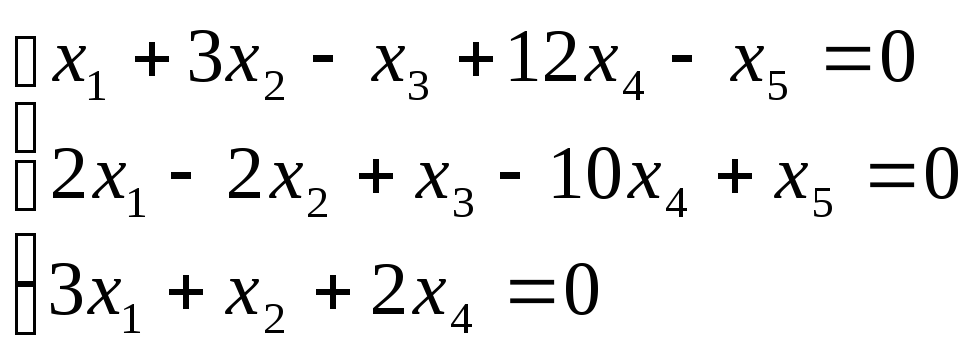
Решение.

Составим матрицу

Пусть , тогда

Ответ:

2. Решить систему методом Гаусса

а)

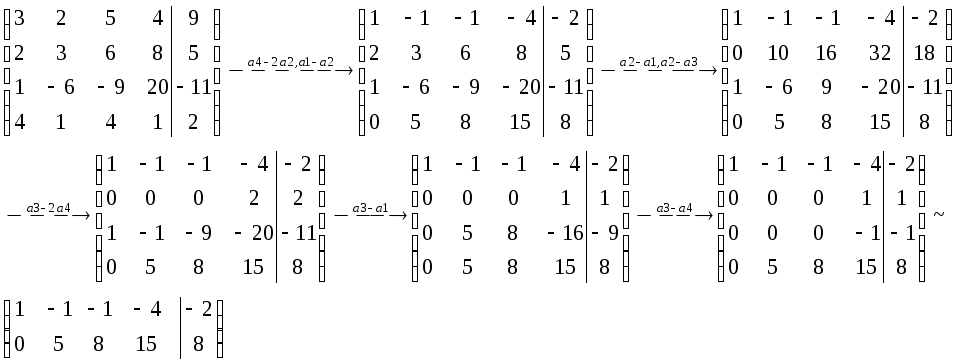
Пусть

б)

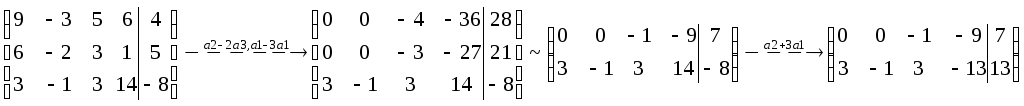
пусть тогда

Ответ: где

в) не имеет решения

г)