Отчет по учебной практике

Министерство образования Российской Федерации

Удмуртский государственный университет

Математический факультет

Кафедра математического анализа

ОТЧЕТ ПО УЧЕБНОЙ ПРАКТИКЕ

Тема работы:

" Обращение матриц и вычисление определителя по схеме Гаусса "

Научный руководитель:

Исполнитель: студент группы 11–23, Захарова Валентина Михайловна

Ижевск 2007

Введение

Современная вычислительная техника требует от инженеров и техников знаний основ вычислительной математики и применения этих знаний к решению различных практических задач.

Вычислительная математика являлась и является одной из основных дисциплин, необходимых для подготовки специалистов, работающих в различных областях.

Кому как не нам, прикладным математикам, заниматься решением этих задач!

В данном отчёте представлена работа по решению задач, связанных с обращением матриц и вычислением определителя по схеме Гаусса.

Сама задача состоит в том, чтобы найти обратную матрицу и найти её определитель.

Задание

Каждый студент сам выбрал себе задание. Меня привлекает работа с матрицами, я иду на кафедру алгебры, поэтому я взяла задание из темы "Алгебра матриц.Обращение матрицы и вычисление определителя по схеме Гаусса".

Задание № 16.

Обращение матрицы и вычисление определителя по схеме Гаусса.

Обратить матрицу и вычислить её определитель по схеме Гаусса с точностью до

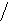
Подпись руководителя практики:

Для решения данной задачи я определила для себя следующие этапы:

1. Общие способы нахождения обратной матрицы. Их описания.

2. Описание метода Гаусса для нахождения определителя.

3. Выбор метода для нахождения обратной матрицы.

4. Алгоритм решения общей задачи.

5. Программа на языке Pascal для общего случая (по алгоритму).

6. Правильность программы на примерах.

7. Результаты (5. для данной задачи).

8. Преимущества программы, написанной на Pascal, над решением "вручную".

Способы нахождения обратной матрицы{1}

Определение. Пусть матрица А. Матрица называется обратной к матрице А, если выполнено соотношение:

А*=*А=Е,

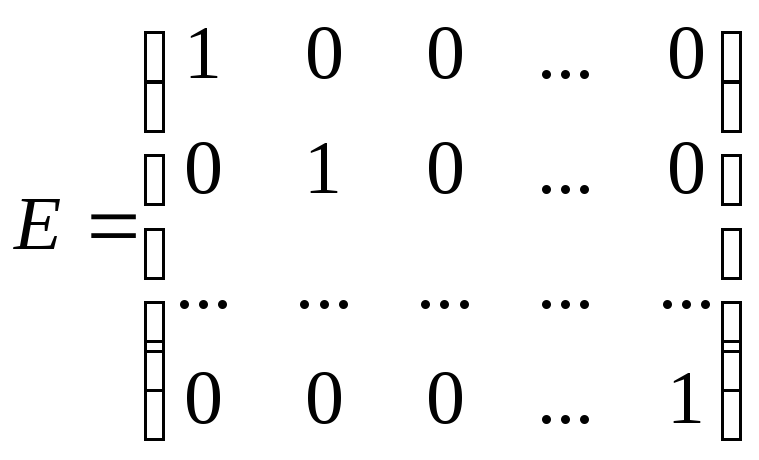
где Е=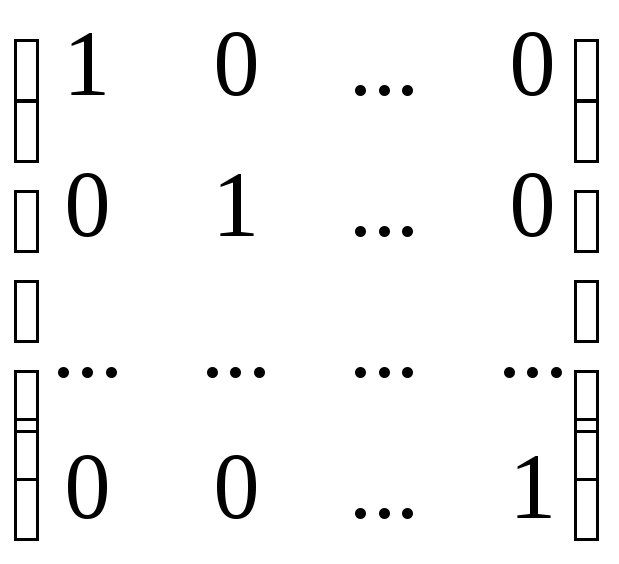 – единичная матрица,– множество квадратных матриц ( размерами n на n ) над полем К.

Обратные матрицы позволяют решать матричные уравнения вида:

,

A,B. Если detA0, то

.

1. Обратная матрица для данной неособенной матрицы находится по формуле

=,

где detA – определитель матрицы А; – алгебраические дополнения соответствующих элементов матрицы А.

2. Формулы для обращения клеточной матрицы

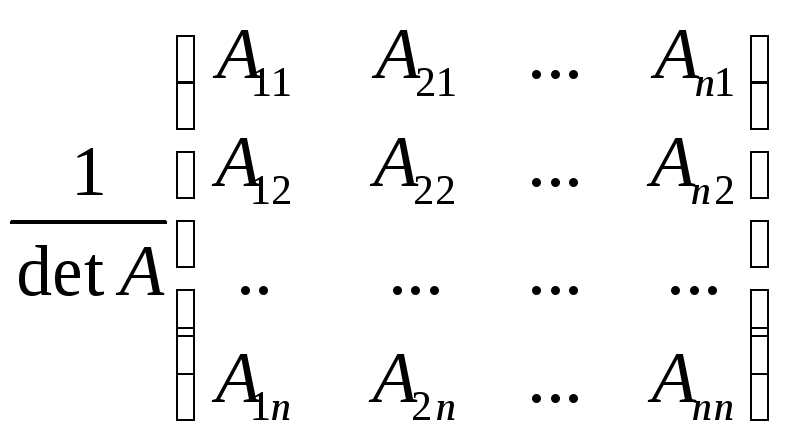
S=.

Обратная матрица ищется в виде клеточной матрицы

.

а) Если легко определяется матрица , то –, , –, .

б) Если легко определяется матрица , то , , –, .

3. Обращение матриц методом окаймления. Пусть

,

где – столбец, – строка, – число. Обратная матрица ищется в виде

,

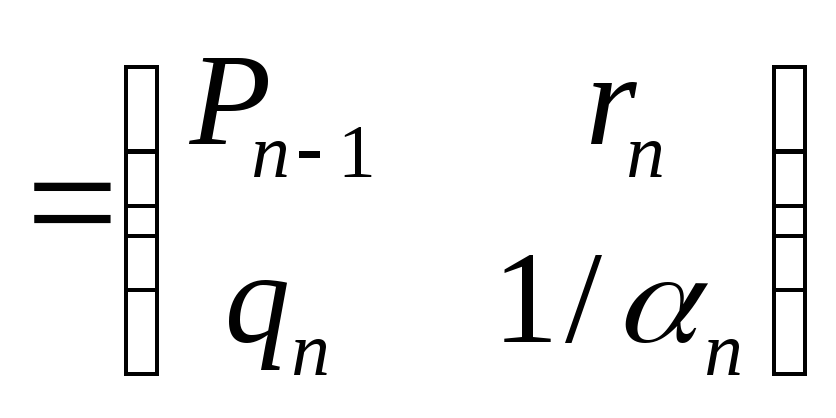где ; ; ; .

4. Обращение матрицы с помощью разбиения её на произведение двух треугольных матриц. Пусть

, где ; .

Обратная матрица ищется в виде .

5. Для нахождения обратной матрицы к А составляем расширенную матрицу (), и, преобразованием только строк, получаем из (АЕ) расширенную матрицу () ( для работы со столбцами надо рассмотреть ).

Определитель{2}

Определение. Определителем матрицы А=(), K– поле, называется число, которое вычисляется по правилу:

detA=A==, где и число инверсий индексов строк и столбцов соответственно.

Есть много способов нахождения определителей. Мы рассмотрим лишь один из них.

Метод Гаусса заключается в том, что мы приводим определитель к треугольному виду, а затем перемножаем элементы, стоящие на главной диагонали.

Пусть дана матрица .

={ для }=

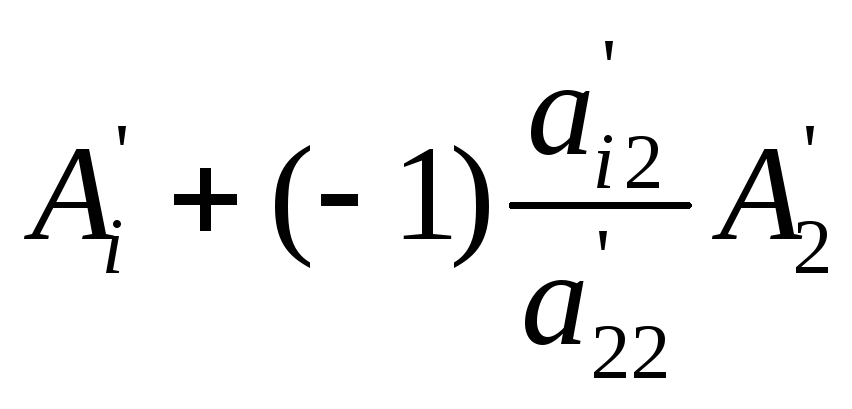=={ для }= ==…==.

Этот метод реализован в процедуре Opredelitel_Obratn_Matrix программы "Обратная матрица и её определитель ". Несмотря на то, что процедура носит название как "Определитель обратной матрицы" её можно использовать для произвольной матрицы.

Выбор метода. Алгоритм.{3,4}

Я выбрала пятый метод, так как я с ним уже знакома.

Рассмотрим его более подробно.

; ;

( преобразования строк)

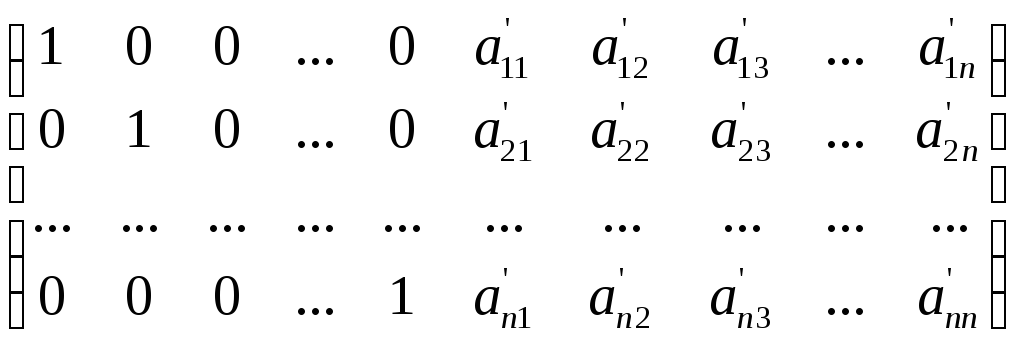=(E), где ; (A) и ().

Поле К в нашем случае– поле вещественных чисел().

Как преобразовать строки?

Умножим первую строку на (0 ). Заметим, что первый элемент первой сроки стал равен единице. С помощью этой еденицы "обнуляем" первый столбец, начиная со второй строки ( для ). Для этого первую строку умножаем на элемент () и вычитаем из соответствующей i–ой строки.

()=

==(*)

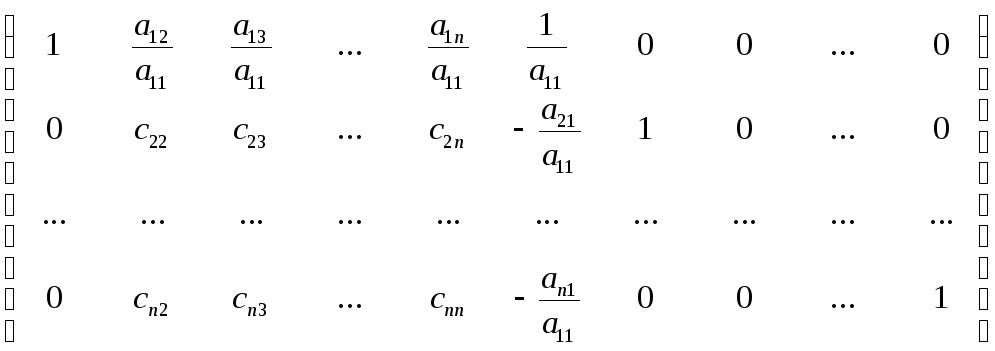{ где для }

Умножим вторую строку на (0 ). Заметим, что второй элемент второй строки стал равен единице. Теперь с помощью этой еденицы "обнуляем" второй столбец, начиная с третьей строки .Для этого вторую строку умножаем на элемент () и вычитаем её из соответствующей i–ой строки.

Далее аналогично проделываем это еще (n–3) раза. В (n–2)–ой раз остаётся лишь поделить "n"–ую строку на "nn"–ый элемент.В результате получаем матрицу вида:

(*)=(SB)

Мы действовали "сверху–вниз".

Аналогично действуем "снизу–вверх". Отличие в том, что теперь не надо умножать строки на элементы, так как единицы уже получены и стоят они на главной диагонали матрицы S.

В итоге должны получить матрицу вида:

(SB)=().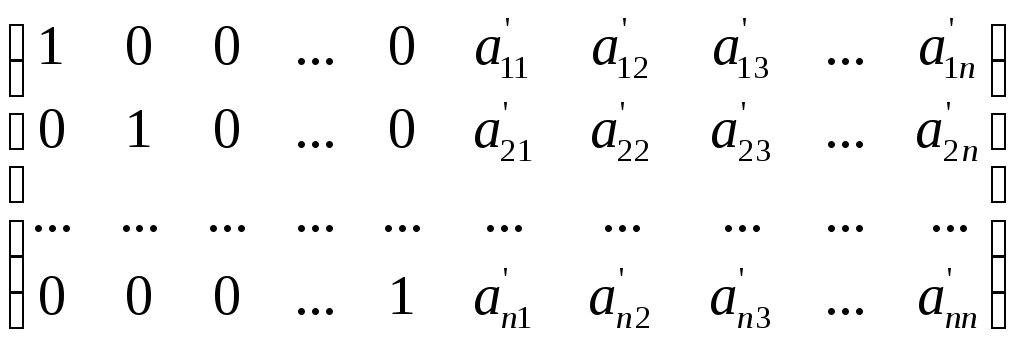

В процедуре Obratn_matrix программы "Обратная матрица и её определитель ", написанная на языке Pascal, реализовывается именно этот способ нахождения обратной матрицы.

Программа "Обратная матрица и её определитель "{5}

PROGRAM OBR_MATRIX_EE_OPREDELITEL;

Uses Crt;

Const n=4; {Размер матрицы}

Type Matrix=array[1..n] of array[1..n] of extended;

RashMatrix=array[1..n] of array[1..2*n] of extended;

{чтобы активизировать тип extended: options->compiler->8087/80287(поставить X)}

VAR i,j,k,kk:word; { вспомогательные величины}

A,E,OB:Matrix; {величины для обозначения данной матрицы, еденичной и обратной соответственно}

AE:RashMatrix; { величина для обозначения расширенной матрицы }

Del,Opredelitel: extended; {вспомогательная величина,величина для обозначения определителя }

PROCEDURE Print_matrix( var A: Matrix ); {Вывод матрицы на экран}

begin

For i:=1 to n do

begin

For j:=1 to n do

If A[i,j]>=0 then

write(' ',(Trunc(A[i,j])+round(frac(A[i,j])*10000)*0.0001):4:4, ' ' )

else

write((Trunc(A[i,j])+round(frac(A[i,j])*10000)*0.0001):4:4, ' ' );

writeln;

end;

end;

PROCEDURE Opredelitel_Obratn_Matrix(OB: Matrix;Opredelitel:extended); {Определитель обратной матрицы}

Begin

Opredelitel:=OB[1,1];

k:=1;

While k<=n-1 do

Begin

Del:=OB[k,k];

For j:=k to n do OB[k,j]:=OB[k,j]/Del;

For i:=k to n do Begin

For j:=1 to n do OB[i,j]:=OB[i,j]-OB[k,j]*OB[i,k];

End;

Opredelitel:=Opredelitel*OB[k+1,k+1];

k:=k+1;

End;

write('определитель обратной матрицы равен ', (Trunc(Opredelitel)+round(frac(Opredelitel)*10000)*0.0001):4:4)

End;

PROCEDURE Obratn_matrix(A,E,OB: Matrix;AE:RashMatrix);

{Обратная матрица, вывод её на экран, вывод на экран её определителя}

Begin

{Составляем еденичную матрицу}

For i:=1 to n do

For j:=1 to n do

If j=i then E[i,j]:=1

else E[i,j]:=0;

{Составляем расширенную матрицу}

For i:=1 to n do

For j:=1 to 2*n do

If j<=n then AE[i,j]:=A[i,j]

else AE[i,j]:=E[i,j-n];

{Преобразования расширенной матрицы}

k:=1;

While k<=n do

Begin

Del:=AE[k,k];

For j:=k to 2*n do AE[k,j]:= AE[k,j]/Del;

For i:=k+1 to n do

For j:=1 to 2*n do AE[i,j]:=AE[i,j]-AE[k,j]*A[i,k];

k:=k+1;

End;

kk:=n;

While kk>0 do

Begin

For i:=kk downto 1 do

For j:=1 to 2*n do

AE[i,j]:=AE[i,j]-AE[kk,j]*AE[i,kk];

kk:=kk-1;

end;

For i:=1 to n do

For j:=1 to n do

OB[i,j]:=AE[i,j+n];

writeln;

Print_Matrix(OB);{Для вывода обратной матрицы}

Opredelitel_Obratn_Matrix(OB,Opredelitel)

End;

{тело программы}

BEGIN

ClrScr;

For i:=1 to n do

For j:=1 to n do

begin

writeln ('введите элемент',i,'-ой строки ', j,'-го столбца' );

readln (A[i,j]);

end;

writeln (' данная матрица ');

print_matrix(A);

writeln;

write('обратная матрица');

Obratn_matrix(A,E,OB,AE);

END.

Примечание 1. В программе для вывода на экран матрицы и определителя используются функции Trunc, round, frac. Функция Trunc отсекает дробную часть вещественного числа, оставляя длинное целое. Round преобразует вещественное значение в ближайшее к нему значение типа LongInt. Frac– дробная часть вещественного числа, так же имеющие вещественный тип.

Примечание 2. В данной программе не рассматриваются случаи, когда необходимо поменять местами строки ( например, первый элемент матрицы равен нулю ). Но это можно осуществить следующим образом: ввести переменные ind:word и Ctroka: array[1..2*n] of extended (ind–вспомогательный элемент, Ctroka– для обозначения строки, которую будем менять с той строкой, у которой на главной диагонали первой "полуматрицы" расширенной матрицы стоит 0) ; в процедуре Obratn_matrix перед преобразованием расширенной матрицы вставить (не забыв провести соответствующего наращивания индекса ind :

If AE[ind,k]=0 then

Begin

ind:=ind+1;

For j:=1 to 2*n do

Ctroka[j]:=Ae[ind,j];

For j:=1 to 2*n do

AE[ind,j]:=AE[k,j];

For j:=1 to 2*n do

AE[k,j]:=Ctroka[j];

End;

Простейшие примеры для отладки и тестирования программы{6}

Пример 1.В программе в разделе констант n приравниваем двум и запускаем прграмму ( Ctrl+F9).

На запрос программы вводим элементы матрицы . После нажатия Alt+F5 мы увидим на экране:

Пример 2. В программе в разделе констант n приравниваем трём и запускаем прграмму ( Ctrl+F9).

На запрос программы вводим элементы матрицы 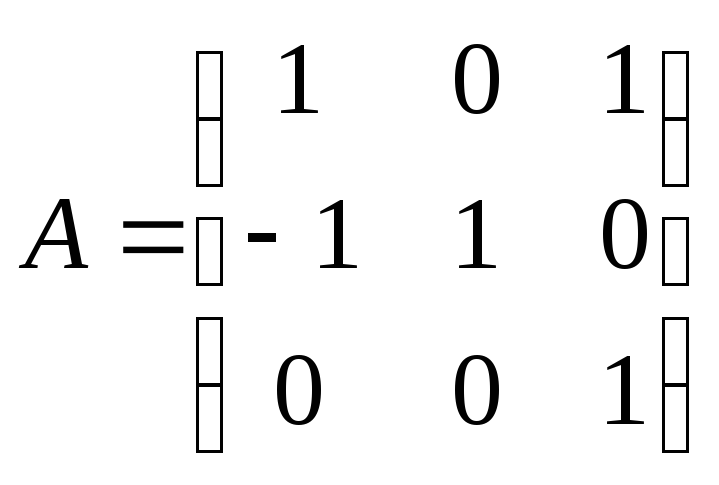. После нажатия Alt+F5 мы увидим на экране:

Легко проверить, что обратные матрицы действительно являются обратными к данным (по определению). Да и определители можно посчитать вручную.

Выполнение задачи №16 в Тurbo Pascal. {7}

Запускаем программу"Обратная матрица и её определитель " (Сtrl+F9); вводим с клавиатуры элементы матрицы (на соответствующий запрос программы).

– данная матрица (“matrix” на экране);

Программа работает считанные доли секунды. Вообщем, очень быстро ( в отличие от метода вручную или с помощью калькулятора).

Нажав сочетание клавиш Alt+F5 получаем:

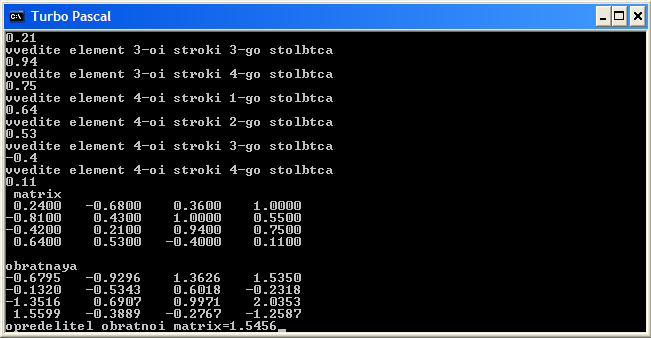
Таким образом, обратная матрица , а её определитель det=1,5456. Заметим, что обратная матрица выводится на экран так же с точностью , как и определитель.

Преимущества программы{8}

• Скорость работы.

• Диалоговый режим.

• Подходит для матриц любого размера ( ограничено лишь памятью).

• Многие знают язык Pascal, разобраться в программе можно за короткий срок.

• Вывод данных в понятном виде.

Минусы программы заключены в её плюсах: простой язык (Turbo Pascal),ограничение памяти. Конечно программа не может сравниться с программами, написанными на других, более современных, языках. В первую очередь, она помогла мне закрепить навыки программирования. Подобные задачи помогают развивать в себе не просто математика, а именно прикладного математика. Наверняка, подобные задачи разобраны в таких пакетах как Mathematica, Maple и др.

Общие выводы

Данный отчет был подготовлен в течение нескольких дней. Большую часть времени заняло составление программы на языке Turbo Pascal. Результаты работы меня удовлетворили. Я более чётко определила для себя правила составления отчета, в чем сильно помогли методические указания и рекомендации по вычислительной практике (автор Латыпова Н.В.). Так же я вспомнила некоторые возможности Turbo Pascal ( например, использование процедур). Просмотрела полезные книжки и лекции, которые помогли подготовить отчет (Воробьёва Г.Н., Данилова А.Н. "Практикум по вычислительной математике";

Немнюгин С.А."Turbo Pascal. Программирование на языке высокого уровня";Лекции по алгебре( Читал Мерзляков А.С.)). Разобрала новые, для меня, возможности пакета Mathematica ( использование матриц ).

Список литературы

• Латыпова Н.В./Методические указания и рекомендации по вычислительной практике/УдГУ. Ижевск, 2004.16с.

• Воробьёва Г.Н., Данилова А.Н./ Практикум по вычислительной математике./Высш. Шк.,1990.

• Немнюгин С.А./ Turbo Pascal. Программирование на языке высокого уровня/ учебник для вузов. 2–е изд– СПб, 2005.

• Лекции по алгебре. Читал Мерзляков А. С.

Аннотация

Данный отчет на тему обращение матриц и вычисление определителя по схеме Гаусса содержит в себе:

• Введение

• Задание и его описание

• Этапы решения задания

• Описание каждого из этапов (включая методы решения, алгоритмы, компьютерную программу, примеры тестирования)

• Общие выводы о проделанной работе

• Список литературы

• Дискета с отчетом и программой на языке Turbo Pascal