
- •Вопрос 1: Электрическая цепь и ее элементы.
- •Вопрос №2: Величины электрических цепей.
- •Вопрос №3: Линейные и нелинейные электрические цепи.
- •Вопрос №4: Источники электрической энергии.
- •Вопрос №5: Приемники электрической энергии.
- •Вопрос №6: Основные топологические понятия и выражения.
- •Вопрос №7: Законы Ома и Кирхгоффа.
- •Вопрос №8:Понятия об установившемся и переходном процессе. Законы коммутации.
- •Вопрос №9: Анализ линейных цепей с применением законов Кирхгоффа. Пример.
- •Вопрос №11: Анализ методом контурных токов (мкт). Пример.
- •Вопрос №12: Метод междуузлового напряжения. Пример.
- •Вопрос №13: Параметры синусоидального тока (напряжения).
- •Вопрос №14: Векторная форма представления синусоидальных величин.
- •Вопрос №15: Комплексное представление синусоидального тока (напряжения).
Вопрос №9: Анализ линейных цепей с применением законов Кирхгоффа. Пример.
При анализе электрических цепей определяют значение токов в их ветвях, падение напряжения на элементах или потребляемую мощность по заданному значению Э.Д.С., а также значение сопротивлений, проводимостей или других параметров по заданным значениям тока или напряжения. Для определенности будем полагать, что расчету подлежит значение токов ветвей схемы. Применяется при нескольких ЭДС в цепи. Суть анализа электрических цепей применением законов Кирхгофа заключается в составлении системы из N независимых линейных уравнений, где n – число сложных узлов, k – число независимых контуров: N = (n-1) + k. По I закону Кирхгоффа составляется (n-1) – число уравнений; По II закону Кирхгоффа составляют k-уравнений.
П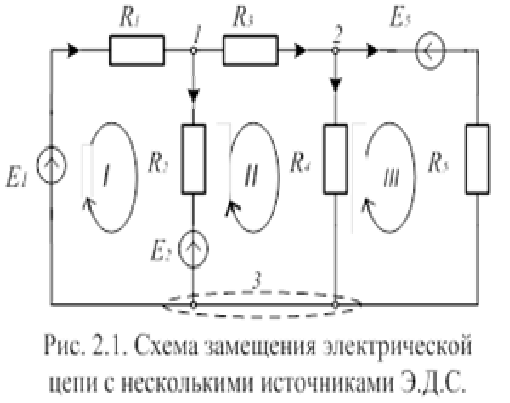 ример:
дано: E1,
Е2,
E5,
R1
– R5.
Определить: токи в ветвях.
ример:
дано: E1,
Е2,
E5,
R1
– R5.
Определить: токи в ветвях.
Решение: 1. Произвольно отмечаем токи в системе: I1 – I5.
2. Определяем количество контуров: k = 3 и задаем направление контуров. В системе 3 сложных узла: n = 3.
3. Составляем уравнения по I закону Кирхгоффа: n – 1 = 2.
Узел 1: I1 – I2 – I3 = 0;
Узел 2: I3 – I4 – I5 = 0.
Составляем уравнения по II закону Кирхгоффа: k = 3.
Контур I: I1*R1 + I2*R2 = E1 – E2;
Контур II: I3*R3 + I4*R4 – I2*R2 = E2;
Контур III: I5*R5 – I4*R4 = - E5.
Подставляем значения E и R в уравнения.
Примечание: Если при решении какой-либо ток получился отрицательным, то нужно в схеме изменить его направление на противоположное (нарисовать стрелку рядом). Для проверки правильности решения составляется уравнение баланса мощностей: при P = U*I = I2*R.
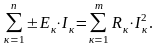
Примечание: знак «+» ставится в первой части равенства, если направление тока и ЭДС совпадают.
Вопрос №10: Анализ электрических цепей методом эквивалентных преобразований. Пример.
К![]() огда
в состав электрической цепи входит
только один источник Э.Д.С., его ток
определяется общим сопротивлением
пассивных приемников электрической
энергии. Такое сопротивление называют
эквивалентным – Rэкв.
Очевидно, что если известно Rэкв,
то цепь можно представить в виде двух
последовательно соединенных элементов
– источника Э.Д.С. и Rэкв,
а определение тока источника сводится
к применению закона Ома. Процесс перехода
от электрической цепи с произвольной
топологией к цепи с Rэкв
называется эквивалентным
преобразованием.
Приемы преобразования электрической
цепи определяются способами соединения
пассивных элементов. Различают четыре
основных способа соединения:
последовательное,
параллельное, треугольником и звездой.
Рассмотрим сущность эквивалентных
преобразований при каждом из названных
способов.
огда
в состав электрической цепи входит
только один источник Э.Д.С., его ток
определяется общим сопротивлением
пассивных приемников электрической
энергии. Такое сопротивление называют
эквивалентным – Rэкв.
Очевидно, что если известно Rэкв,
то цепь можно представить в виде двух
последовательно соединенных элементов
– источника Э.Д.С. и Rэкв,
а определение тока источника сводится
к применению закона Ома. Процесс перехода
от электрической цепи с произвольной
топологией к цепи с Rэкв
называется эквивалентным
преобразованием.
Приемы преобразования электрической
цепи определяются способами соединения
пассивных элементов. Различают четыре
основных способа соединения:
последовательное,
параллельное, треугольником и звездой.
Рассмотрим сущность эквивалентных
преобразований при каждом из названных
способов.
Последовательное соединение элементов:
Характеризуется одним и тем же значением силы тока. Согласно второму закону Кирхгофа, можно записать: I*R1 + I*R2 + … + I*Rn = I*Rэкв., откуда Rэкв. = R1 + R2 + … + Rn, а I = U/Rэкв. Таким образом, видим, что схема из n последовательно соединенных резистивных элементов может быть заменена схемой с одним элементом.
П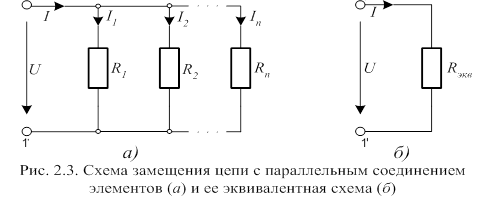
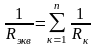 араллельное
соединение элементов:
Параллельным называют соединение, при
котором все элементы цепи присоединяются
к двум сложным потенциальным узлам и
находятся под воздействием одного и
того же напряжения. Схема такой цепи
приведена на рис. 2.3. Ток каждой к
– ой ветви этой цепи определяется
напряжением источника U
и проводимостью Gk
соответствующей ветви: Ik
= Gk*U.
Определим правило эквивалентной замены
разветвленной схемы рис.2.3, а на простейшую
схему рис 2.3, б. Условием эквивалентности
схем является равенство токов на зажимах
1 – 1′, т. е.: I
= I1
+
I2
+ … + In.
Подставляя
значение токов, получим: U/Rэкв.
= U/R1
+
U/R2
+… + U/Rn,
откуда
или в единицах проводимости:
араллельное
соединение элементов:
Параллельным называют соединение, при
котором все элементы цепи присоединяются
к двум сложным потенциальным узлам и
находятся под воздействием одного и
того же напряжения. Схема такой цепи
приведена на рис. 2.3. Ток каждой к
– ой ветви этой цепи определяется
напряжением источника U
и проводимостью Gk
соответствующей ветви: Ik
= Gk*U.
Определим правило эквивалентной замены
разветвленной схемы рис.2.3, а на простейшую
схему рис 2.3, б. Условием эквивалентности
схем является равенство токов на зажимах
1 – 1′, т. е.: I
= I1
+
I2
+ … + In.
Подставляя
значение токов, получим: U/Rэкв.
= U/R1
+
U/R2
+… + U/Rn,
откуда
или в единицах проводимости:
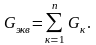
Таким образом, цепь, состоящая из n параллельных резистивных элементов, может быть заменена простейшей цепью, эквивалентное сопротивление которой определяется выражением. При параллельном соединении двух резистивных элементов с сопротивлениями R1 и R2 их эквивалентное сопротивление равно: Rэкв. = (R1*R2)/(R1+R2), а эквивалентная проводимость:
Gэкв. = 1/R1 + 1/R2 = (R1+R2)/(R1*R2) = G1 + G2. Токи двух ветвей при их параллельном соединении определяются по правилу деления токов: I1 = I*(U/R1) = I*(Rэкв./R1) = I*(R2/ R1+R2); I2 = I*(R1/ R1+R2).
С оединение
элементов звездой или треугольником:
Соединение
трех сопротивлений в виде трехлучевой
звезды (рис. 2.4, а), называют соединением
«звезда», а соединение, при котором
элементы образуют стороны треугольника
(рис. 2.4, б), – «треугольник».
оединение
элементов звездой или треугольником:
Соединение
трех сопротивлений в виде трехлучевой
звезды (рис. 2.4, а), называют соединением
«звезда», а соединение, при котором
элементы образуют стороны треугольника
(рис. 2.4, б), – «треугольник».
О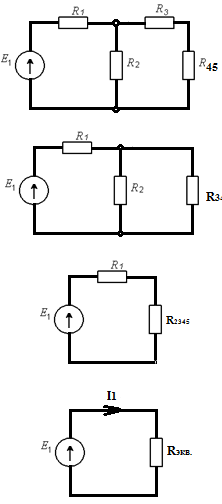 чень
часто при расчете электрических цепей
оказывается целесообразным преобразовать
треугольник в звезду. При преобразовании
треугольника в звезду следует пользоваться
выражениями:
чень
часто при расчете электрических цепей
оказывается целесообразным преобразовать
треугольник в звезду. При преобразовании
треугольника в звезду следует пользоваться
выражениями:
R1 = R12*R13/(R12 + R23 + R13); R2 = R12*R23/(R12 + R23 + R13); R3 = R13*R23/(R12 + R23 + R13).
При преобразовании звезды в треугольник следует пользоваться выражениями:
R12 = R1 + R2 + (R1*R2)/R3; R23 = R2 + R3 + (R2*R3)/R1; R13 = R1 + R3 + (R1*R3)/R2.
П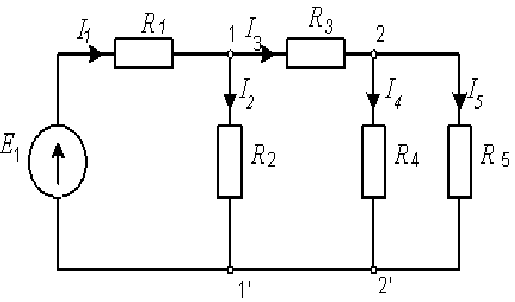 ример:
Дано: E,
R1
– R5;
ример:
Дано: E,
R1
– R5;
Определить: токи в ветвях I1 – I5.
Решение: 1. Находим параллельные соединения:
R45 = (R4*R5)/(R4+R5).
2. Находим последовательное соединение: R345 = R3 + R45
3. R2345 = (R2*R345)/(R2+R345);
4. Rобщ. = Rэкв. = R1 + R2345.
5. Преобразуем в простую схему: I1 = E/Rэкв.; U13 = E – I1*R1;
I2 = U13/R2; По I закону Кирхгоффа: I3 = I1 – I2.
