1. Числовая последовательность. Пусть N – множество натур чисел. Если каждому натур числу n поставлено в соответствие некоторое число x_n, то говорят, что определена числовая последовательность х₁, х₂,…, х_n. Числа х_nназыв элементарными или членами последовательности. Числовую последовательность будем записывать в виде {x_n}. Последовательности {x_n+y_n}, {x_n-y_n}, {x_ny_n}, 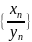назыв соответственно суммой, разностью, произведением и частным двух последовательностей {x_n} и {y_n}. Последовательность {x_n} назывограниченной, если существуем М>0 такое, что для любого nϵN: 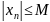. Последовательность {x_n} назывнеограниченной, если для любого М>0 существует nϵN: .

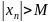2. Понятие функции. График функции. Пусть Х и У-два произв. множества действ.чисел,если каждому элементу х из множ.Х по некорот. правилу f поставлен в соотв. вполне опред.эл-т у из множ.У ,то –задана функция f и исп.след.обозн. y=f(x). переменная х наз. независимой переменной или аргументом ф-ции, переменная у-зависимая переменная или ф-ция. Ф-ция,все значения кот. равны м\у собой наз.посмтоянной и обозн.С. Ф-цияf,определенная на множ.Хназ.ограниченной, если сущ.М>0,такое что все х из множ.Х: |f(x)|<=M. Ф.f(x)наз. возрастающей(убыв.)на множ.Х,если для люб.знач.х1 и х2 ,таких ,что х2>х1,из этого множ.выполн.нер-во: f(x2)>f(x1) (f(x2)<f(x1)).Если для люб. х2>х1 выполн. f(x2)>=f(x1)( f(x2)<=f(x1)),то ф. наз.неубыв.(невозр.). Данные ф-цииназ.монотонные. Графиком ф-ции наз. множ.всех точен плоскости с корд. (х, f(x)),т.е. корд. х и у связаны соотнош. y=f(x).

3.Предел последовательности. Св-ва сходящихся послед-тей. Число а наз. пределом послед-сти {x_n}, если для любого ɛ>0 сущ. 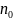из n € N,такое что для люб n> выполн. неравенство 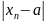<ɛ и обозн. а= .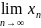

Геометрически это обозн.,что в любой ɛ -окресности точки а находятся все члены послеловательности начиная с некоторого номера n (зависит от ɛ).Опр. Послед-ть, имеющая конечный предел наз. сходящейся, а посл-ть не имеющая предела – расходящейся.Опр.Посл-ть{x_n} наз. бесконечно малой, если ее предел равен нулю.Свойства сходящихся последовательностей:1)Для того,чтобы число а было пределом последовательности необходимо и достаточно,чтобы имело вид =а+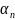 , где - б.м.п.

2)Сходящ. Послед.Имеет только 1 предел

3)Сходящ. Послед.Ограничена

4)Пусть =a и 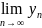=b, тогда

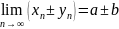
(b )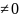

4. Предел функции в точке. Односторонние пределы.Число b наз. пределом функции f в точке х=а(или при х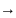 а), если для любой последовательности {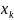 }, сходящейся к а, соответствующая последовательность значений функции { f(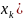 } сходится к b.

Для обозначения функции f в точке х=а используется запись 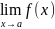=b – определение предела функции по Гейне.

Односторонние пределы

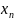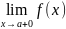Число b наз. правым пределом в точке х=а, если для любой сходящейся к а последовательности { }, члены кот.больше или равны а, соответствующая последовательность { f( } сходится к b, обозначается: =b.

Число b наз. левым пределом в точке х=а, если для любой сходящейся к а последовательности { }, члены кот.меньше или равны а, соответствующая последовательность { f( } сходится к b, обозначается: =b. правый и левый предел функции в точке наз. односторонними. В случае, когда а=0, исп. Обозначение: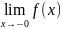 , 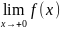. Очевидно, если сущ-ет =b, то сущ-ет и оба односторонних предела, причём b совпадает с ними.

Справедливо и обратное утверждение: если сущ-ют оба односторонних предела и они равны, то сущ-ет предел =b и при этом b= f(a-0)= f(a+0) . Если же односторонние пределы не равны, т.е. f(a-0)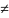 f(a+0), то и предел не сущ-ет.

5. Предел ф-ции при X . Св-ва предела ф-ции.

Число bназ.пределомf(x) при x-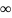 если для любой бесконеч.большой последоват.Хn соответствующ . последовател.знач.ф-ции f{(хn)} сходятся к b и обознач.limf(х)=b.Ф-ция наз.бесконеч.малой при х-а асли предел limf(х)=0.Ф-ция наз.бесконеч. большой при х-а,еслиlimf(х)= .Св-ва:1)Предел (сум./раз.)= (сумб/раз) пределаlim(f(х)+-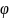 (х)= limf(х)+-lim (х).След-е1 Ф-ция может иметь только 1 предел в т.х=а.2)предел произвед.2-х ф-ций=произвед.их пределов lim(f(х)* (х))=lim

f(х)*lim (х).След-е2 а)постоян . множитель можно вынасить за знак предела.б)предел степени с натурал.показателем=той же степени предела.3)предел дроби=пределу чеслителя деленному на предел знаменат.,если предел знамен.не равен 0. limf(х)/ (х)= f(х)/lim (х). Прав.Лопиталя-м-д нахождения пределов ф-ий, раскрывающий неопределённости вида0/0 и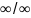 . Обосновывающая м-д теорема утверждает, что при некоторых усл. предел отношения ф-ий =пределу отношения их производных.

6. Непрерывность функции. Пусть ф.f(x) определена в некоторой окрестности точки x=a. Ф-ция f(x) назыв непрерывной в точке а, если 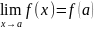(1). Равенство (1) означает выполнение трёх условий: 1. Ф. f(x) определена в точке х=а и в некоторой её окрестности; 2. Ф. f(x) имеет предел при х→а; 3. Предел ф-ии f(x) в точке а равен значению ф-ии в этой точке. Т.к. 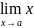=а, то рав-во (1) можно записать в виде 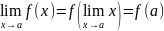. Это означает, что при нахождении предела непрерывной ф. f(x) можно перейти к пределу под знаком ф-ии, т.е. в ф-ию f(x) вместо аргумента х можно подставить его предельное значение.Опр. Если 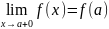, то ф. f(x) наз. непрерывной в точке а справа, если , то- непрерывной в точке а слева. Для того, чтобы функция f(x) была непрерывной в точке а, необходимо и достаточно чтобы она была непрерывной в этой точке слева и справа. Приведём ещё одно определение функции, непрерывной в точке а. Равенство (1) равносильно: 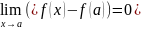. если учесть, что соотношения х→а и (х-а)→0 также равносильны, то получим, что условие непрерывности ф. f(x) в точке а записывается в виде 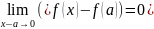(2) . опр. Разность х-а назывприрощением независимой переменной х в точке а и обозначают через Δх, Δх=х-а, а разность f(x)-f(a) – приращением функции f(x) в точке а и обозначают Δy=f(x)-f(а).теперь условие (2) можно записать: (3). Заметим здесь, что х=а +Δх и f(a+Δх)=f(a)+Δy. Тогда новое определение непрерывности функции: ф. f(x) назыв непрерывной в точке а, если её приращение в этой точке есть бесконечно малая функция.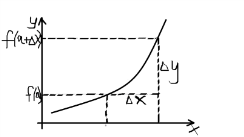

Опр. Ф. f(x) назыв непрерывной на интервале (а;в), если она непрерывна в каждой точке хϵ(а;в). Если же, кроме того, функция f(x) непрерывна в точке а слева, а в точке в – справа, то функция f(x) назыв непрерывной на отрезке [a;в]. Опр. Ф. f(x) назыв кусочно-непрерывной на отрезке [a;в], если она непрерывна во всех внутренних точках [a;в], за исключением конечного числа точек, в которых она имеет разрывы первого рода, а в точках а и в имеет соответствующие односторонние пределы

8. Понятие производной ф-ции. Геом. смысл производной.пусть функция y=f(x) определена и непрерывна в окрестности точки x=a. если независимой переменной x придать приращения ∆x в этой точке, то функция получит приращение ∆y=f(a+∆x)-f(a). Если приращение ∆x→0 то определению непрерывной в точке x=a функции ∆y→0. С целью исследования скорости изменения значений функции вводится понятие производной и определение – производная функция y=f(x) в точке x=a- предел отношения приращения функции в точке x=a к приращению аргумента если ∆x→0.обозначают f'(a), y'(a). Согласно определению 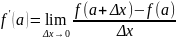(1) операция нахождения производной – дифференцирование. Теорема: если функция y=f(x) в точке x имеет производную, то она непрерывна в этой точке.

Геометрический смысл: пусть y=f(x) определена на интервале (a;b) и пусть кривая AB-график этой функции. Пусть точка М (x₀;f(x₀))-произвольная точка графика. Придадим аргументу x₀ приращение ∆x. Соответствующую точку на графике обозначим через Р(x₀+∆x ;f(x₀+∆x)). Через точки М и Р построим секущую.найдём угловой коэффициент секущей. Понятно, что k=tg NMP=∆f/∆x. если точку Р устремить по кривой к точке М то положение секущей МР будет изменяться. Если ∆x→0 и существует предельное положение секущей, то полученная прямая называется касательной к графику функции y=f(x) в точке x₀. Понятно, сто условием существования предельного положения секущей является существование предела k_кас=LimΔx→0∆f/∆x=LimΔx→0k_∆x=f'(x₀) график функции имеет касательную в точке x₀ тогда и только тогда, когда функция дифференцируема в этой точке и f'(x₀)-угловой коэффициент касательной. Тогда уравнение касательной в точке М₀(x₀;y₀) – y-y₀= f'(x₀)(x-x₀) (2) прямая проходящая через точку (x₀;y₀) и перпендикулярная касательной – нормаль к графику функции, и учитывая условия перпендикулярности двух прямых и формулу(2) имеет вид: y-y₀=(-1/ f'(x₀))* (x-x₀) если f'(x₀)=0, то уравнение нормали: x=x₀

7. Точки разрыва ф-ции. точка а – точка разрыва f(x) если f(x) не является непрерывной в этой точке.если x=a – точка разрыва y=f(x) то в ней не выполняется по крайней мере одно из условий 1-ого определения непрерывности функции а именно:1. Функция определена в некоторой окрестности точки а, но не определена в самой точке а. 2. Функция определена в точке а и её окрестности но не существует limx→a f(x). 3. Функция определена в точке а и её окрестности и существует limx→a f(x) но он ≠f(a). Точка а – точка разрыва 1-ого рода функции y=f(x) если в этой точке существуют конечные односторонние пределы функции т.е. limx→a-0 f(x)=А1, limx→a+0 f(x)=А2 при этом:а) если А1=А2 то точка а – точка устранимого разрыва. б)если А1≠А2 то точка а – точка конечного разрыва значения (А1-А2)- скачок функции в точке разрыва x=a. Точка а – точка разрыва 2-ого рода y=f(x) если по крайней мере 1 из односторонних пределов не существует.

9. Физический смысл производной. Правило дифференцирования.Пусть некоторая материальная точка m движется прямолинейно и и задан з-н его движ. s=s(t) т.е известен путь которая прошла точка m от некоторой начальной точки отсчёта в момент вр.(t). Тогда в момент вр.(to)точка пройдёт расстояние s(to),а в момент вр. to+^t- расстояние s((to)+(^t)) за промежуток вр. ^t точка пройдёт расстояние ^s=s(to+^t)-s(to). Отношение ^s/^t можно рассм.как среднюю скорость движ. на промежутке вр.to;(to+^t). И чем меньше промежуток вр. ^t,тем точнее соотв. средняя скорость будет х-тьдвиж. точки в момент вр. to. Поэтому предел средней скорости движ. при ^t=0 наз. скоростью движ. точки m в момент вр.(to). И обознач. v(to)

V(to)=lims(to+^t)-s(t0)/^t=s’(to) Таким образом, скорость движ. в момент вр.to есть производная пути по вр.

Правило дифференцирования

Если функция u=u(x) и v=v(x) имеет производные в точке x,то сумма, разность, произведение и частное этих функции также имеет произв. В данной точке. (u+-v)’=u’+-v’;(uv’)=u’v+v’u;(u/v)’=u’v-v’u/v2

Утверждение. Если ф-цияy=f(x) строго монотонна и непрерывна в некоторой окрестности точки xo, имеем производную в точке xo и f’(xo)не равно нулю, то обратная ф-цияx=f-1(y) имеет в соотв.точкеyo, yo=f(xo),причём (f-1)(yo)=1/f’(xo)

Утверждение. Если ф-цияu=m(x) имеет в точке xo произвольную, а ф-цияy=f(u) имеет соотв.точки (uo=m(xo)),производную f’(uo),то сложная ф-цияy=f(m(x)) имеет произв.в точке xo и справедлива формула:

y’(xo)=f’(uo)m’(xo)

10.Производная сложной функции. Логарифмическая производная. Таблица производных. Если функция u=Ф(x) имеет в т.X 0 производную y=f(u), а функция имеет в соотв. Точке

u 0 =Ф(X 0)производную f’(ф0), то сложная функция y=f(Ф(x)) имеет производную в точке X 0 и справедлива формула: y’(X 0)=f’(u 0 )*ф’(X 0)

Логарифмическая производная:

Пусть f(x)>0 , тогда рассмотрим функцию y= ln(f(x)) . диф-ем эту функцию, как сложную где y= lnu, u=f(x) получим

(ln(f(x)))’=(lnu)’*f’(x)*f’(x)/f(x)

Производная от лог некоторой функции наз лог производной этой ф-ции, а послед применение операции логарифмирования , а затем диф-нияназ лог диференциалом

Табл: 1)(x^α )᾽=αx^(α-1); 2)(1/x)᾽=1/x^2 ; 3) (√x)=1/(2√x); 4) (a^x )᾽=a^xln⁡a; 5) (log_a⁡x )᾽=1/(x ln⁡a ) ; 6)〖(ln〗⁡x)᾽=1/x; 7)(sin⁡x )=cos⁡x;8) (cos⁡x)᾽= -sin⁡x; 9)(tgx)᾽=1/(〖cos〗^2 x);10)(ctgx)᾽=(-1)/(〖sin〗^2 x); 11)(arcsinx)᾽=1/√(1-x^2 ); 12)(arccosx)᾽= - 1/√(1-x^2 ) .