Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

«ЧЕЛЯБИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

ИНСТИТУТ НЕПРЕРЫВНОГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

Отделение бизнеса и информатики

Контрольная работа

по дисциплине:

Эконометрика

(вариант №4)

Студент: Юнусова З. В.

Группа: 32 ЭС-301

Научный руководитель:

Постников Е. А.

Челябинск 2011

Исходные данные

Имеются данные о сменной добычи угля Y (тонн) на одного рабочего и мощности пласта Х (в метрах).

№	X	Y
1	22,7	5,4
2	25,8	7,2
3	20,8	7,6
4	15,2	4,4
5	25,4	7,5
6	19,4	6,7
7	18,2	6,2
8	21,0	6,4
9	16,4	5,5
10	23,5	6,9
11	18,8	5,4
12	17,5	6,3

где N – номер варианта студента

Задание

Исследовать зависимость сменной добычи угля на одного рабочего от мощности пласта путем построения уравнения парной линейной регрессии

.

Для исходных данных, приведенных в задаче, требуется

1. Построить поле корреляции и сформулировать гипотезу о форме связи.

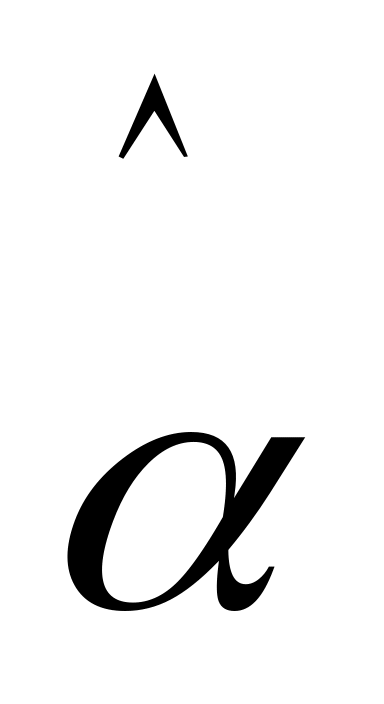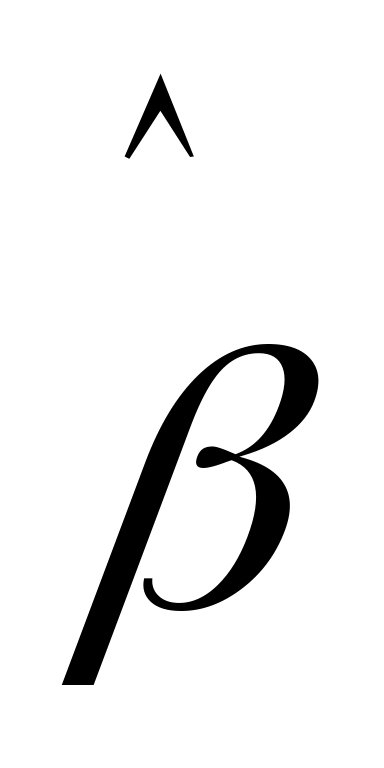2. Найти оценки и параметров модели парной линейной регрессии и 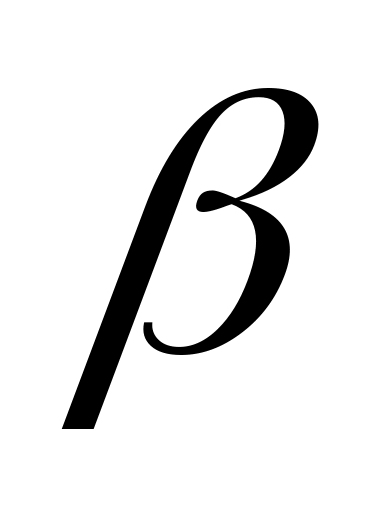. Записать полученное уравнение регрессии.

3. Проверить значимость оценок коэффициентов и с надежностью 0,95 с помощью t-статистики Стьюдента и сделать выводы о значимости этих оценок.

4. Определить интервальные оценки коэффициентов и с надежностью 0,95.

5. Проверить при уровне значимости 0,05 значимость уравнения регрессии с помощью F-статистики Фишера и сделать выводы о значимости уравнения регрессии.

6. Определить коэффициент детерминации R² и коэффициент корреляции r_xy. Сделать выводы о качестве уравнения регрессии.

7. Рассчитать среднюю ошибку аппроксимации и сделайте выводы о качестве уравнения регрессии.

8. Рассчитать прогнозное значение результата 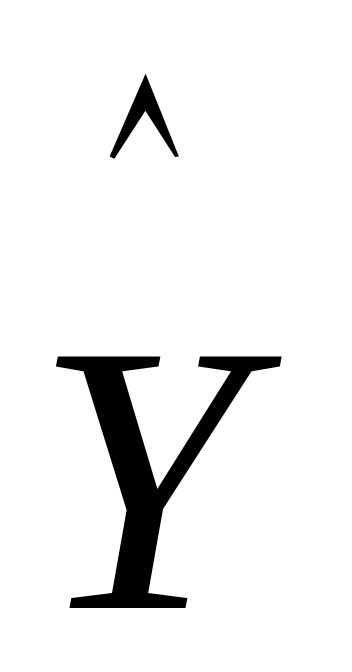, если значение фактора X будет больше на 15% его среднего уровня .

9. Дать экономическую интерпретацию коэффициентов парной регрессии.

Решение:

1. Построить поле корреляции и сформулировать гипотезу о форме связи.

Поле корреляции изображено на рис.1. Оно строится следующим образом: по горизонтальной оси откладывается фактор х, а по вертикальной фактор у.

8

7

6

5

4

3

2

1

0

0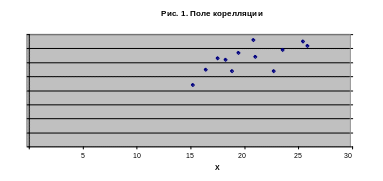

Выдвинем гипотезу о линейной форме связи.

2. Найти оценки и параметров модели парной линейной регрессии и . Записать полученное уравнение регрессии.

Линейная регрессия сводится к нахождению уравнения вида:

Построение линейной регрессии сводится к оценке ее параметров a и b. Классический подход к оцениванию параметров линейной регрессии основа на методе наименьших квадратов, который позволяет получить такие оценки параметров a и b, при которых сумма квадратов отклонений фактических значений результативного признака y от расчетных (теоретических) минимальна:

Строим систему нормальных уравнений для оценки параметров a и b:

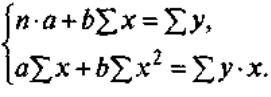
Решая данную систему найдем искомые оценки параметров a и b. Можно воспользоваться следующими формулами для a и b.

Параметр b называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу. Знак при коэффициенте регрессии b показывает направление связи: при – связь прямая, а при – связь обратная.

Составим таблицу для расчетов необходимых значений (таблица 1)

σ _x²=x² – x² = 426,606 - 20,392² = 10,786

σ _y²=y² – y² = 40,448 – 6,292² = 0,862

= 130,428 – 6,292 * 20,392 = 0,198

10,772

= 6,292 – 0,198 * 20,392 = 2,263

Уравнение линейной регрессии будет иметь вид:

= 2,263 + 0,198 * x

3. Проверить значимость оценок коэффициентов и с надежностью 0,95 с помощью t-статистики Стьюдента и сделать выводы о значимости этих оценок.

Процедура оценки значимости коэффициентов осуществляется следующим образом:

Рассчитывается значение t-статистики для коэффициента регрессии по формуле или .

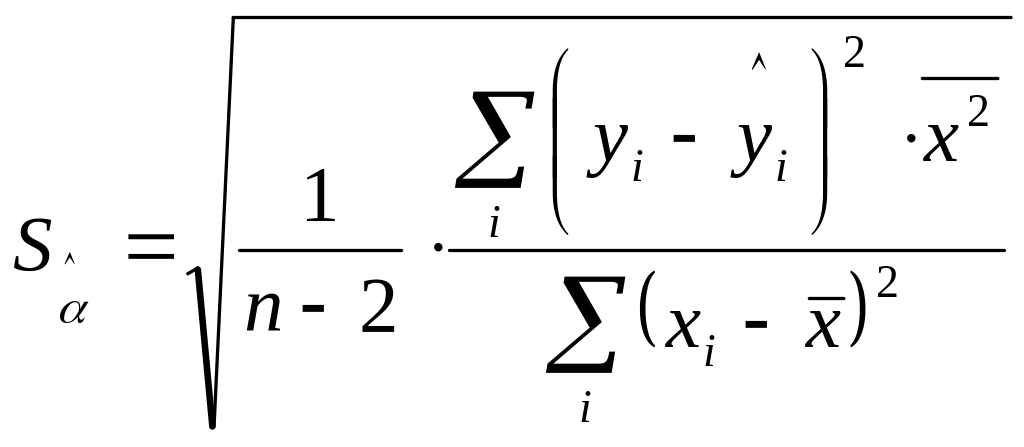
= ^{0,1 * 5,298*426,606} = 1,321

^129,429

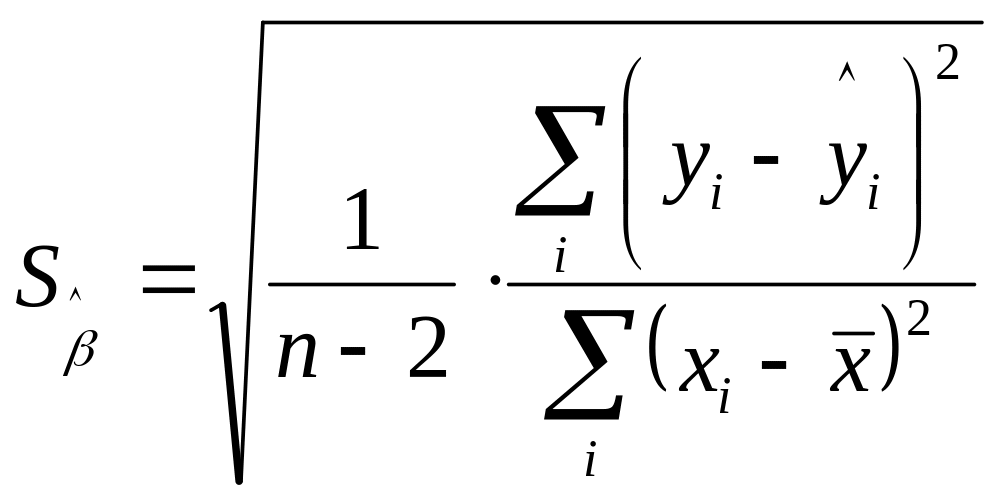
= ^{0,1 * 5,298} = 0,064

^129,429

= 2,263 / 1,321 = 1,7127

= 0,198 / 0,064 = 3,0878

1. Уровень доверия q = 0,95

2. Уровень значимости  = 1 – q = 1 – 0,95 = 0,05

3. Число степеней свободы n – 2 = 12 – 2 = 10

4. t_кр = 2,2281

5. Сравнение расчетных и табличных величин критерия Стьюдента показывает, что

t < t_кр ;

t > t_кр

Это значит, что коэффициент статистически незначим, а коэффициент статистически значим.

4. Определить интервальные оценки коэффициентов и с надежностью 0,95.

1. Уровень доверия q = 0,95.

2. Уровень значимости  = 1 – q = 1 – 0,95 – 0,05.

3. Число степеней свободы n – 2 = 12 – 2 = 10.

4. По таблицам распределения Стьюдента t_кр = 2,2281

5. Доверительные интервалы для параметров .

α: , α: ( -0,68 ; 5,206)

β: . β: (0,055 ; 0,34)

Точность коэффициента β высокая, а коэффициента α – низкая.