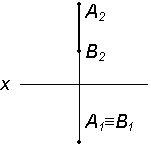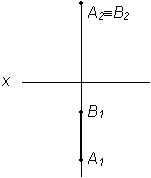6. Взаимное положение прямых линий.

Прямые частного положения – это прямые, которые либо параллельны (табл. 3.1), либо перпендикулярны одной из плоскостей проекций (табл. 3.2).

Прямые уровня

Всякую линию, параллельную плоскости проекций, называют линией уровня. В начертательной геометрии различают три основные линии уровня: горизонталь, фронталь и профильную линии (табл. 3.1).

Таблица 3.1

Прямые уровня

Определение	Наглядное изображение	Комплексный чертеж
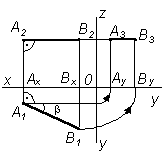
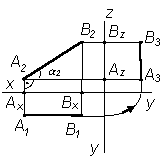
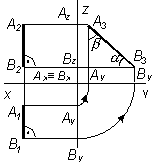
Горизонталью называют всякую линию, параллельную горизонтальной плоскости p1: A2B2   || Оx; A3B3i || y. A1B1 – натуральная величина отрезка, b – угол наклона к 2

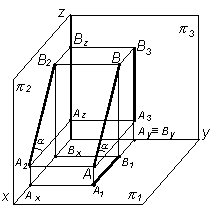
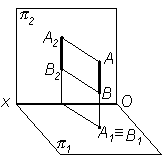
Фронталью называют линию, параллельную фронтальной плоскости 2: A1B1i  || Оx; A2B2 – натуральная величина; А3B3 i || z; – угол наклона к 1
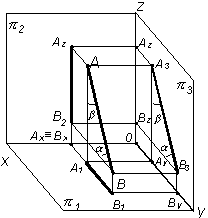
Профильной линией называют линию, параллельную профильной плоскости  3; A2B2i || z; A1B1i|| y; A3B3 – натуральная величина отрезка, – угол наклона к 1; – угол наклона к  2

Проецирующие прямые

Проецирующими прямыми называют прямые, расположенные перпендикулярно к плоскостям проекций ₁, ₂, ₃. Различают три основные проецирующие прямые: горизонтальную, фронтальную и профильную.

Если прямая перпендикулярна какой-либо из плоскостей проекций, то на эту плоскость она проецируется в виде точки. Две другие ее проекции параллельны осям и равны натуральной величине отрезка (табл. 3.2).

Таблица 3.2

Проецирующие прямые

Определение	Наглядное изображение	Комплексный чертеж
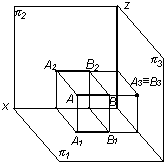
Горизонтально проецирующей прямой называют прямую, перпендикулярную к плоскости 1; A2B2 – натуральная величина AB, в плоскости 1 отрезок АВ проецируется в точку А1 В1

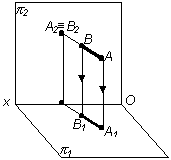
Фронтально проецирующей прямой называют прямую, перпендикулярную к плоскости 2; AB || 1 и AB 2, А1В1 – натуральная величина АВ, в плоскости 2 отрезок проецируется в точку А2 В2
Профильно проецирующей прямой называют прямую, перпендикулярную к плоскости 3; AB || 1 и AB || 2, А1В1 и А2В2 – натуральные величины отрезка АВ, А3В3 проецируется на 3 в точку

При сравнительном анализе изображений прямых частного положения на комплексном чертеже (табл. 3.1 и 3.2) следует:

1. Прямая уровня проецируется в натуральную величину на ту плоскость, которой она параллельна. Две остальные ее проекции обязательно параллельны осям проекций.

2. Проекция прямой уровня, к той плоскости, которой она параллельна, составляет с осями проекций углы, равные углам наклона линии уровня с плоскостями проекций.

3. Если прямая перпендикулярна плоскости проекций, то ее проекцией на эту плоскость является точка, а вторая проекция располагается перпендикулярно осям проекций.