Преобразования Фурье производной и производная преобразования Фурье.

Если непрерывная и абсолютно интегрируемая на функция f(x) является кусочно гладкой на любом отрезке , а функция абсолютно интегрируема на , то

.

Доказательство. Для функции f(x) справедлива фломула Ньютона-Лейбница

.

Так как производная абсолютно интегрируемая функция, то существует

.

Покажем, что A = 0. Если, например,A > 0, то существует такое число , что при x > a выполнено неравенство , откуда по признаку сравнения следует, что интеграл является расходящимся, что противоречит условию теоремы. Итак, .

Аналогично, доказывается, что .

Применяя интегрирование по частям, получаем равенство

.

Так как | e ^{− ixy} | = 1, то внеинтегральный член в правой части этого равенства обращается в нуль и, следовательно, справедливо равенство (6).

Если функция f(x) непрерывна на , а функции f(x) и xf(x) абсолютно интегрируемы на , то функция имеет на непрерывную произвудную, причем

.

Доказательство. Дифференцируя интеграл (3) по параметру y, получаем равенство

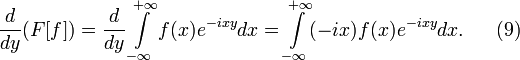
Обоснование законности дифференцирования под знаком интеграла сводится к проверке условий теоремы 6, 72. Интеграл сходится равномерно по пораметру y на по признаку Вейерштрасса, так как , а интеграл сходится.

Билет №20 Углы между прямыми и плоскостями.

Чтобы найти угол между двумя прямыми, следует найти их напрвляющие векторы и вычислить косинус угла между ними, используя скалярное произведение.

Для нахождения угла между прямой и плоскостью определяют угол θ между направляющим вектором прямой и нормальным вектором плоскости. Если векторы выбрать так, чтобы , и взять , то искомый угол дополняет θ до π / 2.

Угол между плоскостями находят как угол между их нормальными векторами.

Для двух прямых на плоскости

y = k₁x + b₁

y = k₂x + b₂

Получаем для угла между прямыми

если, знаменатель зануляется, то получаем, что прямые взаимно перпендикулярны.

Формула расстояния от точки до прямой и плоскости, между прямыми в пространстве.

Расстояние от точки до плоскости.

Пусть дана плоскость с уравнением и точка M с радиус-вектором R. Рассмотрим вектор , соединяющий начальную точку плоскости с M. Расстояние от точки до плоскости равно модулю его скалярной проекции на вектор , т.е.

.

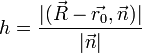Если в декартовой прямоугольной системе кооррдинат точка M имеет координаты (X,Y,Z), то равенство перепишеться в виде

Расстояние от точки до прямой.

Если прямая задана уравнением , то мы можем найти расстояние h от точки M с радиус вектором , до этой прямой, разделив площадь параллелограмма, построенного на векторах и , на длину его основания. Результат можно записать в виде

Рассмотрим прямую на плоскости, тогда получаем

Расстояние между скрещивающимися прямыми.

Пусть прямые p и q не параллельны. Известно, что в этом случае существуют такие параллельные плоскости P и Q, что прямая p лежит в P, а прямая q в Q. Расстояние h между P и Q называется расстоянием между прямыми p и q. Если p и q пересекаются, то P и Q совпадают и h = 0.

Для того чтобы найти расстояние h, проще всего разделить объем параллелепипеда, построенного на векторах , и , на площадь его основания. Мы получим