Интегральная теорема Коши.
Теорема Коши для случая непррывной производной.
Теорема 1. Пусть функция f(z) дифференцируема в односвязной области D и её производная непрерывна в D. Тогда интеграл от f(z) по любой замкнутой кривой γ, лежащей в области D, равен нулю:
.
Доказательство. Если f(z) = u(x,y) + iv(x,y), то по формуле
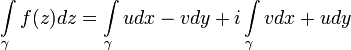
имеем
,
где
.
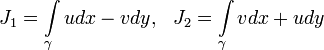Так как функция f(z) имеет непрерывную производную в области D, то частные производные первого порядка функции u,v непрерывны в области D и выполняется условия Коши-Римана
В силу применимости формулы Грина следует, что J1 = J2 = 0. Таким образом
Билет №34 Интегральная формула Коши.
Пусть функция f(z) дифференцируема в односвзяной области D и пусть простая замкнутая кривая γ лежит в D и ориентирована положительно. Тогда для любой точки z, лежащей внутри γ, справедлива формула
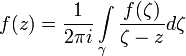
это формула называется интегральной формулой Коши.
Доказательство. Функция f(ζ) / (ζ − z) дифференцируема в области D с выколотой точкой z. Выберем ρ так, чтобы круг | ζ − z | < ρ вместе с его границей Cρ: | ζ − z | = ρ лежал внутри γ. Тогда используя следствие из интегральной теоремы Коши, получаем
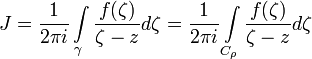
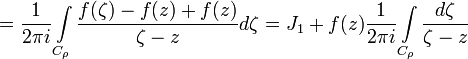
где
.
Так
как
,
то
и пожтому для доказательства достаточно установить, что J1 = 0.
В
силу непррывности функции f(ζ) в
точке z для любого
найдется
такое
,
что неравенство
выполняется
при | ζ − z | < δ. Следовательно
,
если
.
Учитывая, что J1 не зависит от
ρ, получаем J1 = 0, т.е. J =
f(z). Формула доказана.
Разложение функции, регулярной в окрестности точки, в ряд Тейлора.
Если
функция f регулярна в круге Br(a),
где
,
то она представима в этом круге Br(a)
в виде суммы сходящегося ряда Тейлора,
т.е.
,
где
.
Доказательство.
Фиксируем
произвольную точку
.
Тогда существует число r1 >
0 такое, что | z − a | < r1
< r. Пусть
-
ориентированная движением против хода
часовой стрелки. Запишем интегральную
формулу Коши:
.
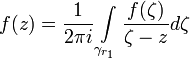Преобразуем
функцию
,
где
,
к виду
Получаем разложение в сходящийся ряд
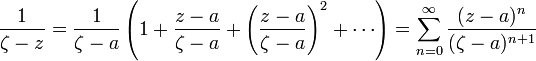
В
итоге подинтегральная функция представима
сходящимся на
рядом
.
Ряд сходится равномерно на окружности . Поэтому ряд можно почленно интегрировать по окружности . В результате получаем равенство
.
т.е. степенной ряд вида с коэффициентами
Эти коэффициенты cn не зависят от выбора точки z или окружности , так как воспользовавшись формулой для производной получаем для cn необходимую формулу.
Билет №35 Разложение функции, регулярной в кольце в ряд Лорана.
Всякая
функция ω = f(z), регулярная в
кольце ρ < | z − a | < R, где
,
представима в этом кольце суммой
сходящегося ряда Лорана
,
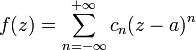коэффициенты которого определяются по формулам
,
где
,
причем ориентация окружности | ζ − a | = r положительная.
Доказательство.
Покажем
что каждый коэффициент cn
в формулу не зависит от выбора
.
Функция
регулярна
в кольце ρ < | ζ − a | < R. Для
любых чисел
определим
окружности
.
По обобщенной теореме Коши получаем
равенство
что
и требовалось для доказательства
независимости интеграла от выбора
при
каждом
.
Зафиксируем
произаольную точку z0 в кольце
ρ < | z − a | < R. Выберем числа
r1,r2 такие, что ρ <
r1 < | z0 − a | <
r2 < R, и окружности
ориентированные
положительно. Тогда контур
,
является границей кольца r1 <
| z − a | < r2, в котором
по интегральной формуле Коши получаем
.
Рассмотрим интеграл I2. Повторяя рассуждения для вывода формулы Тейлора получаем
где
Рассмотрим
интеграл I1. Представим
в
виде ряда
По признаку Вейерштрасса ряд сходится равномерно , его можно почленно интегрировать, получаем
Заменяя в формуле номера (n + 1) на ( − m) получаем равенство
,
где
Так как точка z0 была выбрана в данном кольце произвольно, то складывая ряды получаем ряд Лорана.