Когда не существует базис из собственных векторов матрицы коэффициентов системы.

Рассмотрим нормальную линейную однородную ситему

Лемма 3. Каждая из вектор-функций является решением системы (1). где .

Теорема. Пусть жорданов базис в состоит из S жордановых цепочек длин k_j(k₁ + ... + k_S = n) для собственных значений λ_j преобразования A, j = 1,...,S.

Тогда:

а) вектор - функция фида

б) если x(t) - какое-либо решение системы (1), то найдется такой набор при котором x(t) задается в форме (2).

Доказательство.

a) немедленно следует из принципа суперпозиции и Леммы 3.

б) Пусть x(t) - какое-либо решение системы (1). Покажем, что оно имеет вид (5). При каждом решение x(t) можно раздожить по жордановому базису . Пусть

Подставим x(t) в (1) и воспользуемся определением жордановой цепочки. Имеем из единственности разложения

находим S систем вида:

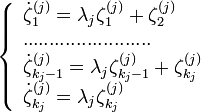
решая эти системы приходи к утверждению теоремы.

Билет №28 Линейные обыкновенные дифференциальные уравнения с переменными коэффициентами.

Рассмотрим линейную неоднородную систему

где - заданная непрерывная на [α,β] квадратная матрица порядка n, f(x) - заданная непрерывная на [α,β] вектор-функция с n компонентами.

Непосредственно проверяется следующее предложение, называемое принципом суперпозиции для системы (1).

Лемма. Если , y₁(x) - решение системы (1) при условии и y₂(x) - решение системы (1) при усоловии , то y(x) = y₁(x) + y₂(x) - решение системы (1).

Если известно какое-либо частное решение (1), то интегрирование линейной неоднородной системы (1) сводится к интегрированию соответствующей (1) линейной однородной системы

Теорема 1. Пусть y₀(x) - некоторое частное решение (1), и Φ(x) - фундомениальная матрица (2). Тогда все решение системы (1) задаются формулой

y(x) = Φ(x)c + y₀(x),

где c - произвольный числовой n-мерный вектор.

Доказательство. В системе (1) сделаем замену

y(x) = z(x) + y₀(x).

Тогда получаем, что z(x) удовлетворяет системе (2). Общее решение системы (2), как установлено в 2, имеет вид

где c - произвольный числовой n-мерный вектор. Из замены следует утверждение теоремы.

Теорема 2. Если Φ(x) - фундаментальная матрица линейной однородной системы (2), то общее решение линейной неоднородной системы (1) при всех задается формулой

где и d - произвольный числовой n - мерный вектор.

Доказательство. Согласно Лагранжу ищем решение (1) в таком же виде (3), что и решение однородной системы (2), но считаем c не постоянным, а непрерывно дифференцируемым вектором c(x), :

.

При таком переходе от y(x) к c(x) потери решений (1) не происходит, так как . Ниже будет видно, что такая замена неоднозначна. Функцию c(x) находим подстановкой y(x) в систему (1). Используя формулу производной произведения матрицы и вектор-функции, получаем, что

Φ'(x)c(x) + Φ(x)c'(x) = A(x)Φ(x)c(x) + f(x).

Поскольку

Φ'(x) = A(x)Φ(x),

то Φ(x)c'(x) = f(x). Так как матрица Φ(x) невырожденная на [α,β], то отсюда

.

Это уравнение можно интегрировать, поскольку - непрерывная вектор-функция на [α,β]. Проинтегрировав последнее уравнение, получаем утверждение теоремы.