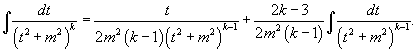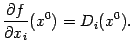28.первообразная и неопределеннный интеграл.Пусть функция f(x), заданная в некотором промежутке^* [a, b], во всех его точках является производной функции F(x) , также заданной в [a, b]. Тогда эта последняя функция F(x) называется первообразной функцией для функции f(x) (в промежутке [a, b])  Имеет местоТеорема 1. У всякой непрерывной на промежутке [a, b] функции имеется первообразная.   Доказательство этой теоремы будет дано далее. Нетрудно видеть, что, если функция F(x) есть первообразная для f(x), то функция F(x) + C при любом постоянном C также является первообразной для f(x). В то же время никаких других первообразных, кроме функций вида F(x) + C, у f(x) уже быть не может. Действительно, еслиF₁(x) есть какая-то первообразная для f(x), то производная разности F₁(x) - F(x) будет всюду на [a, b] равняться нулю, а тогда сама разность есть величина постоянная, т. е. F₁(x) - F(x) = C     и     F₁(x) = F(x) + C..  Если F(x) есть первообразная функция для f(x), то функция двух аргументов x и C, равная F(x) + C, называется неопределенным интеграломфункции f(x) и обозначается символом.. Теорема 2. Производная неопределенного интеграла равна подинтегральной функции, т. е.

  1.  .      

     2.  .

     3.  .

     4.  .

     5.  .

     6.  .

     7.  .

     8.  .

     9.  .

     10.  .

     11.  .

     12.  .

    Основные свойства

     1.     

     2.     

     3. Если   то

     4. 

Свойства неопределенного интеграла:

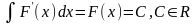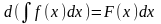1. 2. 3.

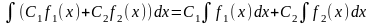
Вычисление интегралов с помощью непосредственного использования таблицы простейших интегралов и основных свойств неопределенных интегралов называется непосредственным интегрированием.  Пусть каждая из функций f(x) и g(x) д-ма множестве Х и, кроме того, на этом множестве существует первообразн. для ф-и g(x)   f '(x). Тогда на мн-ве Х существует первооб. для ф-и f(x)g '(x), причем верна ф-ла: 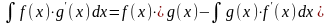. Замечание: Определение дифференциала и свойство инвариантности его формы позволяет записать формулу в виде: . 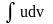Формула сводит вопрос о вычислении интеграла к вычислению интеграла 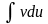. Применяется для интегралов вида: .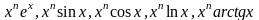

Например: 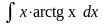. u= arctg x dv= xdx, отсюда: 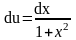, v=x²/2.

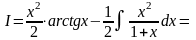
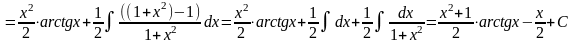
П. И н.И.: Формула замены переменных под знаком интеграла.

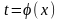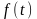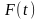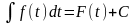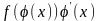Пусть функция определена и дифференцируема на некотором множестве {х} и пусть {t } — множество значений этой функции. Пусть далее для функции существует на множестве {t} первообразная функция , т.е. . Тогда всюду на мн-ве {х} для функции существует перв-я функция, равная 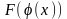, т.е.

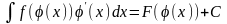
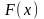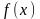Док-во путем интегрирования формулы для сложной функции.  — первообразная , тогда — первообразная функции , что и требовалось доказать.

Например: 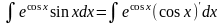. Заменяем cos x на t.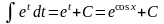

29. Для интегрирования рациональной функции  , где P(x) и Q(x) - полиномы, используется следующая последовательность шагов:1)Если дробь неправильная (т.е. степень P(x) больше степени Q(x)), преобразовать ее в правильную, выделив целое выражение; 2)Разложить знаменатель Q(x) на произведение одночленов и/или несократимых квадратичных выражений;3)Разложить рациональную дробь на простейшие дроби, используя метод неопределенных коэффициентов;4)Вычислить интегралы от простейших дробей.

1. 

2. 

У дробей с квадратичным знаменателем сначала необходимо выделить полный квадрат:

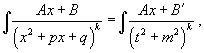
где   Затем применяются следующие формулы:

3. 

3. 

3. 

Интеграл   может быть вычислен за k шагов с помощью формулы редукции

6. 

8. Интегрирование тригонометрических функций

9. 1°. Интегралы вида

10. 

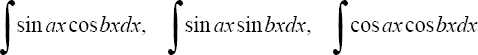
11. находятся с помощью тригонометрических формул

12. 

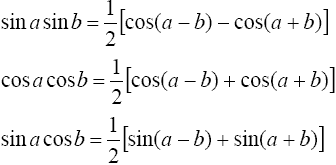
13. 2°. Интегралы вида

14. 

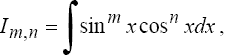
15. где m и n - четные числа находятся с помощью формул понижения степени

16. 

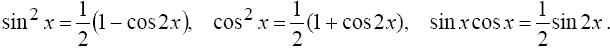
17. Если хотя бы одно из чисел m или n - нечетное, то полагают (пусть m = 2k + 1)

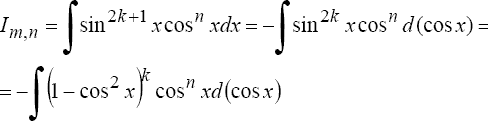
30 ВопросИнтегрирование биномиальных дифференциалов

рационализуется лишь в трех случаях

     1)   подстановка   где k - общий знаменатель m и n;

     2)   подстановка   где k - знаменатель p;

     3)   подстановка   где k - знаменатель p.

.

 Интегрирование дробно–линейных иррациональностей

R  ж з и x, p√  ax + b cx + d ,  q√ ax + b cx + d ,  … ц ч ш

(1)

где R — рациональная функция и p , q,  … — натуральные числа.

При вычислении интегралов от функций вида (1) с помощью подстановки

x   =    tnd − b a − ctn  ,         tn   =    ax + b cx + d  ,

где n — общий знаменатель дробей 1/p, 1/q,  … , приходим к интегралам от рациональных функций t .

 Интегрирование квадратичных иррациональностей

R(x, √ a2 ± x2 )  и  R(x, √ x2 − a2 )

где R — рациональная функция.

а) Для интегрирования выражений R(x, √

a2 − x2

) используются подстановки

x = a · sin t     или     x = a · cos t .

б) Для интегрирования выражений R(x, √

a2 + x2

) dx используются подстановки

x = a · tg t     или     x = a · sh t .

в) Для интегрирования выражений R(x, √

x2 − a2

) dx используются подстановки

x = 

a

cos t

     или     x = a · ch t .

Во всех случаях, применив формулу замены переменной в неопределенном интеграле, получаем интегралы вида

∫ Rs(sin t, cos t) dt ,

31:

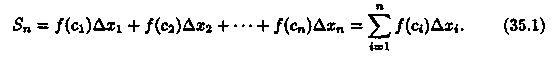
Сумма вида (35.1) называется интегральной суммой функции у = ƒ(х) на отрезке [а; b]. Обозначим черезλ длину наибольшего частичного отрезка: λ = max ∆x_i(i = 1,2,..., n).

Основные свойства определенного интеграла I). Величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е.  , где х, t – любые буквы.

2). Определенный интеграл с одинаковыми пределами интегрирования равен нулю.

3)I. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный.

4). Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам.

5). Постоянный множитель можно выносить за знак определенного интеграла.

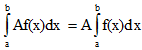
6). Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций.

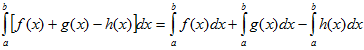
Формула Ньютона-Лейбница обычно записывают так: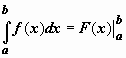 

32) 1. Вычисление площади плоской фигуры

 

1.1. Пусть функция   непрерывна и неотрицательна на отрезке [a, b]. Тогда площадь фигуры, ограниченной осью ОХ, отрезками прямых x = a, x = b и графиком функции  , может быть вычислена по формуле 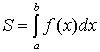  (см. 10.1 рис. 1).

1.2. Если   на отрезке [a, b],    непрерывные функции, то площадь фигуры, ограниченной прямыми х = а, x = b, графиками функций   вычисляется по формуле 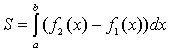  (рис. 10).

1.3. Если функция   на отрезке [a, b] принимает значения разных знаков, то площадь фигуры, заключенная между кривой   и осью  , равна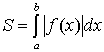 

33)несобственный интеграл…Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий:

• Предел a или b (или оба предела) являются бесконечными;

• Функция f(x) имеет одну или несколько точек разрыва внутри отрезка [a, b].

34 функции нескольких неременных .частные производные.

Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует.

частные производные – это почти то же самое, что и «обычные» производные функции одной переменной. 

Для частных производных справедливы все правила дифференцирования и таблица производных элементарных функций. Есть только пара небольших отличий, с которыми мы познакомимся прямо сейчас.

Пример 1

Найти частные производные первого и второго порядка функции 

Сначала найдем частные производные первого порядка. Их две.

Обозначения:  или   – частная производная по «икс»  или   – частная производная по «игрек»

Начнем с  . Когда мы находим частную производную по «икс», то переменная   считается константой (постоянным числом).

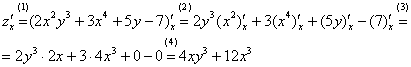
Связь частной производной с дефер.  Пусть функция   дифференцируема в точке   . Докажем, что тогда в точке   существуют частные производные по всем переменным   , причём если

то

(7.3)

        Доказательство.     Рассмотрим приращения вида   , где   . Тогда   и   при   . Поскольку   , приращение функции имеет вид

Разделив обе части на   и переходя к пределу при   , получаем:

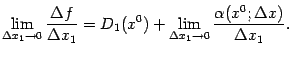
Второе слагаемое даёт 0, поскольку

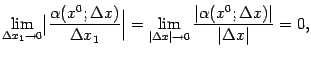
по предположению о дифференцируемости.

Левая часть же даёт частную производную по   , поскольку точка   при приращении указанного вида находится на прямой, проходящей через точку   параллельно оси   . Значит,

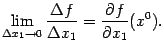
35) эксремум функций 2 переменных.Максимум и минимум функции называются экстремумами функции.

Теорема (необходимое условие экстремума функции двух переменных). Если функция   достигает экстремума при  , то каждая частная производная первого порядка от   или обращается в нуль при этих значениях аргументов, или не существует.

Достаточные условия

Теорема (достаточное условие экстремума функции двух переменных). Пусть в некоторой области, содержащей точку   функция   имеет непрерывные частные производные до третьего порядка включительно. Пусть, кроме того, точка   является критической точкой функции  , т.е. 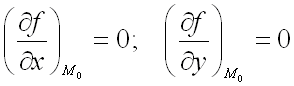, тогда при  : 1)   имеет максимум, если дискриминант   и  , где 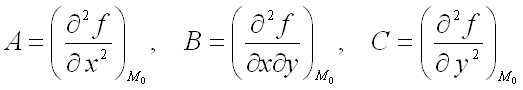 ; 2)   имеет минимум, если дискриминант   и  ; 3)   не имеет ни минимума, ни максимума, если дискриминант  ; 4) если   , то экстремум может быть, а может и не быть (требуется дополнительное исследование).