21. Если процесс нагрузки порта является пульсирующим процессом, то данный процесс называется пульсирующей нагрузкой и обозначается символами gi (произвольный независимый).

В многоканальной системе с потерями, с пульсирующей нагрузкой порта и экспоненциальным временем обслуживания GI/M/s(0) (см. рис.12) эпохи поступления вызова становятся пульсирующими точками и составляют внедренную (вложенную) Марковскую цепь.

Вероятность П_j того, что j вызовов существует как раз перед поступлением тестового вызова определяется как

(26)

где – вероятность перехода, при котором состояние (число вызовов, существующих в системе) изменяется скачком от i к j между двумя последовательно наступающими эпохами;

A(t) – будущая функция распределения промежутка времени между поступлениями;

 ^{– 1} – среднее время обслуживания.

В ероятность перехода p_ij интерпретируется следующим образом. Если i вызовов существует как раз перед наступлением эпохи предшествующего вызова, то сразу после поступления вызова число присутствующих вызовов становится (i+1). Таким образом, правая сторона выражения p_ij представляет вероятность того, что j из (i+1) вызовов продолжат существовать как раз перед наступлением эпохи поступления тестового вызова.

Генерирующая функция от вероятности П_j определяется из выражения (26) как

(27)

Вероятность блокировки (вероятность перегрузки по вызовам) определяется как

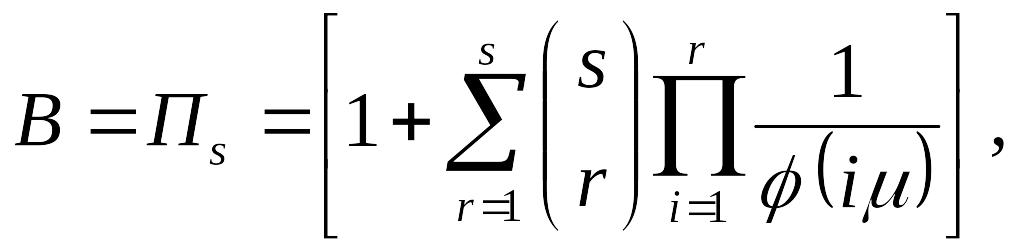(28)

где , а a*(θ) – LST от A(t).

Вероятность перегрузки по времени (вероятность того, что все сервера заняты) определяется как

(29)

где  – темп поступления;

a = / – предлагаемая нагрузка.

Многоканальная система с запаздыванием и бесконечным буфером с FIFO дисциплиной обслуживания очереди GI/M/s характеризуется следующими показателями качества:

(а) вероятность ожидания

(б) среднее число ожидающих вызовов (30)

(в) среднее время ожидания

где h =  ^–1 – среднее время обслуживания;

 = a*([1 – ]s) – обобщенное занятие, (0 <  < 1).

Распределение времени ожидания с FIFO порядком обслуживания очереди по аналогии с M/M/1 задается функцией дополнительного распределения:

M(t) = M(0) e ^{– (1 –  ) s t / h}. (31)

Граничная вероятность существования в системе GI/M/s точно s вызовов как раз перед поступлением вызова определяется как

(32)

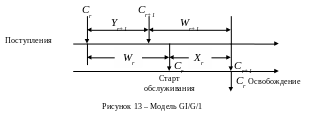
22. Точный анализ для однолинейного сервера GI/G/1 может быть задан с использованием спектрального решения. Для r-того вызова, поступающего в систему, обозначим время обслуживания – X_r , время ожидания – W_r , а промежуток времени между r-тым и (r + 1)-ым вызовами – Y_r+1 (см. рис.13). Отсюда определим время ожидания обслуживания (r + 1)-ым вызовом как

W_r+1 = (W_r + X_r – Y_r+1) ⁺ , (33)

где (z) ⁺ = max(0, z), которое равно z, если z  0; или 0, если z < 0.

Известно, что устойчивое состояние существует, если и только если коэффициент использования сервера  = h < 1 с темпом поступления  и средним временем обслуживания h. Устремив r   , получим W_r  W и (X_r – Y_r+1)  U. Тогда из выражения (33) будем иметь

W = (W + U) ⁺. (34)

Обозначив u(t) функцию плотности от U, а W(t) – функцию распределения времени ожидания, получим уравнение интеграла Линдлея:

(35)

Введем вспомогательную функцию W_(t), определенную так, что уравнение (35) справедливо для –  < t < 0 , и получим выражение:

(36)

Так как U есть разница между временем облуживания X и промежутка времени между вызовами Y, LST от U дается выражением

u*(θ) = a*(θ) b*( – θ), (37)

где a*(θ) и b*(θ) есть LSTs от X и Y, соответственно.

Обозначив преобразование Лапласа (LT) от W(t) символом W*(θ), и, произведя LT преобразования выражения (36), получим

W*(θ) [a*(θ) b*(θ) – 1] = W*_(θ). (38)

Предположим, что уравнение (38) имеет спектральные множители в виде

a*(θ) b*(θ) – 1 = (39)

которые удовлетворяет следующим условиям:

(а) спектральный множитель есть аналитический для Re(θ) > 0 c ненулевыми значениями и

(б) спектральный множитель есть аналитический для Re(θ) < D c ненулевыми значениями и

где D есть положительное действительное число.

Поставляя спектральные множители (39) в уравнение (38), получим

W*(θ) = W*_(θ) . (40)

Из условий (а) и (б) обе стороны уравнения (40) аналитически определены в области 0 < Re(θ) < D, они могут быть равны константе, скажем, К. Так как LST от W(t) определяется как *(θ) = θ W*(θ), то константа К определяется как

(41)

Используя предельное отношение *(θ)  1 при θ  0, мы получим вероятность того, что нет ожидания:

(42)

а LST распределения времени ожидания определится как

(43)

Произведя обратное преобразование *(θ), мы можем вычислить распределение времени ожидания, а дифференцирование *(θ) при начальных условиях дает моменты времени ожидания. Например, мы имеем среднее время ожидания

(44)

В однолинейной модели H₂/G/1 с гиперэкспоненциальным распределением промежутков времени между поступающими вызовами и с произвольным временем обслуживания LST сервисного времени (обслуживания) определяется как

(45)

где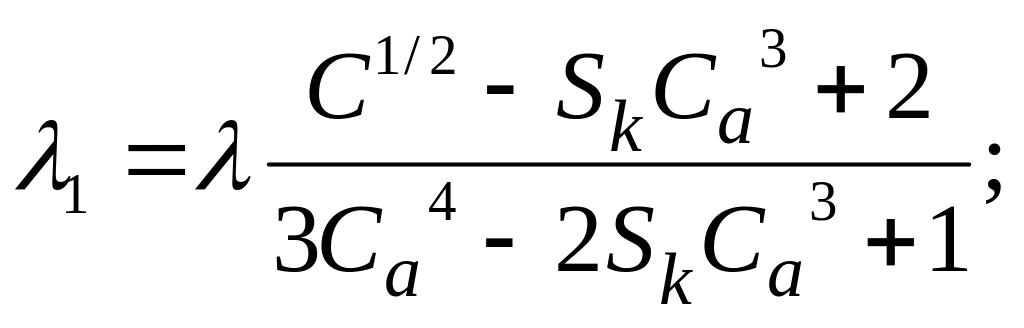

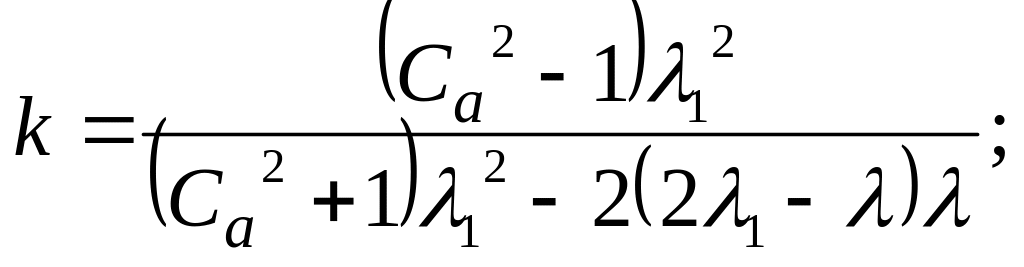
 – темп поступления;

С_а² – SCV промежутков времени между поступающими вызовами;

S_k – асимметрия (третий центральный момент или дисперсия^3/2) промежутков времени между поступающими вызовами.

В частном случае для симметричных условий асимметрия не востребуется и вычисления упрощаются:

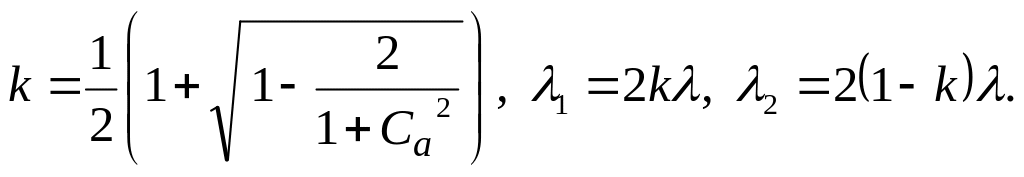при мы будем иметь: (46)

Спектральное решение для модели H₂/G/1 дает следующие результаты. Полагая, что

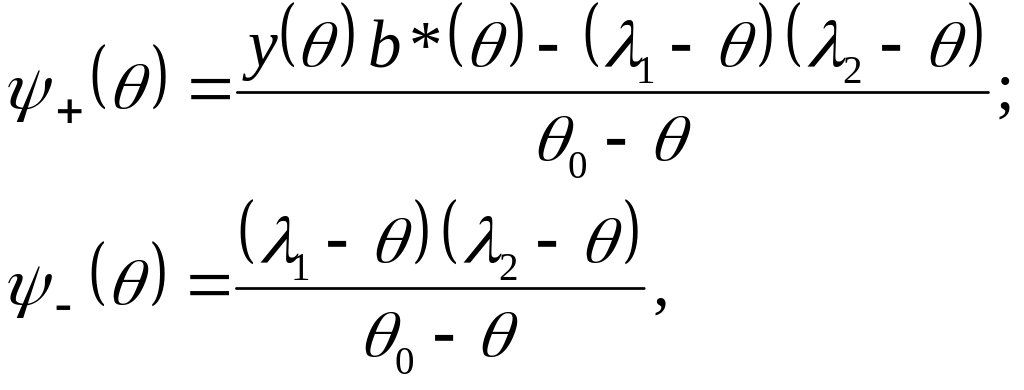(47)

мы можем удостовериться, что выражения (47) удовлетворяют условиям (39) с D = min(₁, ₂, Re(θ₀)). Здесь θ₀ есть корень функционального уравнения

y(θ) b*(θ) – (₁ – θ)(₂ – θ) = 0 , (48)

где y(θ) = k₁(₂ – θ) + (1 – k) ₂(₁ – θ) ,

b*(θ) – LST от Y.

Корень θ₀ можно вычислить итеративно с начальной величиной θ₀ = :

, (49)

где z(θ) ≡ ₁ + ₂ – [k₁ + (1 – k) ₂] b*(θ).

Из выражений (42)-(44) получаем следующие результаты:

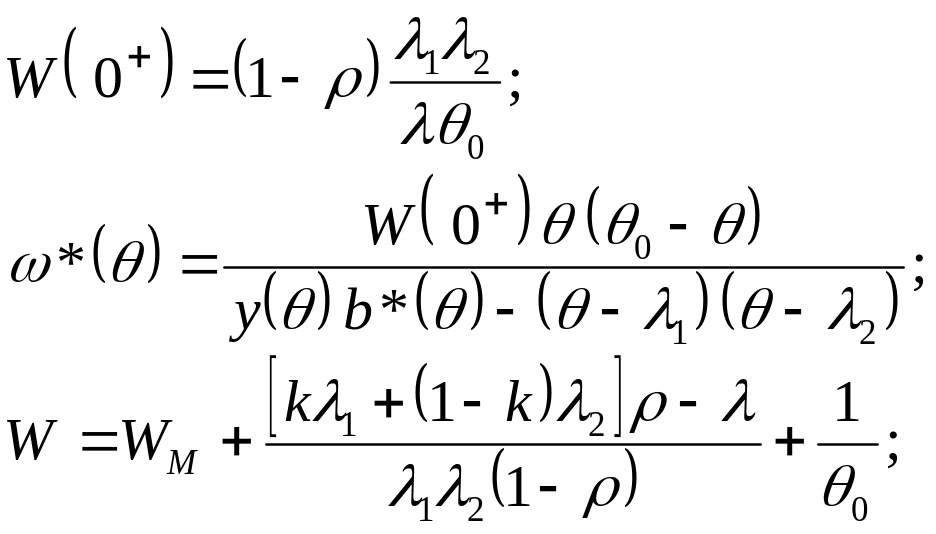(50)

где W_M – среднее время ожидания, эквивалентное и для системы M/G/1 (с тем же темпом поступления вызовов), и определяется из формулы Полячека-Хинчина (21) с SCV распределения сервисного времени.

Рассмотрим k-фазную Эрланговую нагрузку порта однолинейного сервера с произвольным временем обслуживания E_k/G/1. Известно, что LST k-фазного Эрлангового распределения промежутков времени между вызовами E_k определяется как

(51)

Применяя спектральное решение подобно ранее описанному способу, получим следующие результаты:

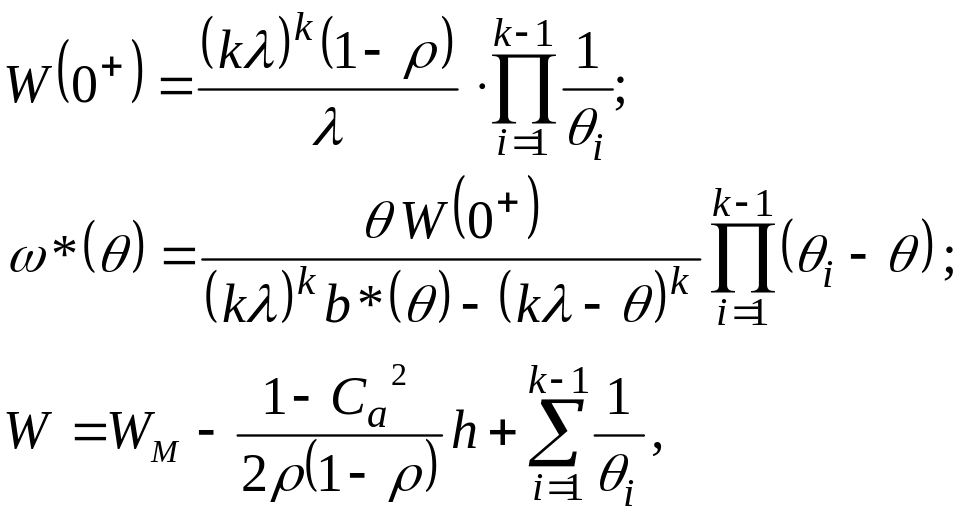(52)

где θ_i , i = 1, 2, … , k – 1, являются корнями уравнения функционала с Re(θ_i) > 0: (k)^kb*(θ) – (k – θ)^k = 0. (53)

Поставив в функционал (53) b*(θ) =  exp(j) c j = , вычислим эти корни итерационно

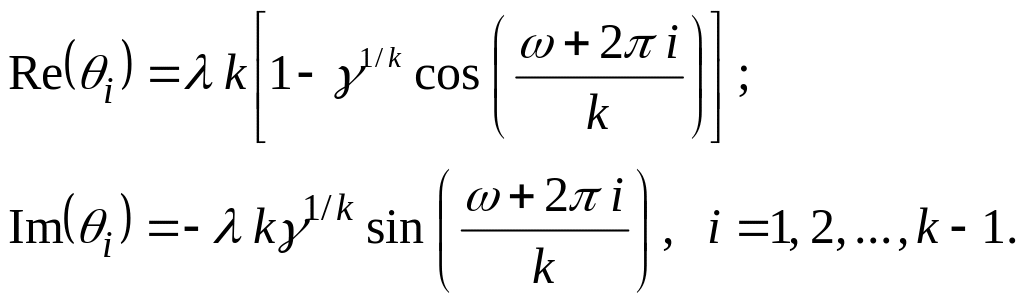(54)

Если k четное число, то мы имеем один действительный корень и (k/2 – 1) сопряженных пар; если k нечетное число, то мы имеем (k – 1) сопряженных пар. Отсюда ∏ θ_i и ∑1/ θ_i становятся действительными.

Можно заметить, что результаты (52)-(53) являются справедливыми только для целых k и асимметрия промежутков времени между поступающими вызовами определяется неявно. В расширенной версии для действительных чисел k имеют силу данные первых трех моментов.

25. Модели с мульти-классной нагрузкой порта применяются в сетях ISDN и LAN (поступление группы, очередь приоритета, многоразмерные, смешанные с потерями и с запаздыванием, модели с мультиочередями и т.д.).

В сетях с пакетной коммутацией сообщение разбивается на пакеты, которые могут быть аппроксимированы как модель с групповым поступлением. Модель с групповым поступлением предполагает, что пакеты данного сообщения прибывают на пункт назначения одновременно.

Размером группы в модели называется случайная переменная Х, которая определяется по числу вызовов, одновременно пребывающих в группе. Если группа находит все сервера занятыми на момент поступления, то все вызовы в группе теряются. Если число свободных серверов меньше чем размер группы, то прием вызовов группы осуществляют по какой-либо одной из двух стратегий: PBAS / WBAS. При изучении материала темы следует усвоить принятые обозначения и показатели качества модели, назначение составляющих элементов диаграммы состояний перехода. Необходимо обратить внимание на различия, связанные с видом распределения (экспоненциальное, геометрическое и т.д.) поступающих потоков неординарных вызовов.

При расчете времени ожидания в модели следует пользоваться аппроксимацией по формуле Крамера и Лангенбаха-Белза и овладеть навыками пользования SCV C_a и C_s.

26. Известно, что мультисервер систем с потерями и произвольным временем обслуживания M/G/s(0) эквивалентен Марковской модели M/M/s(0), и вероятность блокировки здесь задается формулой Эрланга В. Кроме того, вероятность блокировки для системы с ограниченным числом входов от n источников M(n)/G/s(0) задается потерями по формуле Энгсета. Данные свойства относятся к робастности сервисного времени.

Известно, что система M/G/1 имеет устойчивое состояние, если и только если предлагаемая транспортная нагрузка a =  = h < 1 erl, где h есть среднее время обслуживания, а  – коэффициент использования системы. Это может быть понято интуитивно, потому что сервер может обслужить 1 erl, как максимум.

Выберем некоторый вызов и пометим его как тестовый вызов (см. рис.10). Вероятность того, что сервер занят, когда тестовый вызов поступит, по свойству 3 нагрузки и PASTA равна а. Время до тех пор, пока не завершится обслуживание вызова, является остаточным сервисным временем. Отсюда, обозначив среднее остаточное время обслуживания символом , среднее число ожидающих вызовов – , а среднее время ожидания – , мы имеем при порядке обслуживания вызовов FIFO следующую зависимость:

= a + h. (18)

С правой стороны выражения (18) первое произведение соответствует среднему времени для вызова в обслуживании, если некоторый должен быть завершен, а второе произведение соответствует обслуживанию тех ожидающих вызовов, которые стоят в очереди впереди тестового вызова.

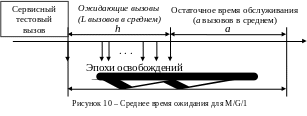
Используя формулу Литтла =  и решая зависимость (18), мы получим среднее время ожидания

(19)

Из выражения (16) мы получим среднее остаточное время

(20)

где C_s² = σ_s²/ h² – является SCV сервисного времени (обслуживания);

σ_s²– является дисперсией сервисного времени (обслуживания).

Подставляя среднее остаточное время (20) в среднее время ожидания (19), мы получим формулу Полячека-Хинчина:

(21)

В стохастическом процессе момент времени, в котором свойство марковости держится, называется пульсирующей точкой. Для системы M/G/1 эпоха депортации (освобождения), в которой вызов завершается и покидает систему, становится пульсирующей точкой.

Марковский процесс с дискретным пространством состояний называется Марковской цепью. В Марковской цепи все времена эпох, в которых состояние изменяется, становятся пульсирующими точками. С другой стороны, стохастический процесс называется внедренной (вложенной) Марковской цепью, если пульсирующие точки внедряются или вкладываются в особое время эпох, таких как депортация (освобождение) вызова в системах типа M/G/1.

Во внедренной Марковской цепи (см. рис.11) состояние вероятности П_j* как раз после освобождения (депортации вызова) равно состоянию вероятности П_j как раз перед поступлением вызова в устойчивом состоянии. Из PASTA следует, что если в системе M/G/1 существует j вызовов, то P_j = П_j = П_j* .

27.

29. Многоразмерный трафик определяется как вызовы с различными характеристиками, разделяющими общие ресурсы системы. Примеры включают смешанный трафик речевых сигналов и потоки данных с различными скоростями передачи (или шириной частотного диапазона), разделяющие общую группу каналов передачи. Необходимо ознакомиться с многоразмерной системой с потерями, в которой обслуживаются низкоскоростные (данные) и высокоскоростные (голос) вызовы. Пояснить причину возникновения эффекта дробления канала.

Система линейного резервирования используется для того, чтобы гарантировать степень обслуживания GOS льготного трафика за счет резервирования определенного числа линий под данный трафик. Изучите систему линейного резервирования и ознакомьтесь с численным методом анализа систем с запаздыванием, использующих схему линейного резервирования для двух классов трафика: приоритетного (высокоскоростные вызовы) и ординарного (низкоскоростные вызовы) трафика.

Ознакомьтесь с алгоритмом итеративного вычисления вероятностей устойчивого состояния при выполнении индивидуальных измерений показателей качества системы: среднего числа ожидающих вызовов, вероятности блокировки (вероятность переполнения буфера) и среднего времени ожидания для приоритетных и ординарных вызовов.

30. Системы с интегрированными вызовами, такими как голос, требующий обслуживания в реальном масштабе времени, а также отсроченные вызовы подобно данным, называются смешанными системами с потерями и с ожиданием. Такие системы интегрируются в сетях ISDN, где различные медиа разделяют сетевые ресурсы.

Показателями качества смешанной системы M₁+M₂/s(0,) являются взаимосвязанные потери и среднее время ожидание. Необходимо ознакомиться с данной взаимосвязью, научиться рассчитывать структурные параметры таких систем по заданным нагрузкам и решать обратную задачу, т.е. рассчитывать требуемую нагрузку по заданным потерям и среднему времени ожидания.

Системы GI+M/s(,0) и GI+M/s (0,) рассчитываются с использование так называемой пульсирующей аппроксимации GI. Известно, что объединение двух пульсирующих потоков, вообще говоря, не образует пульсирующего процесса. Вместе с тем выходной поток решаются аппроксимировать пульсирующей аппроксимацией. При этом получают аналитические решения (вероятность блокировки и среднее время ожидания).

31. Система, в которой число очередей обслуживаются согласно определенным дисциплинам, называется моделью с мультиочередями. В модели с мультиочередями циклического типа, которая применяется в системах голосования при передаче данных, где контроллер проверяет требования вызовов на каждой станции (очереди), обслуживает их при наличии и затем последовательно перемещается к следующей станции. Такая модель находит применение в эстафетном кольце Token Ring LAN, которое посылает маркер по узлам, связанным в топологию кольца, и только тому узлу позволяется приступить к передаче данных, который получил свободный маркер.

Модель с истощением: Сервер перемещается к следующей очереди после того, как обслужены все вызовы (требования) в очереди, включая и те, которые поступили в сервисный период.

Модель с запором: Сервер перемещается к следующей очереди после того, как обслужены вызовы, ожидающие в очереди и которые поступили перед началом обслуживания.

Модель с ограничением: Сервер перемещается к следующей очереди после того, как обслужено ограниченное (заданное) число ожидающих вызовов в очереди плюс те вызовы, которые поступили в сервисный период. Если первые k вызовов обслуживаются, то такая модель называется k-ограниченной.

В зависимости от дисциплины перемещения сервера среди очередей, модель с мультиочередями классифицируется как циклического типа, стохастического типа или приоритетного типа.

32. Анализ современных систем транспортировки информации невозможен без использования модели диффузии и метода матричного анализа. Такие системы, как пакетный мультиплексор в сетях ISDN и ATM, эстафетное кольцо LAN в стандарте Token Ring LAN и множественный доступ с опросом несущей и разрешением конфликтов в стандарте CSMA/CD LAN анализируются с использованием аппроксимации модифицированной диффузией (MDA), которая достигает достаточно хорошей точности в относительно простых вычислениях.

Поскольку точного аналитического решения для современной многоканальной системы транспортировки GI/G/s до настоящего времени еще не получено, то применяют модель диффузии функции плотности распределения. Известно, что процесс диффузии представляет собой Марковский процесс непрерывных состояний непрерывного времени. Для устойчивого состояния определяют аппроксимированное действительное число вызовов, присутствующих в системе во время t, решая известное уравнение диффузии. Поскольку неизвестные параметры полагают равными SCVs времени обслуживания и промежутков времени между вызовами, то это предполагает наличие тяжелых условий нагрузки и в силу этого низкой точности.

Согласно методу MDA неизвестные параметры определяются путем сравнения результатов аппроксимации диффузией с точными решениями для однолинейных систем M/G/1 и GI/M/1. И хотя модифицированные параметры были определены для s = 1, они не включают s явно.

Отсюда можно расширить аппроксимацию до многоканальной системы GI/G/s, достигнув приемлемой точности результата: среднего времени ожидания и среднего числа ожидающих вызовов.