Вычисление двойного интеграла в полярных координатах

Для упрощения вычисления двойного интеграла часто применяют метод подстановки (как это делалось и при вычислении определенного интеграла), т. е. вводят новые переменные под знаком двойного интеграла.

Определим преобразование независимых переменных х и у (замену переменных) как

Если функции (7.9) имеют в некоторой области D* плоскости Ouv непрерывные частные производные первого порядка и отличный от нуля определитель

а функция ƒ(х;у) непрерывна в области D, то справедлива формула замены переменных в двойном интеграле:

Функциональный определитель (7.10) называется определителем Якоби или якобианом (Г.Якоби - немецкий математик). Доказательство формулы (7.11) не приводим.Рассмотрим частный случай замены переменных, часто используемый при вычислении двойного интеграла, а именно замену декартовых координат х и у полярными координатами r и j.

В качестве u и υ возьмем полярные координаты r и j. Они связаны с декартовыми координатами формулами х=rcos j, у=r sin j (см. Часть 1, п. 9.1).

Правые части в этих равенствах - непрерывно дифференцируемые функции. Якобиан преобразования определяется из (7.10) как

Формула замены переменных (7.11) принимает вид:

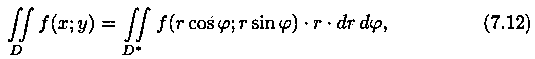
где D* - область в полярной системе координат, соответствующая области D в декартовой системе координат

.

Для вычисления двойного интеграла в полярных координатах применяют то же правило сведения его к двукратному интегралу. Так, если область D* имеет вид, изображенный на рисунке 10 (ограничена лучами j=а и j=β, где а < β, и кривыми r=r1(j) и r=r2(j), где r1(j)≤r2(j), т. е. область D* правильная: луч, выходящий из полюса, пересекает ее границу не более чем в двух точках), то правую часть формулы (7.12) можно записать в виде

Внутренний интеграл берется при постоянном j.

Замечания.

1. Переход к полярным координатам полезен, когда подынтегральная функция имеет вид ƒ(х2+у2); область D есть круг, кольцо или часть таковых.

2. На практике переход к полярным координатам осуществляется путем замены х=rcos j, у=rsin j, dxdy=r dr dj; уравнения линий, ограничивающих область D, также преобразуются к полярным координатам. Преобразование области D в область D* не выполняют, а, совместив декартову и полярную системы координат, находят нужные пределы интегрирования по r и j (исследуя закон изменения r и j точки (r; j) при ее отождествлении с точкой (х; у) области D).

Пример 7.2. Вычислить где область D - круг

Решение: Применив формулу (7.12), перейдем к полярным координатам:

Область D в полярной системе координат определяется неравенствами (см. рис. 11) 0≤j≤2p,0≤r≤3. Заметим: область D - круг - преобразуется в область D* - прямоугольник. Поэтому, согласно формуле (7.13), имеем:

Приложения двойного интеграла

Приведем некоторые примеры применения двойного интеграла.

Объем тела

Как уже показано (п. 7.2), объем цилиндрического тела находится по формуле

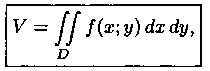
где z=ƒ(х;у) - уравнение поверхности, ограничивающей тело сверху.

Площадь плоской фигуры

Если положить в формуле (7.4) ƒ(х;у)=1, то цилиндрическое тело «превратится» в прямой цилиндр с высотой Н=1. Объем такого цилиндра, как известно, численно равен площади S основания D. Получаем формулу для вычисления площади S области D:

или, в полярных координатах,

ТРОЙНОЙ ИНТЕГРАЛ

Основные понятия

Обобщением определенного интеграла на случай функции трех переменных является так называемый «тройной интеграл».

Теория тройного интеграла аналогична теории двойного интеграла. Поэтому изложим ее в несколько сокращенном виде.Пусть в замкнутой области V пространства Oxyz задана непрерывная функция u=ƒ(х;у;z). Разбив область V сеткой поверхностей на n частей и выбрав в каждой из них произвольную точку Мi(хi;yi;zi), составим интегральную суммудля функции ƒ(х; у; z) по

области V (здесь ∆Vi - объемэлементарной области Vi).

Если предел интегральной суммы существует при неограниченном увеличении числа n таким образом, что каждая «элементарная область» Vi стягивается в точку (т. е. диаметр области di стремится к нулю, т. е. di-> 0), то его называют тройным интегралом от функции u=ƒ(х;у;z) по области V и обозначают

Таким образом, по определению, имеем:

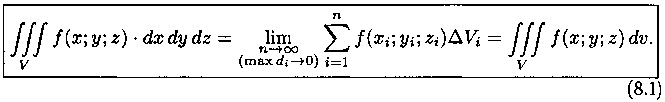
Здесь dv=dx dy dz - элемент объема.

Теорема 8.1 (существования). Если функция u=f(x;y;z) непрерывна в ограниченной замкнутой области V, то предел интегральной суммы (8.1) при n->∞ и max di -> 0 существует и не зависит ни от способа разбиения области V на части, ни от выбора точек Mi(xi,yi,zi) в них.

Тройной интеграл обладает теми же свойствами, что и двойной интеграл:

1.

2.

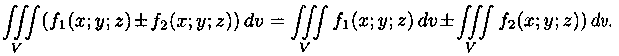
3.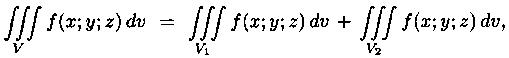 если V=V1 È V2, а пересечение V1 и V2 состоит из границы, их разделяющей.

4. если в области V функция f(x;y;z)>=0. Если в области интегрирования ƒ(х;у;z)>=j(x;y;z), то и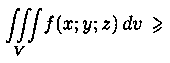

5 .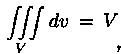 , так как в случае любая интегральная сумма имеет вид и численно равна объему тела.

6. Оценка тройного интеграла:

где m и М - соответственно наименьшее и наибольшее значения функции f(x;y;z) в области V.

7. Теорема о среднем значении: если функция f(x;y;z) непрерывна в замкнутой области V, то в этой области существует такая точка Mo(xo;yo;zo), что

где V - объем тела.