Вопрос №18(19): Длина дуги кривой.

1. Понятие простой кривой;

2. Понятие спрямляемой прямой;

3. Длина дуги;

4. Достаточное условие спрямляемости кривой;

5. Формула для вычисления длины дуги.

Пусть на заданы две непрерывные функции и Множество {M} точек при называется кривой на плоскости xy.

Определение: Множество {M} всех точек М, координаты x и y которых определяются уравнениями и при называется простой плоской кривой L, если различным значениям параметра t из отвечают различные точки множества {M}.

В этом случае говорят прямая параметризована уравнениями.

Определение: Уравнения и , , где и непрерывные функции на промежутке определяют непрерывную прямую, заданную при помощи параметра t.

Определение: Непрерывная прямая называется гладкой, если и имеют непрерывные производные на и выполняется неравенство:

Можно показать, что в каждой точке гладкой кривой существует касательная к графику функции ( в том числе и касательные, параллельные осям координат ).

Пусть плоская кривая L параметризуется уравнениями

Произведем произвольное разбиение точками a=t₀<t₁<…<t_n=b. Обозначим М₀, М₁, … , М_n соответствующие точки кривой с координатами:

Пусть L(t)=М₀, М₁, … , M_n – ломанная, вписанная в кривую L, отвечающая данному разбиению, Длина звена ломаннной:

Определение: Кривая L называется спрямленной (имеющеей длину), если множество длин вписанных в прямую L ломанных l, отвечающих всевозможным разбиениям отрезка называется длиной дуги L и обозначается:

{t_k}

Замечание: если кривая L спрямляема, то длина ее дуги не зависит от параметризации этой кривой.

Замечание: понятие длины дуги пространственной кривой, заданной параметрическими уравнениями , ,

z=(t), где t, (2) вводится так же, как и понятие длины дуги плоской кривой. Длина ломаной вписанной в пространственную кривую будет равна:

Пространственная кривая определяемая уравнениями (2), называется спрямляемой, если l длин ломаных вписанных в кривую ограничено сверху. Точная верхняя грань этого множества и называется длиной дуги.

Уравнения (2) определяют кривую как геометрическое место точек, а также определяют ориентацию этой кривой, т.е. направление возрастания параметра.

Достаточное условие:

Теорема: Пусть функция х=(t), и y=t), непрерывна и имеет непрерывные первые производные на отрезке . Тогда кривая L, определяемая уравнениями (1) спрямляема и длина ее дуги может быть вычислена по формуле:

Замечание: если кривая L является графиком функции y=f(x), которая непрерывна и имеет непрерывные производные на , то прямая спрямляема, то длина ее дуги может быть вычислена по формуле:

Если прямая L определяется полярными уравнениями  где ₁₂, а функция  непрерывна и имеет непрерывную производную, то длина ее дуги вычисляется по формуле:

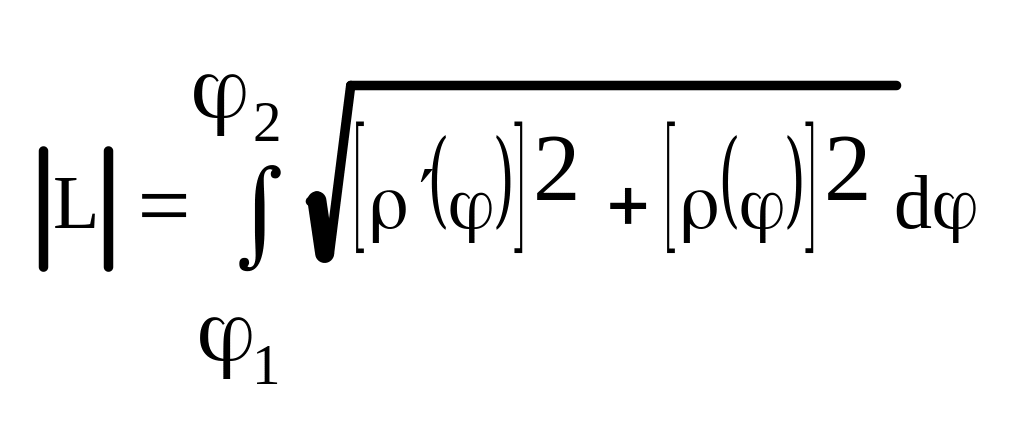
Вопрос №20: ДИФФЕРЕНЦИАЛ ДЛИНЫ ДУГИ

Пусть функции х=t), y=(t) непрерывна вместе со своими производными на а,b переменная длина дуги:

Умножим на dt:

Тогда:

xa,b

Вопрос №21: ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА

Приближенное вычисление основано на определении интеграла.

Метод прямоугольников

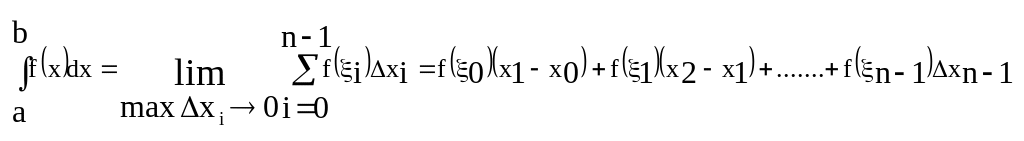
Берем левый конец за _i, тогда:

(1)

Берем правый конец за _i, тогда:

(2)

Берем середину за _i, тогда:

; ;

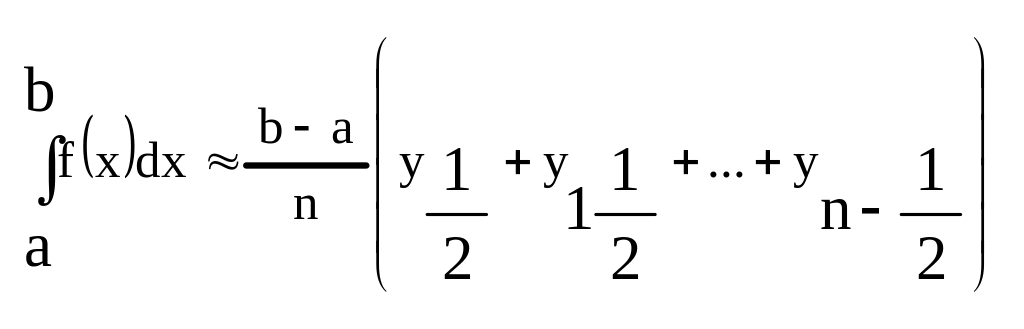(3)

Приближенное интегрирование, основанное на интерполировании

Простейшая формула основанная на линейной интерполяции получается как среднее арифметическое формул (1) и (2).

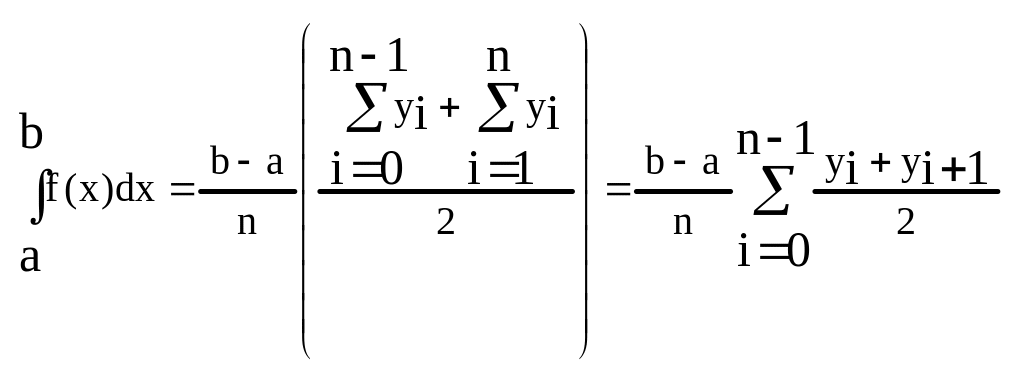(4) – формула трапеции

где М₂ =

Формула Симпсона

Сущность метода парабол заключается в следующем: отрезок [a, b] делится на 2n равных частей и пусть точки деления a=x₀<x₁<…<x_2n=b. Соответствующие значения функции записываем y₀, y₁, …, y_2n на [a, b]. Проведем квадратичную интерполяцию данной подинтегральной функции на [x₀, x₂] с узлами интерполяции x₀, x₁, x₂. Заменим для этого функцию y=f(x) на данном участке интерполяционным полиномом Ньютона:

y₀ = y₁ – y₀

тогда

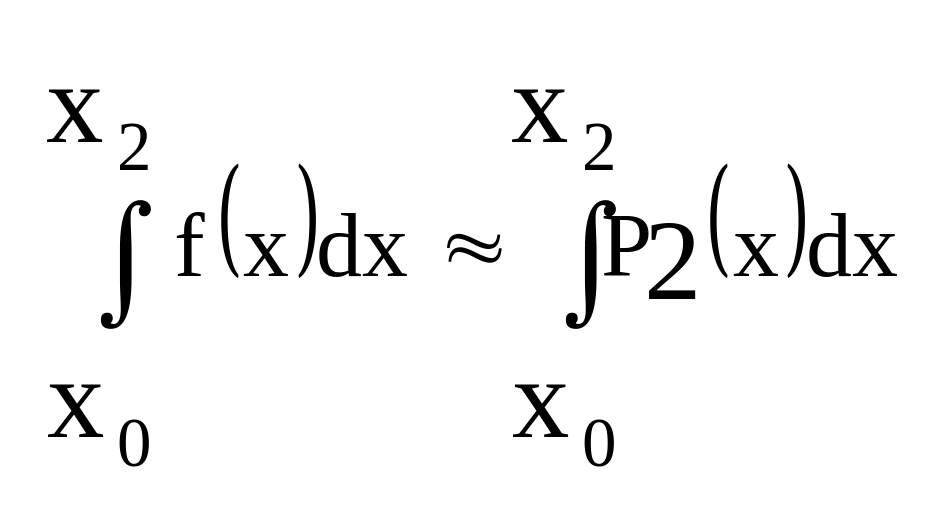
Проведя аналогичные вычисления на каждом из промежутков, и складывая почленно формулы получим приближенную формулу для вычисления интегралов – формулу Симпсона (формулу парабол):

или