Вопрос №11

1. Интегралы вида:

;

где: r1,…..rs – постоянные рациональные числа.

Определитель

Подынтегральная функция моет быть представлена как рациональная функция от др. переменной.

Пусть m – общий знаменатель чисел r1,…..rs ,

Pi – целое,

Положим

- рациональная функция.

- тоже рациональная функция

То есть интеграл (п.1) сводится к интегралу рациональной дроби.

Чтобы найти выражение для исходного И, надо после вычисления интеграла сделав обратную перемену вернуться к старой переменной х

Рассмотрим частные случаи:

, где m – общее значение дробей.

Пример:

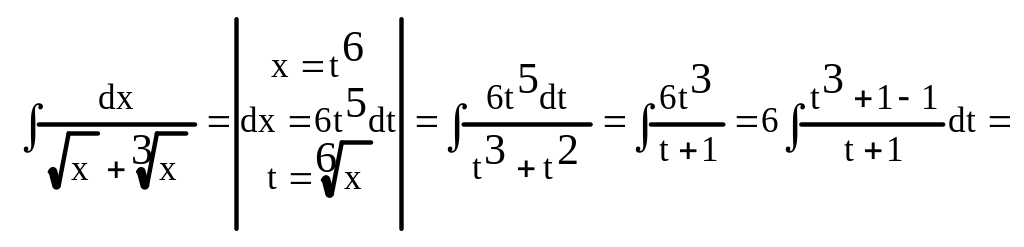
Пример:

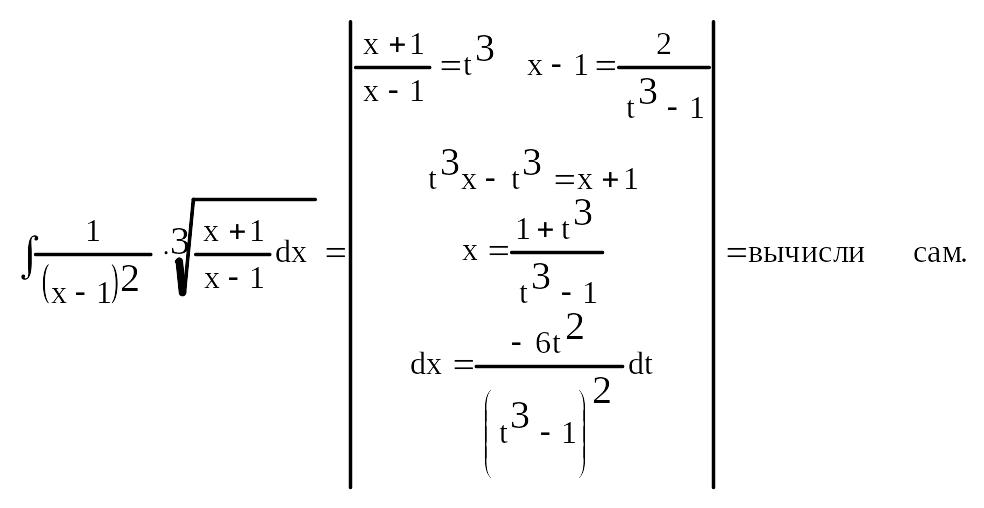
Вопрос №12

2. Интегралы вида:

Интегралы от таких функций сводятся к интегралам от рациональных функций с помощью специальной подстановки, которая называется подстановками Эйлера.

Однако обычно эти подстановки приводят к громоздким вычислениям, поэтому их надо применять только в крайних случаях.

Вообще говоря заметим, что:

Нетрудно увидеть, что интеграл в случае, когда подкоренное выражение положительно с помощью линейной подстановки может быть приведено к 1 из 3:

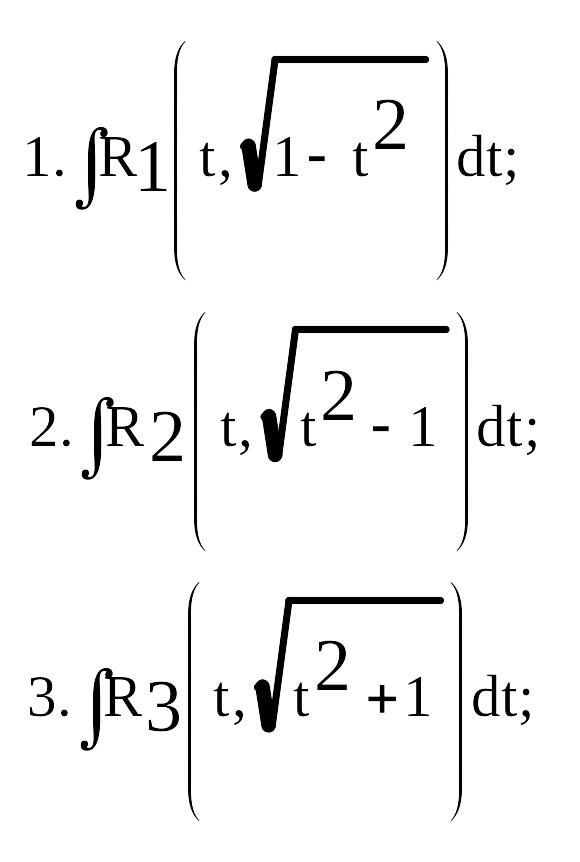
Для вычисления этих интегралов часто удобно применять тригонометрические подстановки:

Пример:

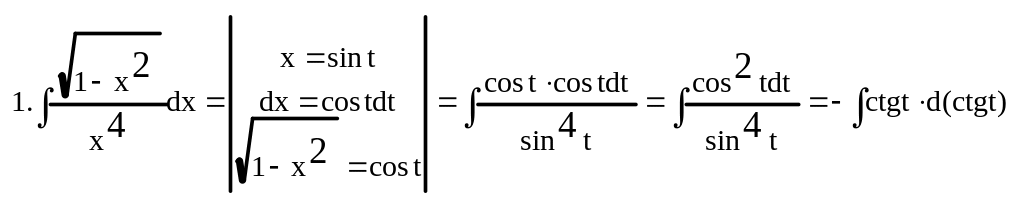
Вопрос№13.

Интегрирование трапе……………… (тригонометрических) функций.

Рационализация этого интегрирования достигается с помощью подстановки:

Интеграл от рациональной функции берётся.

Рассмотрим частные случаи:

В данном случае используется: sinx=t

Иногда полезно прибегать к другим приемом:

Пример:

Тема №2 Определенный интеграл.

2_1;2_2Задачи приводящие к понятию определенного интеграла (ОИ) и его определению.

1. Зададим на отр. [a,b] а,b – локальные числа, …………….. ……………. И непрерывную функцию f(x)

Поставим задачу: требуется определить понятие площади фигуры ограниченной кривой y=f(x), осью Х и прямыми х=а, х=b

Произведем разбиение отрезка АB на n – частей точками

Выберем на каждом из полученных частичных отрезков [xi, xi+1], i=0, по произвольной точке

Определим значения функции f(x) в этих m. и составим сумму:

интегральная сумма (равна сумме площадей прямоугольников с высотой и основание )

где:

Устремим , притом так чтобы max частичный отрезок разбиение стремится к нулю. Если при этом, величена к определённому пределу S, независящему от способа разбиения и выбора точек , то эту величину называют – площадью криволинейной фигуры.

2.

Дан линейный неоднородный стержень, лежащий на оси Ох в пределах отрезка AB. Требуется определить массу этого стержня.

Путсь плотность распределения массы, этого стержня есть непрерывная функция

Для определения массы стержня разобьем на n – производных отрезков точками в пределах каждого частного отрезка выберем произвольную точку т.к. в пределах частного отрезка [xi, xi+1] функция изменяется мало то массу части стержня, соответствующего отрезка [xi, xi+1] можно считать приближенно равной:

Массу же всего стержня приближенно будет ровна:

Такое значение массы очевидно будет равна:

Определение:

Пусть на [a,b] на части , произвольными точками и будем говорить, что этим произведено разбиение R[a,b]. На каждом частичном отрезке разбиения выберем произвольно т. и составим сумму:

называемую интегральной суммой функции f(x) соответствующей разбиению R.

Обозначим через

Максимальную длину частичных отрезков разбиения R.

Предел (если он существует) к которому стремиться интегральная сумма , от функции f(x) когда называется определенным интегралом от функции f(x) на [a,b] и обозначается следующим образом:

Число: a – нижний предел;

b – верхний предел;

Определение 1:

ОИ от функции f(x) на [a,b], называется число I, удовлетворяющие следующему свойству:

для всякого найдется число Б что модуль разности:

Для любого разбиения R[a,b] у которого меньше при любом (выборе точек )

Замечание: - данной определение может быть приложено только ограничительным функциям

Имеет место теорема:

Если функция интегрируема на [a,b] , то она ограничена на этом отрезке

Условие ограниченности функции, необходимое , но недостаточное для интегрируемости

Функция Дирикия

функция ограничена.