
- •Теория электромагнитного поля. Уровнения Максвелла.
- •2) Физическая природа электрического тока
- •5) Источники электрической энергии в цепи постоянного тока
- •6) Второй закон
- •Первый закон Кирхгофа
- •9)Метод Контурных Токов
- •9)Метод контурных токов (гармонический ток)
- •10) Метод узловых потенциалов.
- •12) Метод эквивалентного генератора
- •14) Эквивалентные преобразования пассивных электрических цепей.
- •15) Эквивалентное преобразование «Звезда – треугольник»
- •22) Электрический ток в активном сопротивлении.
- •Закон Ома для переменного тока
- •23) Электрический ток в индуктивности.
- •25) Последовательное соединение r, l, c
- •27) Последовательное соединение r, l, c
- •27) Параллельное соединение r, l, c
- •29) Мощность в цепи переменного тока.
- •31)Мощность цепи переменного тока.
- •31)Мощность цепи переменного тока.
- •33) Резонанс напряжений: условия возникновения, резонансная частота, волновое сопротивление, добротность, векторная диаграмма.
- •35) Взаимная индукция. Коэффициент связи.
- •40) Что такое трансформатор
- •45,46) Логарифмические частотные характеристики
12) Метод эквивалентного генератора
При расчёте сложной электрической цепи приходится выполнять значительную вычислительную работу даже в том случае, когда требуется определить ток в одной ветви. Объём этой работы в несколько раз увеличивается, если необходимо установить изменение тока, напряжения, мощности при изменении сопротивления данной ветви, так как вычисления нужно производить несколько раз, задаваясь различными значениями сопротивления.
В любой электрической схеме можно мысленно выделить какую-то одну ветвь, а всю остальную часть схемы, независимо от структуры и сложности, условно изобразить прямоугольником, который представляет собой так называемый двухполюсник.
Таким образом, двухполюсник - это обобщённое название схемы, которая двумя выходными зажимами (полюсами) присоединена к выделенной ветви. Если в двухполюснике есть источник Э.Д.С. или тока, то такой двухполюсник называют активным. Если в двухполюснике нет источника Э.Д.С. или тока, то его называют пассивным.
При решении задачи методом эквивалентного генератора (активного двухполюсника) необходимо:
1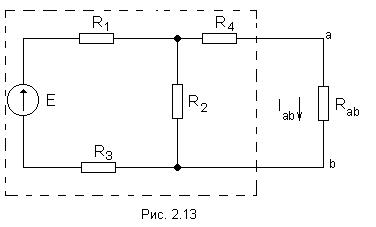 )
Мысленно заключить всю схему, содержащую
Э.Д.С. и сопротивления, в прямоугольник,
выделив из нее ветвь аb, в которой
требуется найти ток (рис 2.13).
)
Мысленно заключить всю схему, содержащую
Э.Д.С. и сопротивления, в прямоугольник,
выделив из нее ветвь аb, в которой
требуется найти ток (рис 2.13).
2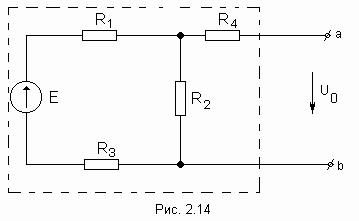 )
Найти напряжение на зажимах разомкнутой
ветви ab (в режиме
холостого хода).
)
Найти напряжение на зажимах разомкнутой
ветви ab (в режиме
холостого хода).
Напряжение холостого хода Uо (эквивалентное Э.Д.С. Еэ) для рассматриваемой цепи
можно найти так:
![]()
Сопротивление R4 в расчёт не вошло, так как при разомкнутой ветви ab ток по нему не протекает.
3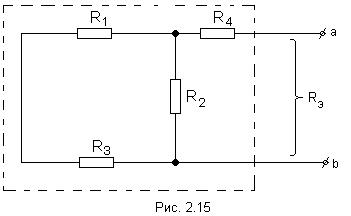 )айти
эквивалентное сопротивление. При этом
источники Э.Д.С. закорачиваются, а ветви,
содержащие источники тока, размыкаются.
Двухполюсник становится пассивным.
)айти
эквивалентное сопротивление. При этом
источники Э.Д.С. закорачиваются, а ветви,
содержащие источники тока, размыкаются.
Двухполюсник становится пассивным.
Для
данной схемы
![]() 4) числить значение тока. Для данной
схемы имеем:
4) числить значение тока. Для данной
схемы имеем:
![]()
Метод эквивалентного генератора.
При расчете тока в одной из ветвей разветвленной цепи, содержащей произвольное число источников и потребителей, удобно рассматривать цепь, состоящую из двух частей: искомой ветви и остальной части. По отношению к рассматриваемой ветви вся остальная часть цепи является активным двухполюсником, и задача заключается в определении тока или напряжения на зажимах активного двухполюсника при подключении к нему потребителя с сопротивлением R..
Согласно II закону Кирхгофа ток не изменится, если в цепь, образованную активным двухполюсником и потребителем, включить последовательно два идеализированных встречно направленных источника с одинаковыми ЭДС (рис. 2.10). Величину каждой из них выбираем совпадающей с напряжением UХХ на зажимах активного двухполюсника в режиме холостого хода, который имеет место при отключенном потребителе.
![]() (2.16)
(2.16)
Ток I в цепи с двумя источниками определим методом наложения. С этой целью источники разбиваем на две группы:
1. Источники активного двухполюсника и Е1, которые сохраняются в подсхеме.
Согласно II закону Кирхгофа:
![]() поскольку
поскольку
![]() .
.
2. все потребители активного двухполюсника и Е2, сохраняются в подсхеме на рис. 2.12.

Если эквивалентное сопротивление пассивного двухполюсника, образованного коротким замыканием источников ЭДС и обрывом ветвей, содержащих источники тока, обозначить через Rвх, получим простую одноконтурную схему (рис. 2.13), которую можно рассчитать по закону Ома:
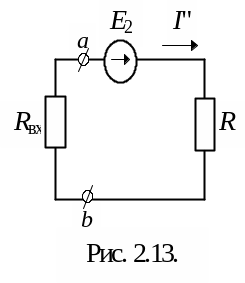
![]() Эта формула отражает теорему
об активном двухполюснике или
об эквивалентном источнике напряжения:
относительно любой ветви разветвленной
электрической цепи вся остальная часть
схемы может быть представлена как
источник напряжения, ЭДС которого равна
UXX,
а внутренне сопротивление равно Rэкв.
Эта формула отражает теорему
об активном двухполюснике или
об эквивалентном источнике напряжения:
относительно любой ветви разветвленной
электрической цепи вся остальная часть
схемы может быть представлена как
источник напряжения, ЭДС которого равна
UXX,
а внутренне сопротивление равно Rэкв.
При коротком замыкании ветви с нагрузкой R = 0 ток превращается в ток короткого замыкания:
![]() Параметры
активного двухполюсника можно определить
опытным путем. Для этого необходимо
разомкнуть i-ую
ветвь и измерить
Параметры
активного двухполюсника можно определить
опытным путем. Для этого необходимо
разомкнуть i-ую
ветвь и измерить
![]() ,
затем замкнуть накоротко Ri
и измерить IКЗ
:
,
затем замкнуть накоротко Ri
и измерить IКЗ
: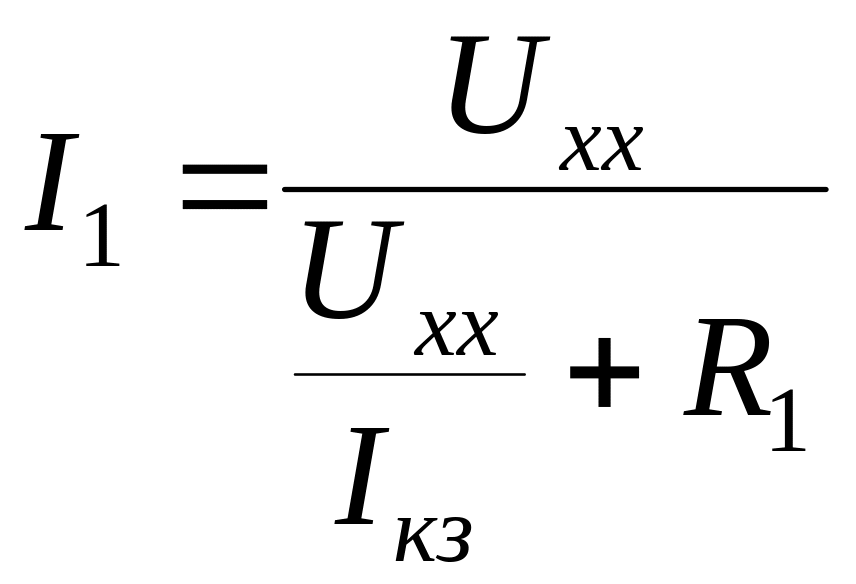 Методика
расчета линейной электрической цепи
методом эквивалентного генератора:
Методика
расчета линейной электрической цепи
методом эквивалентного генератора:
Отключается потребитель в ветви с искомым током и на зажимах обозначается UXX по направлению тока.
В образовавшейся более простой цепи находится Uõõ с помощью II закона Кирхгофа, записанного для любого контура, содержащего Uхх. Токи в ветвях упрощенной схемы определяются любым известным методом.
Определяется Rвх на зажимах разомкнутой ветви при условии E=0 и J=0. В полученной пассивной цепи пользуются правилами эквивалентных преобразований для потребителей.
По найденным Uõõ и Rвх определяется ток в искомой ветви, значение которого может быть и отрицательным.
Замечание
1: Rвх
можно найти по формуле
![]() IКЗ
при условии Ri=0
любым известным методом.
IКЗ
при условии Ri=0
любым известным методом.
Замечание 2: если ветвь, в которой определяется ток, содержит источник ЭДС, следует данный источник отнести к активному двухполюснику, отключив только сопротивление Ri. Тогда величина E войдет в расчет UXX .
13)
