33) Резонанс напряжений: условия возникновения, резонансная частота, волновое сопротивление, добротность, векторная диаграмма.

Резонанс напряжений наблюдается в последовательных цепях. Рассмотрим режим резонанса напряжений для последовательной RLC-цепи.

Для схемы на рис. 4.1 справедливо

. (4.1)

Изменим частоту генератора или параметры катушки индуктивности или емкости так, чтобы для этой схемы было , тогда напряжение на входе , т.е. ток и напряжение на входе совпадают по фазе. В цепи – режим резонанса:

.

Частота, при которой наблюдается резонанс, может быть определена из соотношения

.

Т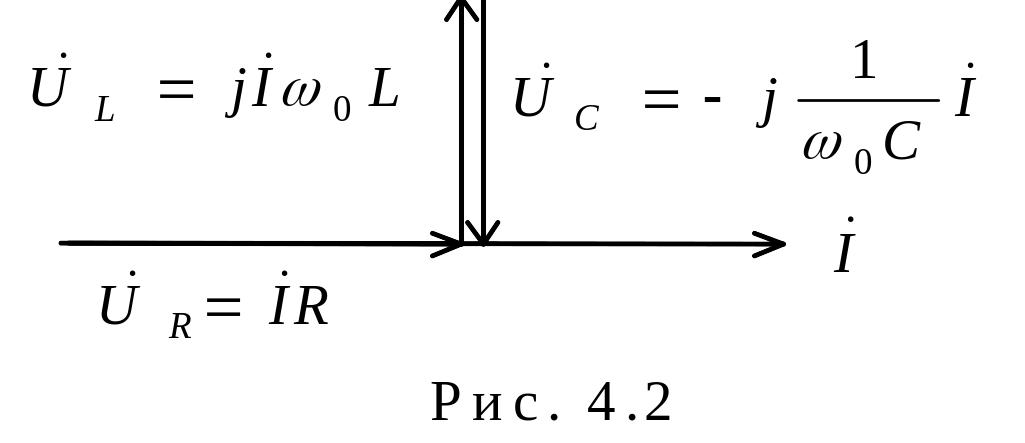 ок в цепи в режиме резонанса

т.е. максимально возможный при данных параметрах контура.

Полная мощность цепи , т.е. равна мощности, выделяемой на активном сопротивлении.

В каждый момент времени . Учитывая, что , получаем

где  – характеристическое, или волновое сопротивление резонансного контура, измеряемое в омах.

Отношение напряжения на реактивных элементах ( и ) к напряжению на входе в режиме резонанса называют добротностью контура:

. (4.5)

Чем больше и чем меньше активное сопротивление в цепи, тем выше напряжение на реактивных элементах по сравнению с напряжением на входе контура.

34)Рассмотрим цепь с двумя параллельными ветвями на рис. 3.22.

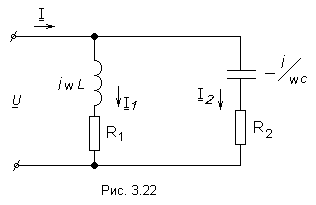
Такую цепь часто называют параллельным контуром. Условием возникновения резонанса является равенство реактивных проводимостей:

, (3.57)

. (3.58)

. (3.59)

При противоположные по фазе реактивные составляющие токов равны, поэтому резонанс в рассматриваемой цепи получил название резонанса токов.

Из векторной диаграммы на рис. 3.23а видно, что при резонансе ток на выходных выводах контура может быть значительно меньше токов в отдельных ветвях.

При резонансе общий ток в параллельном контуре по фазе совпадает с приложенным напряжением.

Добротность контура показывает во сколько раз ток в ветви превышает питающий ток и определяется следующим соотношением:

, (3.60)

где ,

- эквивалентное активное сопротивление при резонансе:

- если . (3.61)

В общем случае резонансная частота определяется по формуле:

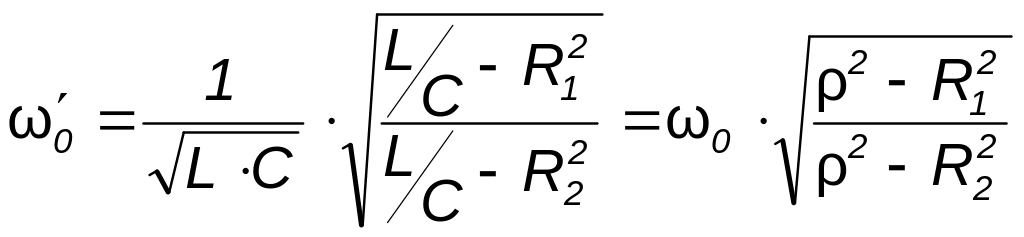, (3.62)

где - резонансная угловая частота при - аналогичная последовательному контуру.

В теоретическом случае при токи и сдвинуты по фазе относительно напряжения на углы (рис. 3.23б) и суммарный ток . Входное сопротивление цепи при этом бесконечно велико.

Как видно из формулы 3.62 резонанс возможен, если сопротивления оба больше или оба меньше ρ.

Если , то резонансная частота имеет любое значение, то есть резонанс наблюдается на любой частоте.

Н а рис. 3.24 показаны частотные характеристики проводимостей ветвей и , и входной проводимости цепи .

При изменении частоты от 0 до эквивалентная проводимость , то есть индуктивная и изменяется от до 0. При наступает резонанс токов, .

При возрастании частоты от до входная проводимость , то есть имеет емкостной характер и изменяется от 0 до .