26.Теорема об общем решении неоднородных слау( с доказательством).Следствие

Пусть тогда:

Если , где — число переменных системы, то решение существует и оно единственно;

Если , то общее решение системы имеет вид , где

— общее решение однородной системы, называемое общим однородным решением,

— частное решение неоднородной системы, называемое частным неоднородным решением.

Неоднородной системой линейных уравнений называется система вида:

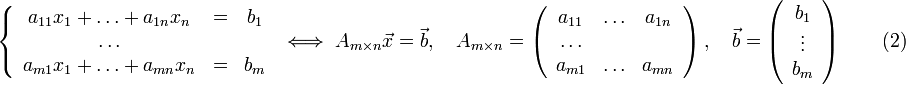
27+28. Определение линейного пространства Определение:

Линейное пространство (ЛП) – совокупность произвольных объектов, на которых введены две абстрактные операции, условно именуемые сложением (+) и умножением на число (λ).

Элементы линейного пространства будем называть векторами.

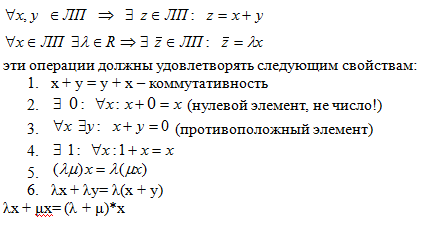29. Определение ЛНЗ и ЛЗ элементов ЛП.Примеры ЛНЗ элементов в различных ЛП.Свойства ЛЗ и ЛНЗ элементов ЛП. Определение. Система векторов векторного пространства, которая представляет нулевой вектор ТОЛЬКО тривиально называется линейно независимой.

Определение. Система векторов векторного пространства, которая может представить нулевой вектор нетривиально называется линейно зависимой. Свойства:  1. Любая система векторов e1,e2, ..., ek линейного пространства, содержащая нулевой вектор, линейн зависима.

2. Любая система векторов e1,e2, ..., ek линейного пространства, содержащая пару взаимно противоположных векторов, линейн зависима.

3. Любая подсистема векторов линейно независимой системы векторов линейного пространства линейно независима.

4. Любая система векторов линейного пространства, содержащая линейно зависимую подсистему векторов, линейно зависима.

5. Система векторов линейного пространства линейно зависма тогда и только тогда, когда хотя бы один из векторов системы линейно выражается через остальные векторы системы (представлен в виде разложения по векторам системы).

6. Система векторов линейного пространства линейно независма любая её подсистемы векторов.

6. Система векторов, состоящая из одного ненулевого вектора линейного прострранства, линейно независима.

Примеры: 1) Система векторов ·i, j линейного пространства R2 геометрических радиусов векторов плоскости линейно независима.Действительно.

i = (1, 0),  j = (0, 1),   С1·i + С2· j = (С1, С2), а из (С1, С2) = 0 следует, что  С1 = 0 и С1 = 0, т.е. система векторов i, j из R2 линейно независима.

2) Система, состоящая из одного нулевого вектора линейного пространства линейно зависма.

     Действительно, равенство С1·0 = 0 справедливо при любом значении коэффициента С1, например, при С1 = 1 ≠ 0.

30. Определение базиса ЛП.Единственность разложения элемента пространства по базису( с док-ом).Координаты элемента ЛП.

Базис векторного пространства – это упорядоченная совокупность линейно независимых векторов этого пространства, число которых равно размерности пространства.

Любой вектор этого линейного пространства можно представить как сумму элементов данного базиса, умноженных на некоторые числа. Эти числа однозначно определены базисными векторами и данным вектором, поэтому она называются координатами вектора в данном базисе. Любой вектор векторного пространства можно разложить по его базису и притом единственным способом. 31. Размерность пространства. Теорема о связи базиса и разложение пространства ( с док-ом). Определение. Размерностью векторного пространства называется число, равное максимальному количеству линейно независимых векторов в этом пространстве.

Замечания.

• Размерность пространства, состоящего только из одного нулевого вектора, равна нулю. Такое пространство называется тривиальным.

• Если в линейном пространстве существует любое число линейно независимых векторов, то такое пространство называется бесконечномерным. Мы будем рассматривать, в основном, конечномерные линейные пространства. Бесконечномерные пространства являются предметом специального изучения.

Теорема о связи базиса и разложение пространства ( с док-ом).

Любой вектор n-мерного векторного пространства единственным образом раскладывается по базису.

Доказательство.

Пусть - базис n-мерного векторного пространства. Добавим к этим векторам n-мерный вектор x. Тогда полученная система векторов будет линейно зависимой и вектор x может быть линейно выражен через векторы : , где - некоторые числа. Так мы получили разложение вектора x по базису. Осталось доказать, что это разложение единственно.

Предположим, что существует еще одно разложение , где - некоторые числа. Отнимем от левой и правой частей последнего равенства соответственно левую и правую части равенства :

Так как система базисных векторов линейно независима, то по определению линейной независимости системы векторов полученное равенство возможно только тогда, когда все коэффициенты равны нулю. Поэтому, , что доказывает единственность разложения вектора по базису.

32. Определение линейного подпространства.Примеры ЛПП.Утверждение о том, что ЛПП является ЛП Линейное подпространство или векторное подпространство Непустое подмножество линейного пространства называется подпространством, если для любых векторов и .

33. Утверждение о размерности подпространства Число элементов (мощность) максимального линейно независимого подмножества пространства не зависит от выбора этого подмножества и называется рангом, или размерностью, пространства, а само это подмножество— базисом Элементы базиса также называют базисными векторами. 34. Определение линейного оператора.Свойства ЛО.Примеры ЛО Линейным оператором, действующим из пространства H в пространство H1 называется отображение ,удовлетворяющее условию

для любых чисел и и любых векторов x и y пространства H. Оператор I называется единичным или тождественным.

Существует также и нолевой оператор. Общие свойства линейных операторов.

1). Если и -- линейные операторы, то для любых чисел и отображение ,заданное формулой

является линейным оператором.

Если ,то формула (2) определяет операцию умножения оператора A на число ,а если , то -- операцию сложения операторов A и B. Легко видеть, что эти операции превращают множество всех линейных операторов, действующих из H в H1, в линейное пространство (см. задачу 2). При этом нулевым ``вектором'' будет нулевой оператор, а ``вектором'', противоположным ``вектору'' A будет оператор -A.

2). Если и -- линейные операторы, то отображение BA, действующее из H в H2, и заданное с помощью формулы

(BA)x=B(Ax),

является линейным оператором и называется произведением операторов A и B. 35. Матрицы ЛО.Утверждение о матрице ЛО(с дак-ом) Матрицей линейного оператора в базисах e, f называется матрица A, столбцами которой являются координаты образов базисных векторов базиса e в базисе f , A = {aij}= {A(ej )i}:

Утверждение. Если матрица осуществляет действие оператора А, то В является матрицей оператора А.

Доказательство. в базисе

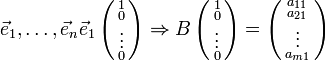
первый столбец В совпадает с первым столбцом , аналогично все остальные тоже совпадают

36. Связь координат образа и прообраза ЛО Теорема. (связь координат образа и прообраза). Если в пространстве Rn определен некоторый базис, и — векторы (столбцы) из Rn и , то векторы-столбцы их координат в этом базисе связаны соотношением , где A — матрица оператора A в этом же базисе.

37. Матрицы перехода от старого базиса к новому.Связь координат одного и того же элемента в разных базисах.(с док-ом) Ма́трицей перехо́да от базиса к базису является матрица, столбцы которой — координаты разложения векторов в базисе .