
- •1. Матрицы ,сложение матриц, свойства.
- •2.Матрицы. Умножение матриц. Коммутирующие матрицы.
- •3.Ассоциативность умножение матриц. Теорема с доказательством.
- •4.Определение транспонирующей матрицы. Св-ва трансонпонир. Матрицы с док-вом.
- •5. Перестановки из n элементов. Порядок, инверсия. Определение четности перестановки. Транспозиция (утв. 1 и следствия)
- •6. Утверждение об изменении четности перестановки(с док-вом). Следствие 1, следствие2( с док-вом).
- •7.Опред. Определителя. Св-ва определителя(с док-вом).
- •8. Лемма о знаке члена определителя(с док-вом)
- •9. Опред. Mij,Aij, Лемма(с док-вом)
- •10.Теорема о разложении определителя по эллементам строки, столбца (с док-вом). Следствие (без док-ва). Формула Бине-Коши.
- •11. Определение Линейно Независимых и Линейно Зависимых столбцов. Св-ва лз(лнз) столбцов (с док-вом).
- •12. Критерий лз столбцов (с док-вом)
- •13. Минор матрицы. Ранг м-цы. Базисный минор. Теорема о базисном миноре ( с док-вом)
- •15. Теорема о ранге матрицы (с док-вом).
- •16. Методы вычисл. Ранга м-цы. Утверждение о приведении матрицы к трапец. Форме (с док- вом).
- •17. Определение обратной м-цы, теорема о существовании обратной матрицы (с док-вом).
- •18. Свойства обратных матриц
- •19. Слау. Основные понятия
- •20. Теорема Крамера
- •21. Элементарное преобразование функций слау. Метод Гаусса. Решение слау.
- •26.Теорема об общем решении неоднородных слау( с доказательством).Следствие
- •38.Связь матриц ло в разных базисах( с док-ом)
20. Теорема Крамера
Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы.
Пример
Система линейных уравнений:

Определители:
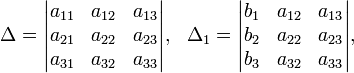
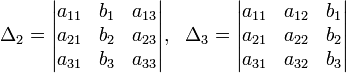
Решение:
![]()
21. Элементарное преобразование функций слау. Метод Гаусса. Решение слау.
Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц. Таким образом, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.
Элементарными преобразованиями строк называют:
перестановка местами любых двух строк матрицы;
умножение любой строки матрицы на константу , ;
прибавление к любой строке матрицы другой строки.
Пример
Покажем, как методом Гаусса можно решить следующую систему:
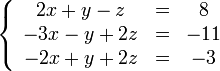
Чтобы ее решить, нужно сделать нули под главной диагональю системы
Обнулим коэффициенты
при
![]() во
второй и третьей строчках. Для этого
вычтем из них первую строчку, умноженную
на
во
второй и третьей строчках. Для этого
вычтем из них первую строчку, умноженную
на
![]() и
и
![]() ,
соответственно:
,
соответственно:
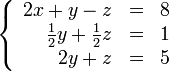
Теперь обнулим
коэффициент при
![]() в
третьей строке, вычтя из неё вторую
строку, умноженную на
в
третьей строке, вычтя из неё вторую
строку, умноженную на
![]() :
:

В результате мы привели исходную систему к треугольному виду, тем самым закончив первый этап алгоритма.
На втором этапе разрешим полученные уравнения в обратном порядке. Имеем:
![]() из третьего;
из третьего;
![]() из второго, подставив полученное
из второго, подставив полученное
![]()
![]() из первого, подставив полученные
и
.
из первого, подставив полученные
и
.
Таким образом исходная система решена.
СЛАУ имеет несколько решений:
Пусть
![]() —
решения однородной системы ,
—
решения однородной системы ,
![]() —
произвольные константы. Тогда
—
произвольные константы. Тогда
![]() также
является решением рассматриваемой
системы.
также
является решением рассматриваемой
системы.
- Для однородной системы
Теорема
(о структуре общего решения).
Пусть
![]() ,
тогда:
,
тогда:
если
 ,
где
—
число переменных системы, то существует
только тривиальное решение (Нулевое
решение).
,
где
—
число переменных системы, то существует
только тривиальное решение (Нулевое
решение).если
 ,
то существует
,
то существует
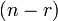 линейно
независимых решений рассматриваемой
системы:
линейно
независимых решений рассматриваемой
системы:
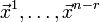 ,
причём её общее решение имеет вид:
,
причём её общее решение имеет вид:
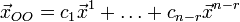 ,
где
,
где
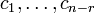 —
некоторые константы.
—
некоторые константы.
- Для неоднородной системы
Теорема (об общем решении неоднородных
систем).
Пусть
![]() тогда:
тогда:
если , где — число переменных системы, то решение существует и оно единственно;
если , то общее решение системы имеет вид
 ,
где
,
где
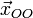 —
общее решение системы, называемое общим
однородным решением,
—
общее решение системы, называемое общим
однородным решением,
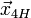 —
частное решение системы, называемое
частным неоднородным решением.
—
частное решение системы, называемое
частным неоднородным решением.
22. Теоре́ма Кро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений: Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.
23. СЛАУ Система m линейных алгебраических уравнений с n неизвестными
в линейной алгебре — это система уравнений вида
|
|
ОСЛАУ Однородной системой линейных алгебраических уравнений называется система вида:
24. Теорема о решении ОСЛАУ Пусть — решения однородной системы (1), — произвольные константы. Тогда также является решением рассматриваемой системы. Теорема (о структуре общего решения). Пусть , тогда:
если , где — число переменных системы, то существует только тривиальное решение;
если , то существует линейно независимых решений рассматриваемой системы: , причём её общее решение имеет вид: , где — некоторые константы.
25. Определение ФСР ОСЛАУ ФУНДАМЕНТАЛЬНАЯ СИСТЕМА РЕШЕНИЙ ОДНОРОДНОЙ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ - Любой базис пространства решений однородной системы линейных уравнений называется фундаментальной системой решений однородной системы. (Базис) - множество таких векторов в векторном пространстве, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого множества— базисных векторов.
